Здравствуйте, меня зовут Дмитрий Карловский. А вы на канале Core Dump, где мы берём различные темы из компьютерной науки и деконструируем их по полочкам.
А на этот раз мы разберём тему "абсурда" — почему он возникает и к каким странным последствиям приводит неосторожное обращение с ним. Докажем, что Санты не существует. Научимся пересчитывать линейки. Остановим временную петлю. И элегантно преодолеем столетний кризис оснований математики.
Так что забирайтесь в кроличью нору — вас ждёт короткое, но увлекательное приключение.
Вы можете либо посмотреть видео запись, либо открыть в интерфейсе проведения презентаций, либо читать как статью...
Классическая логика
Начнём с самых основ. Какие бывают утверждения?
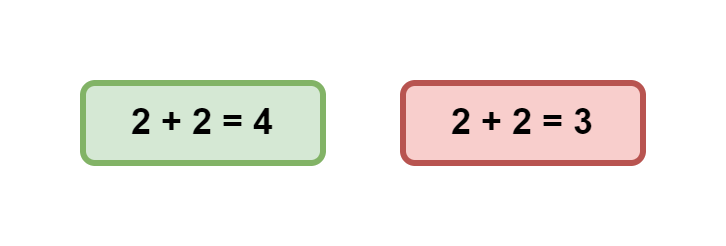
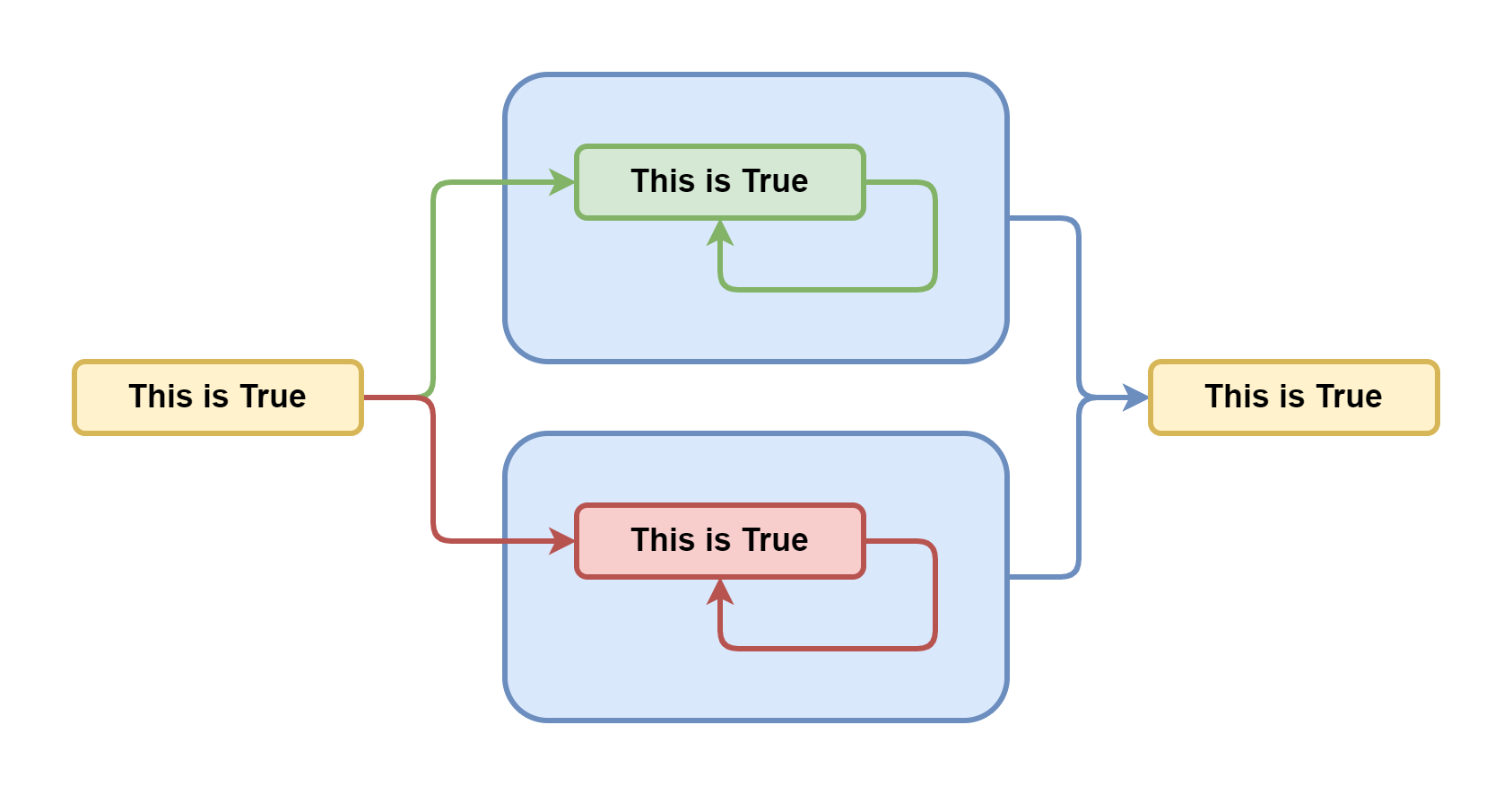
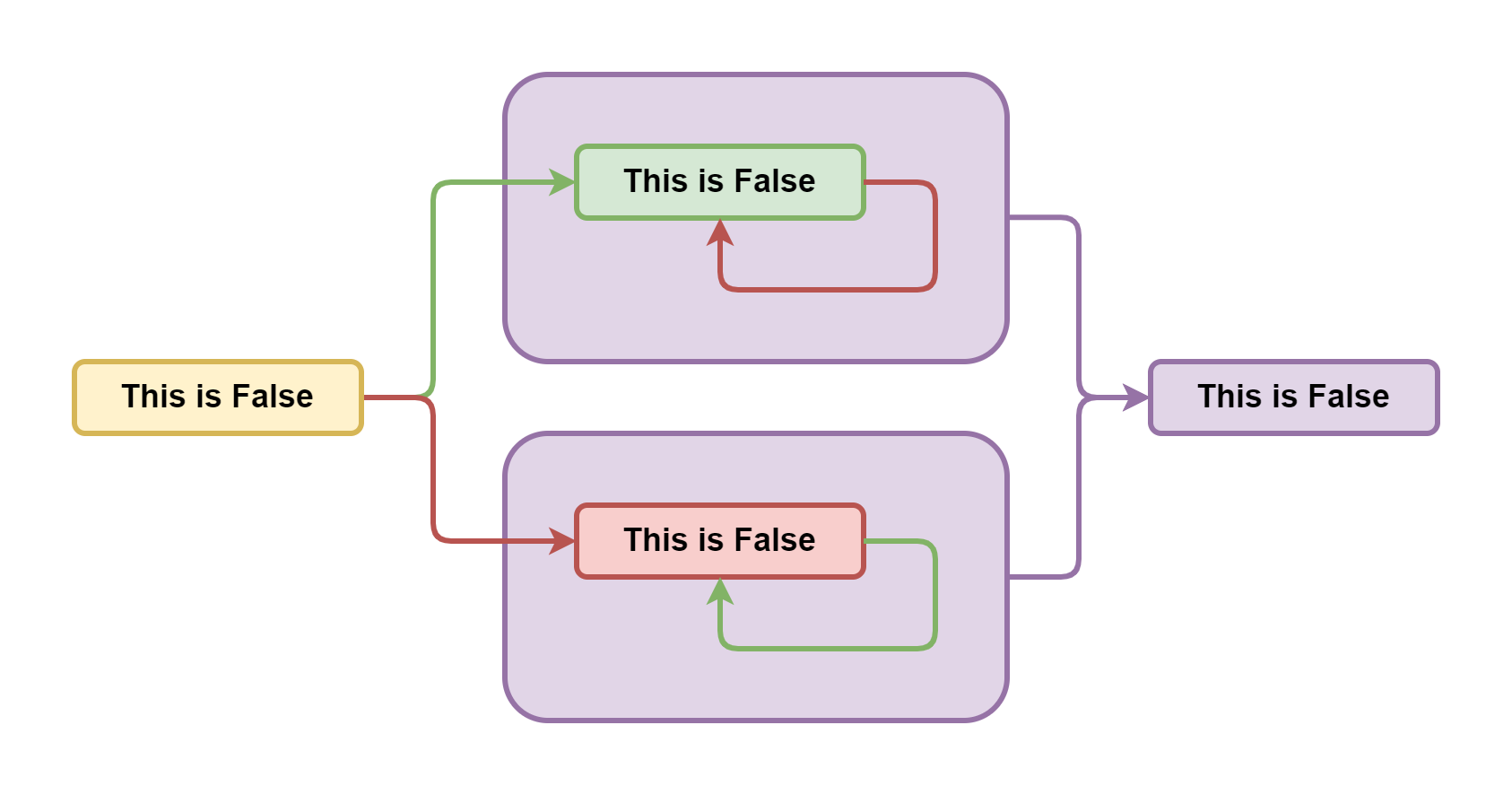
В рамках классической логики они бывают либо правдивыми, либо ложными. Обозначим их соответственно зелёным и красным цветами.
Многозначная логика
Однако, важно понимать, что понятие истинности применимо лишь для корректных утверждений, то есть имеющих какой-то смысл.
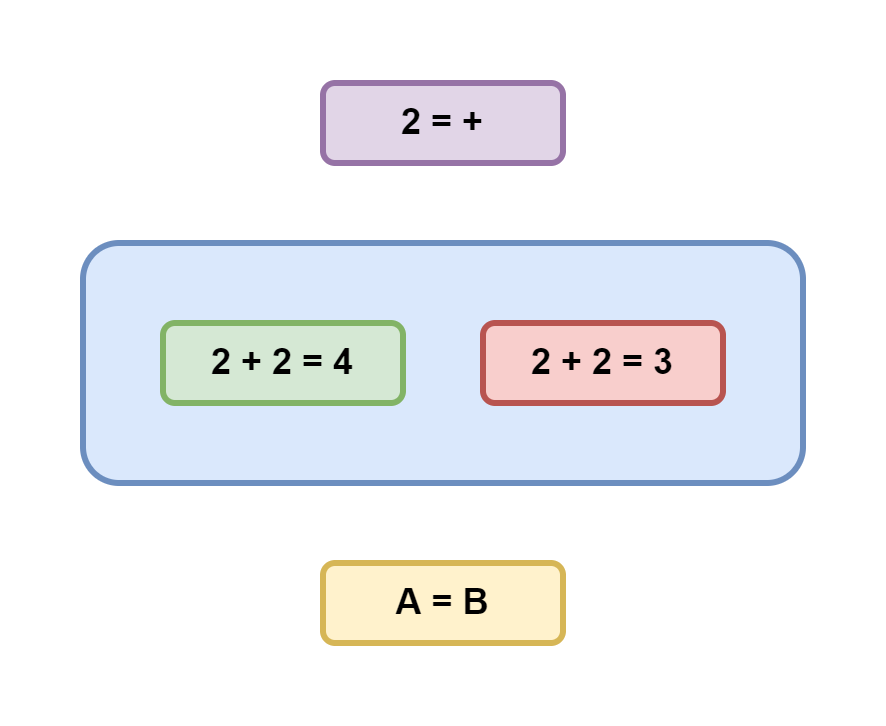
Если же утверждение является не корректным, то оно не может быть ни правдивым, ни ложным. Ведь это бессмыслица, не несущая в себе никакой содержательной информации. Например, можно ли сказать правдиво или ложно выражение 2 = +? Это вообще не понятно что такое. В то же время одинокое высказывание A = B может быть и правдивым, и ложным, но без понимания, что скрывается за A и B невозможно сказать наверняка.
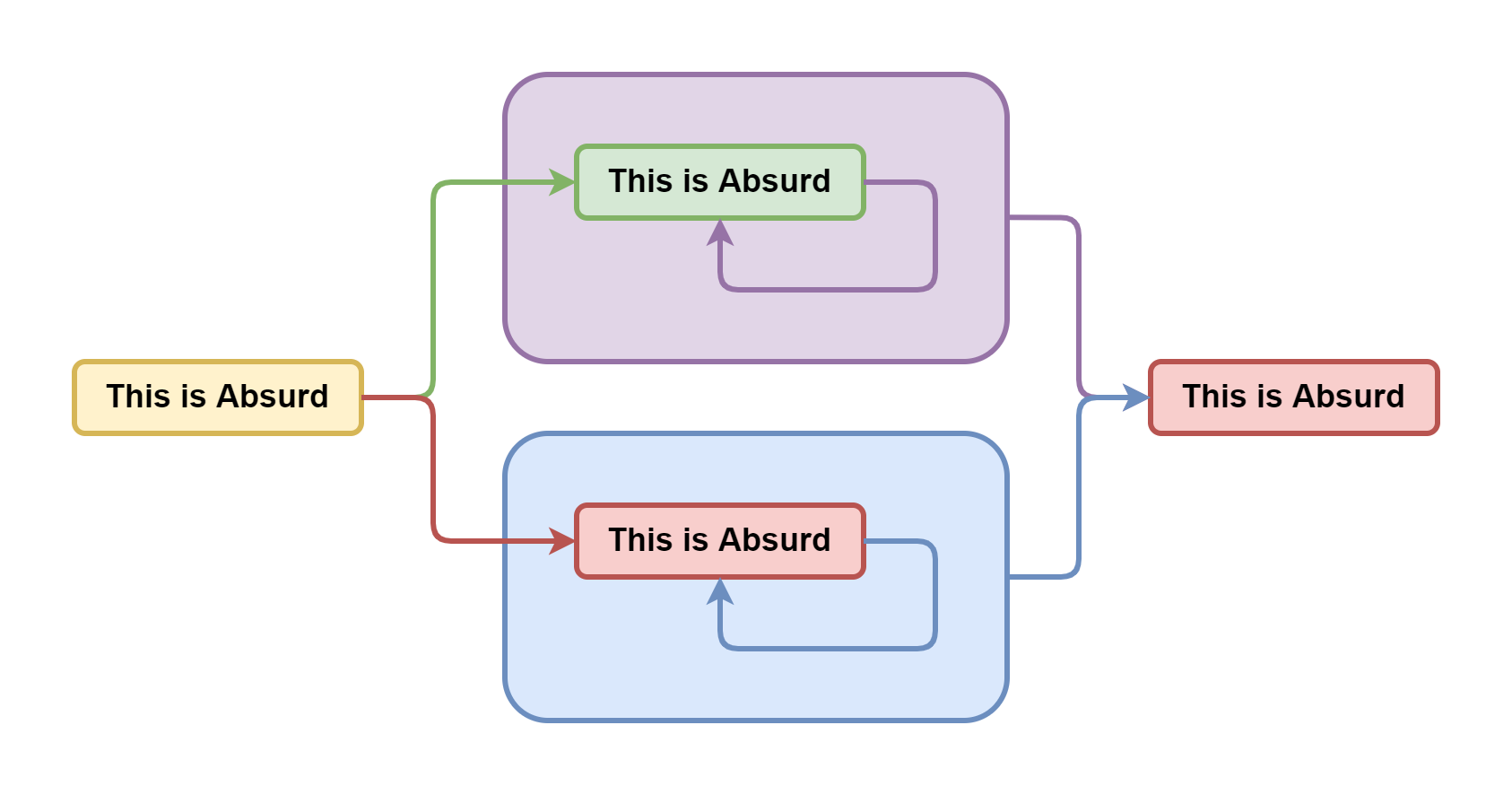
Обозначим корректные утверждения голубым, абсурдные — фиолетовым, а суждения, истинность которых не известна, — жёлтым. Таким образом мы получили так называемую четырёхзначную логику, позволяющую однозначно классифицировать любые типы утверждений исходя из доступной касательно них информации.
Четыре значения истинности
Но почему именно 4 значения нужно, чтобы классифицировать любые утверждения? Дело в том, что это число всех возможных пересечений двух бинарных параметров: может ли утверждение быть правдой и может ли оно быть ложью.
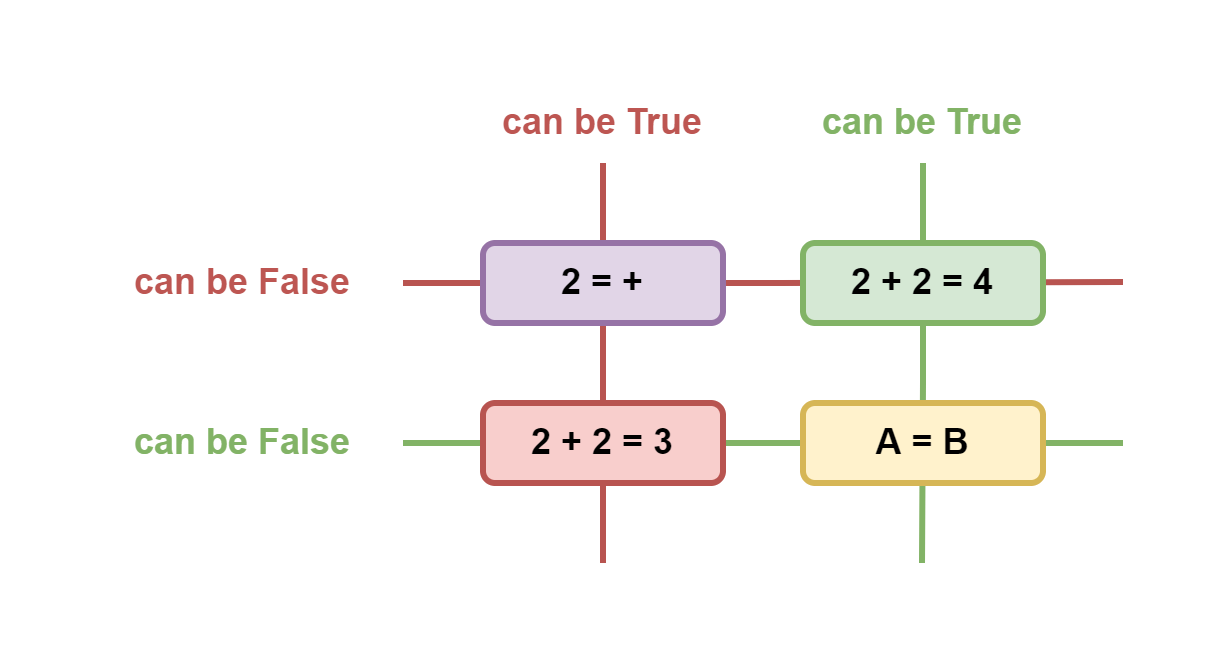
Именно поэтому не бывает, например, пятеричной логики. А вот троичные бывают — они либо удаляют одно из приведённых тут значений из рассмотрения, либо объединяют абсурд и неопределённость в одно значение — "некорректность".
Доведение до абсурда
Давайте рассмотрим, как понятие корректности помогает нам делать логические выводы, на примере популярного в математике метода "доказательства от противного".
Пусть у нас есть уравнение: 2*2 = 2+2. Правдиво оно или ложно?
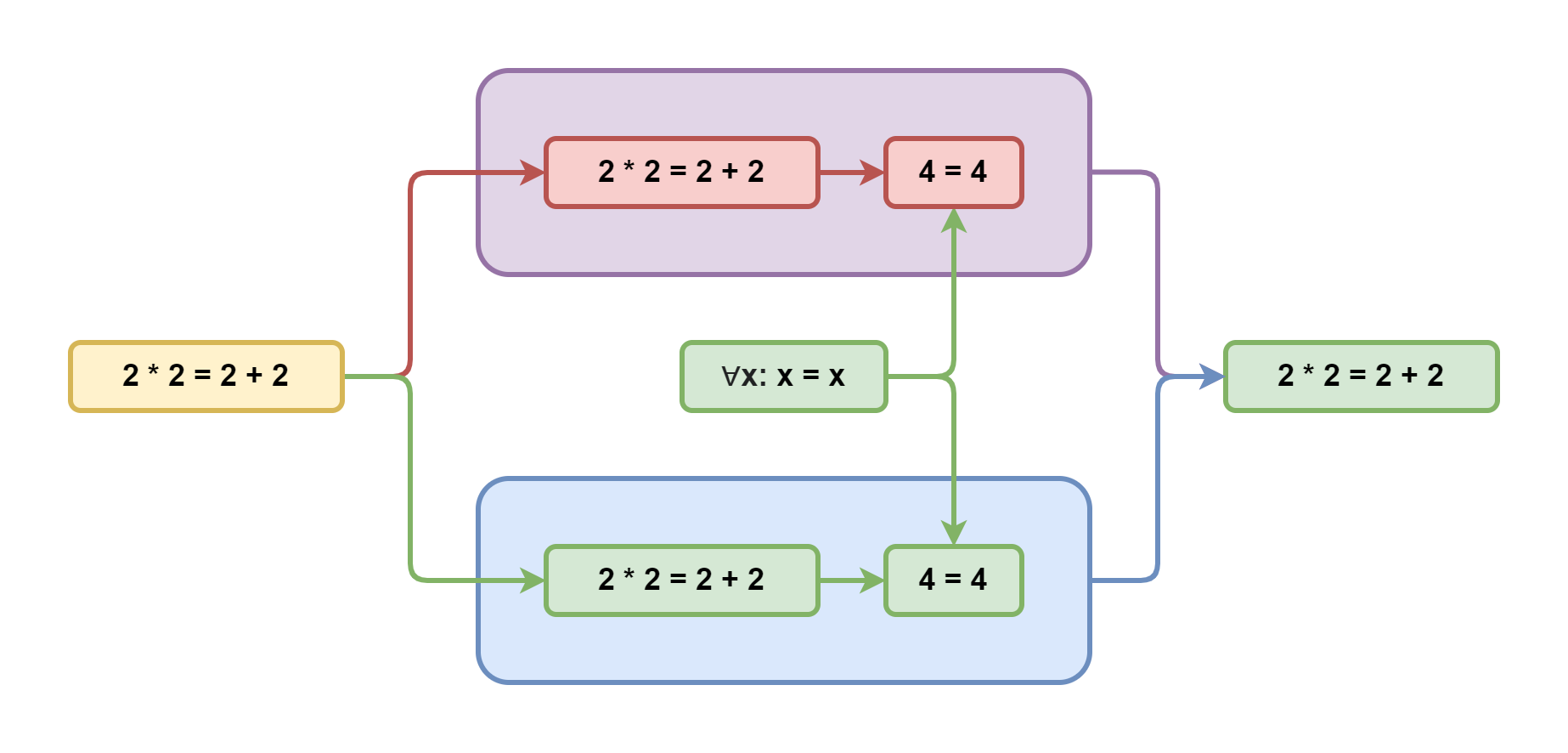
Допустим, что оно ложно. Тогда после вычисления левой и правой частей мы получим, что суждение 4=4 тоже ложно. Однако, у нас есть аксиома тождества утверждающая, что любое число равно самому себе. Получаем противоречие: зелёная стрелка упирается в красный прямоугольник. То есть эта ветка рассуждений абсурдна и поэтому отбрасывается. А значит исходное уравнение не может быть ложным.
Но может ли оно быть правдивым? Что ж, рассмотрим и эту гипотезу. Из неё вытекает, что 4=4 тоже правдиво, что соответствует аксиоме тождества. И никаких противоречий не возникает. А значит эта ветка рассуждений вполне себе корректна. Таким образом мы доказали, что исходное уравнение не может быть ни чем иным, как правдой.
Может показаться, что проверка второй гипотезы уже лишняя, когда опровергнута первая. Ведь если утверждение не ложно, то оно должно быть правдиво. На этот счёт в классической логике даже есть отдельная аксиома "исключённого третьего". Однако, не стоит забывать, что произвольно взятое утверждение может оказаться не только правдивым или ложным, но и попросту некорректным. И в этом случае та аксиома не применима, как и вся классическая логика. Поэтому прежде чем брать такое утверждение в оборот классической логики, необходимо доказать его корректность. Ну либо всё же использовать не классическую, многозначную логику.
Неполнота
Возьмём, для примера, выражение, утверждающее свою собственную правдивость и попробуем его проанализировать.
Если оно правдиво, то оно утверждает, что оно правдиво, что не противоречит исходному предположению. А если оно ложно, утверждая, что оно правдиво, значит оно ложно, что тоже подтверждает исходное предположение. Получается, что это утверждение не несёт в себе достаточно информации, чтобы определить его истинность. А значит его требуется дополнить ещё каким-то суждением, которое бы что-то говорило об истинности данного утверждения.
Конкретно в данном случае нам для полноты не хватает аксиомы, позволяющей установить истинность подобных утверждений. Звучать она может, например, так: выражения, утверждающие свою собственную правдивость, не корректны. Просто потому, что они не дают нам никакой полезной информации для дальнейших рассуждений. Назовём её "аксиомой Мюнхгаузена" в честь известного персонажа, вытаскивавшего самого себя из болота за волосы.
Парадокс лжеца
Но что если утверждение будет говорить о своей собственной ложности?
Если оно правдиво, то из его содержания следует, что оно ложно. Получаем противоречие и отбрасываем. Если же оно ложно, то из отрицания её содержания следует, что оно правдиво. Опять противоречие — снова выбрасываем.
Получается, что такое утверждение противоречиво само по себе, а значит некорректно. Оно не может быть ни правдой, ни ложью, независимо от любых других суждений. Такое утверждение является семантической бессмыслицей, также известной как "парадокс лжеца". И из неё нельзя сделать никаких содержательных выводов, кроме того, что оно абсурдно.
Это — абсурд
Может показаться, что мы не разрешили парадокс, а лишь убежали от него. И если заменить ложность на абсурдность, то парадокс вернётся вновь. Но давайте рассмотрим и выражение "это утверждение абсурдно".
Из его правдивости следует его же абсурдность, что является абсурдом. Однако, из его ложности следует его корректность, что не вызывает противоречий. Получается, что оно вполне корректно, но ложно. И никаких парадоксов не возникает.
Первая теорема Гёделя о неполноте
Ладно, давайте разберём что-то по сложнее. Например, первую теорему Гёделя о неполноте. Суть её сводится к тому, что в любой непротиворечивой системе утверждений существует такое правдивое утверждение, которое невозможно доказать. То есть эта система не полна. Для обоснования приводится выражение вида "это выражение невозможно доказать". Давайте проанализируем его, как мы умеем..
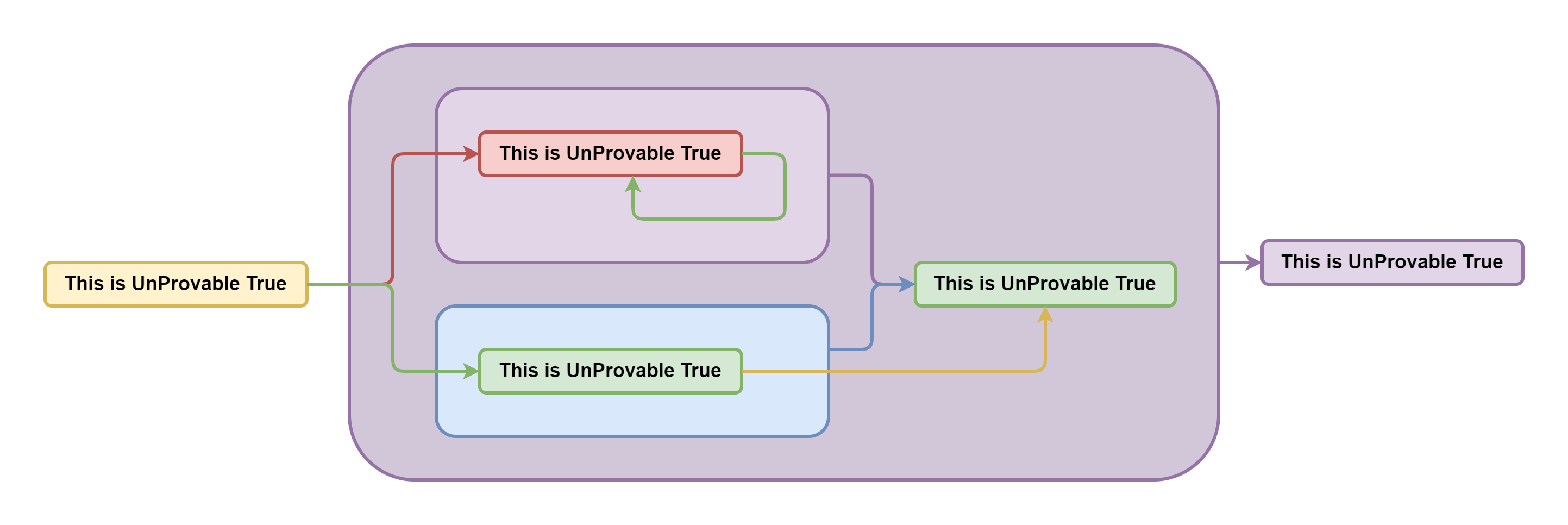
Если оно ложно, значит доказать его всё же можно. А если можно доказать, то оно правдиво. Противоречие — отбрасываем. Если же оно правдиво и непротиворечиво, а ложность мы уже отвергли, то получается, что мы его доказали. А оно говорит о своей недоказуемости. Опять противоречие — снова отбрасываем. А так как мы только что доказали, что оно не может быть ни правдивым, ни ложным, значит оно абсурдно.
Тут Гёдель заявляет, что мы же не смогли доказать утверждение, которое говорит о своей собственной недоказуемости, что получается правда и теорема как бы доказана. Однако, тут важно помнить, что невозможность правдивости мы уже только что показали. А суть тут в том, что понятие истинности (и как следствие доказуемости) в принципе не применимо к абсурдным утверждениям.
Это всё равно, что спрашивать "Когда вы перестали пить по утрам?" у человека, который в жизни в рот не брал. По сути, выражение Гёделя — не более чем слегка завуалированный парадокс лжеца, где утверждение эффективно отрицает само себя. Важный вывод из этих рассуждений заключается в том, что введение в рассуждение абсурдного утверждения не поможет ничего доказать или опровергнуть, кроме собственно абсурдности этого утверждения.
Вторая теорема Гёделя о неполноте
У того же Гёделя есть и другая теорема, утверждающая, что в любой непротиворечивой системе утверждений недоказуемо утверждение о её непротиворечивости. Для "доказательства" он использует то же самое абсурдное утверждение, которое мы разобрали ранее. Поэтому, вместо очередного опровержения некорректных рассуждений, давайте просто докажем утверждение о собственной непротиворечивости...
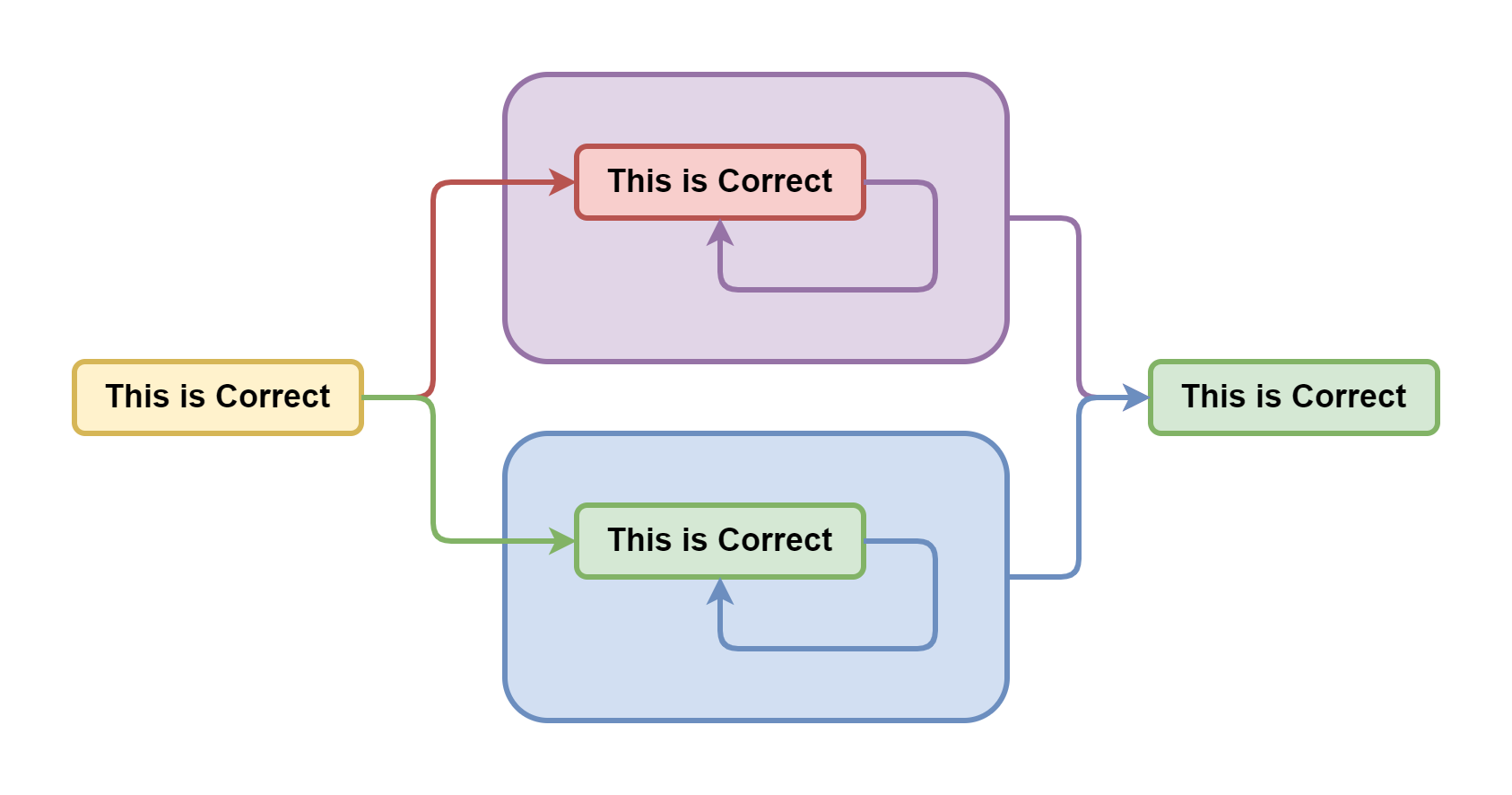
Если утверждение "эта система утверждений корректна" ложно, то система утверждений не корректна, то есть противоречива. Если же это утверждение — правда, то система утверждений корректна, что не вызывает противоречий. Соответственно это утверждение не может быть ни чем иным как правдой.
Получается, что четырёхзначная логика, в отличие от классической, позволяет строить непротиворечивую, но при этом полную систему утверждений, позволяющую использовать её в качестве фундамента для математики. Ведь она позволяет однозначно выводить одно из четырёх возможных логических значений. А теоремы Гёделя просто показывают несостоятельность классической логики.
Разбиение множества по предикату
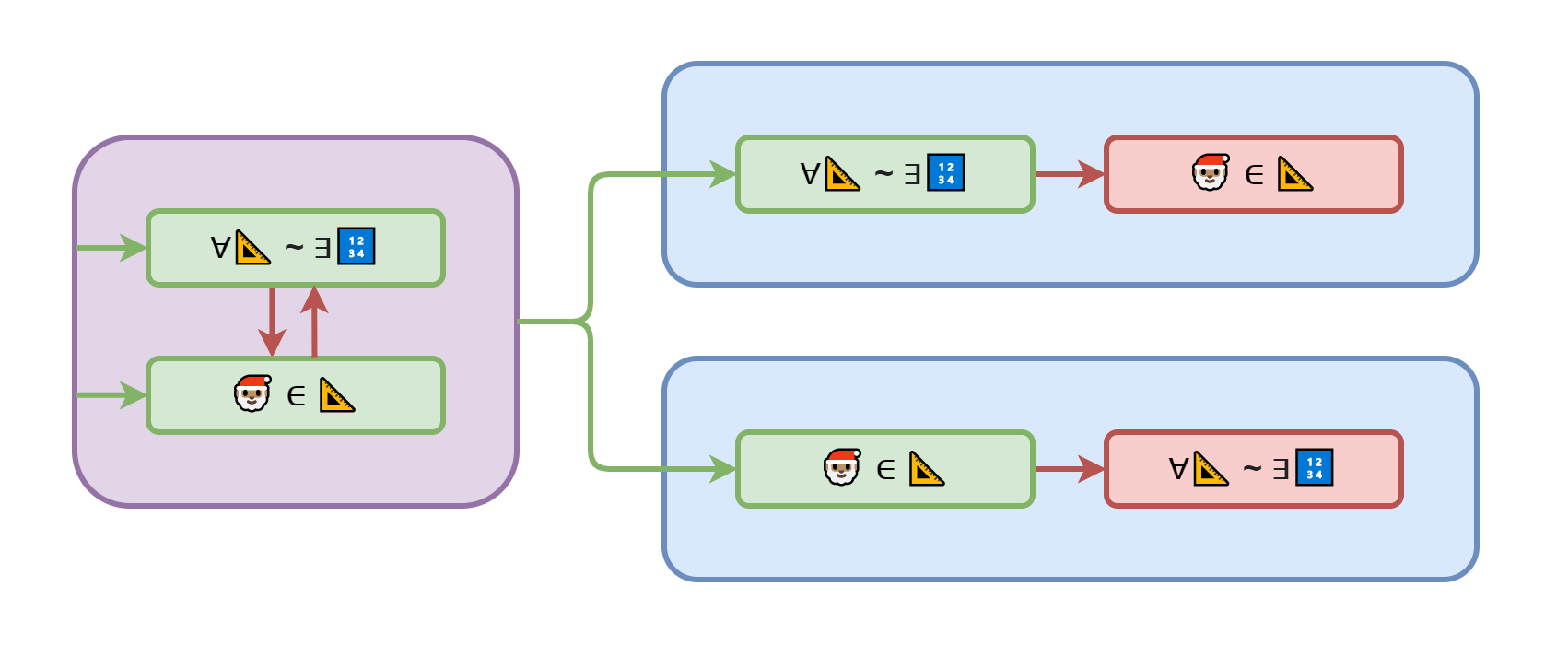
Поднимемся на уровень выше, к теории множеств, где мы можем образовывать подмножества используя произвольный предикат, то есть функцию, которая возвращает правду или ложь. Возьмём, например, предикат "стрижёт" и разделим всё население Земли на тех кто стрижёт сам себя и тех, кого стригут другие. Первых обозначим бритой рожицей так как они могут себе позволить стричься хоть каждый день. А вторых — заросшей, так как для них сходить к цирюльнику — это целая эпопея.
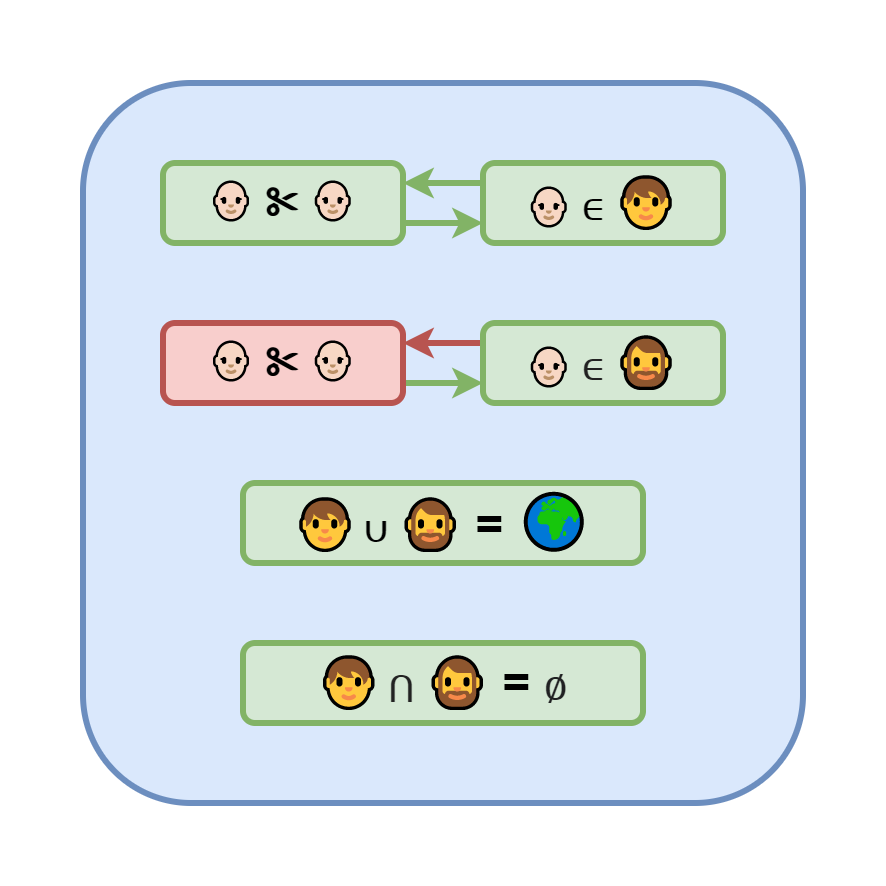
Так как мы разделили всё население по предикату на два подмножества, то так же верны и утверждения, что объединение этих подмножеств равно всему населению планеты. А пересечение является пустым множеством, ибо никто не может и стричь себя сам, и не стричь одновременно.
Введение определений
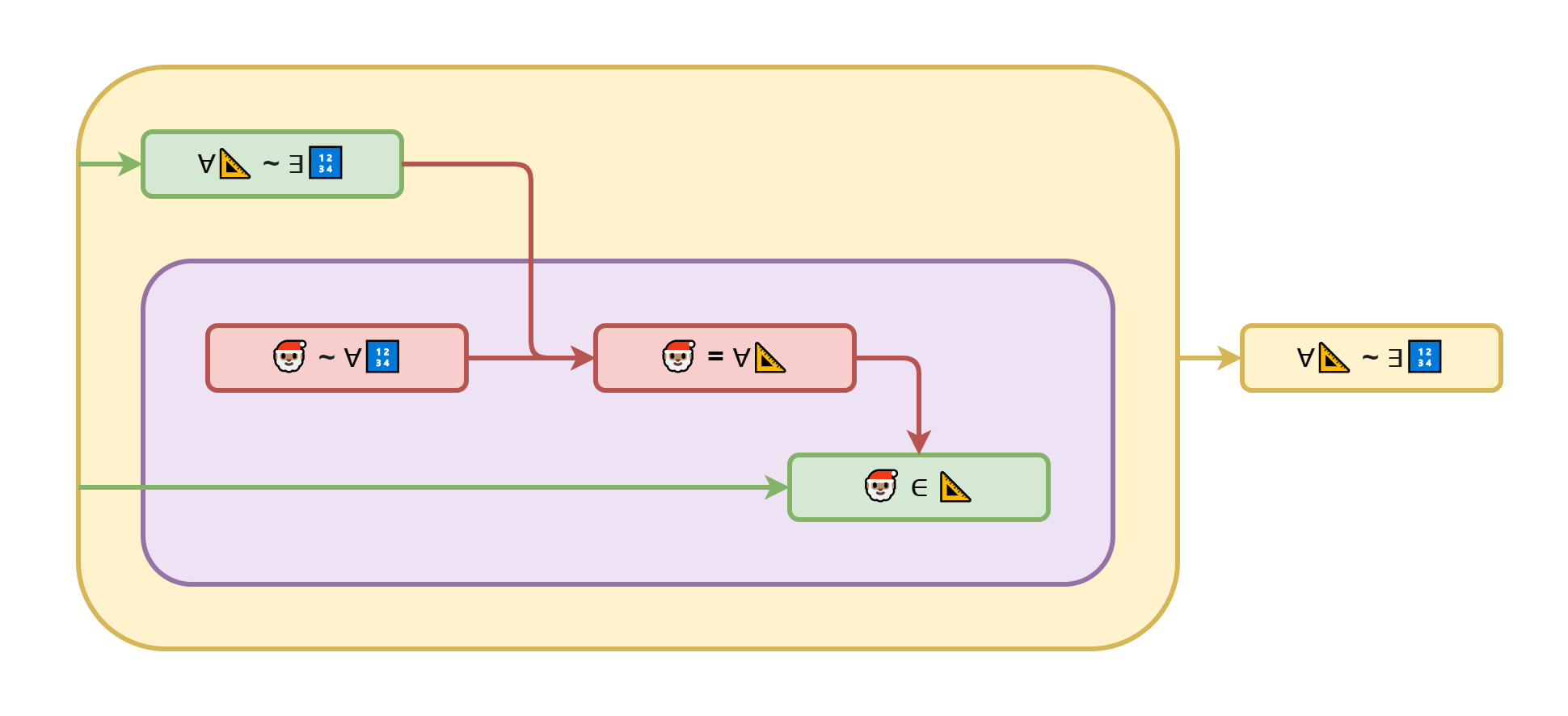
Теперь давайте представим себе такого персонажа, который стрижёт всех и только тех жителей, кто не стригут себя сами. Назовём его Сантой и формализуем его определение в виде системы из 3 утверждений..

Сначала мы утверждаем, что он принадлежит множеству населения Земли. Потом, что он стрижёт любого землянина, что не стрижёт себя сам. И наконец, он не стрижёт никого из тех, кто и сам себя не прочь постричь.
Но что за дела? Почему определение завёрнуто в жёлтый прямоугольник неопределённости? Как же так?
Парадокс брадобрея
Дело в том, что прежде чем вводить в рассуждения новое определение, необходимо доказать, что оно корректно, то есть описывает то, что действительно может существовать, а не является абсурдом. Давайте попробуем это сделать..
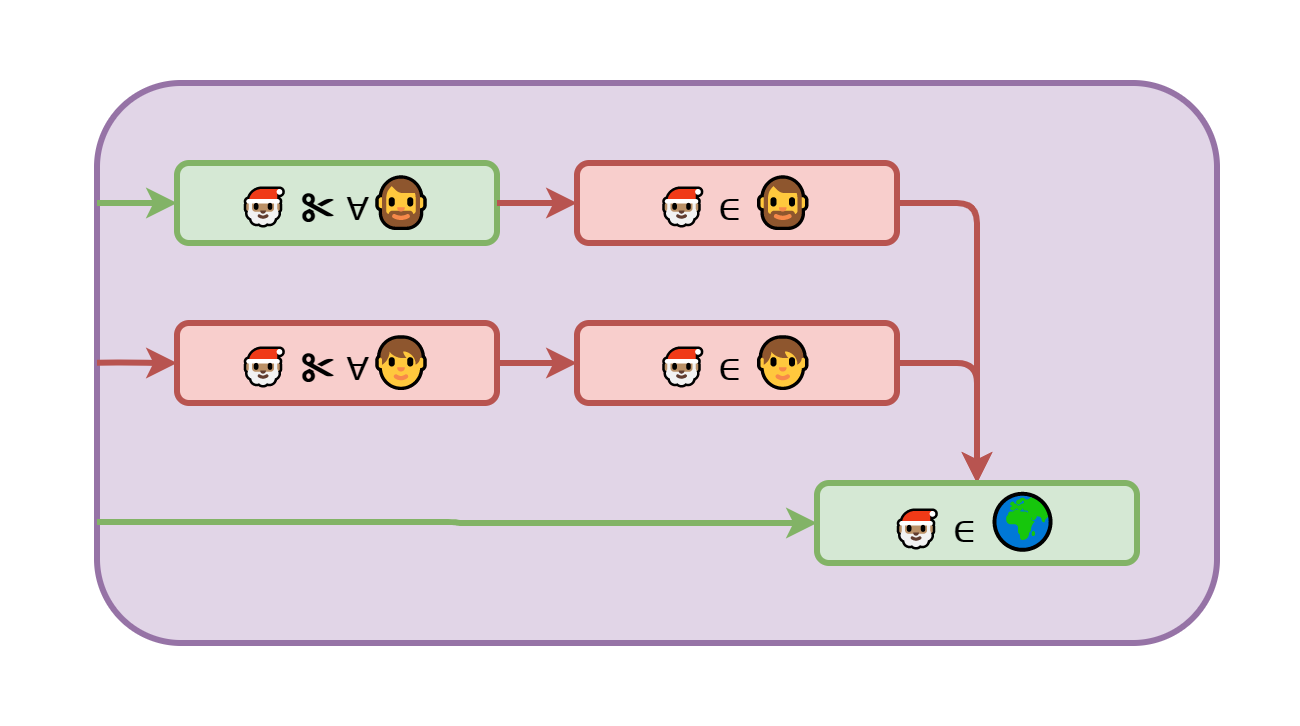
Если любого, кто не стрижёт себя сам, стрижёт Санта, то сам Санта не может входить в это множество ибо тогда Санте пришлось бы стричь самого себя. С другой стороны, раз он не стрижёт никого из самостригущихся, значит сам он тоже не принадлежит к самостригущимся. Объединяя оба вывода, получаем, что… Санты не существует, как это ни печально. Однако, он должен существовать исходя из нашего определения.
Получается, что система из 3 утверждений входящих в определение Санты противоречиво само по себе и не может использоваться для введения такой сущности в рассуждения. Такое абсурдное определение называется "парадоксом брадобрея" и имеет множество различных вариаций. А важный вывод из него заключается в том, что не всё, что можно описать может действительно существовать. Поэтому вводя новые сущности всякий раз необходимо доказывать непротиворечивость их описания.
Несчётные множества
Давайте подумаем, что будет, если мы не будем отвергать абсурдные определения. Для этого рассмотрим теорему Кантора о несчётности вещественных чисел. Для наглядности, обозначим множество вещественных чисел как линейку, а множество натуральных как циферки в квадрате.
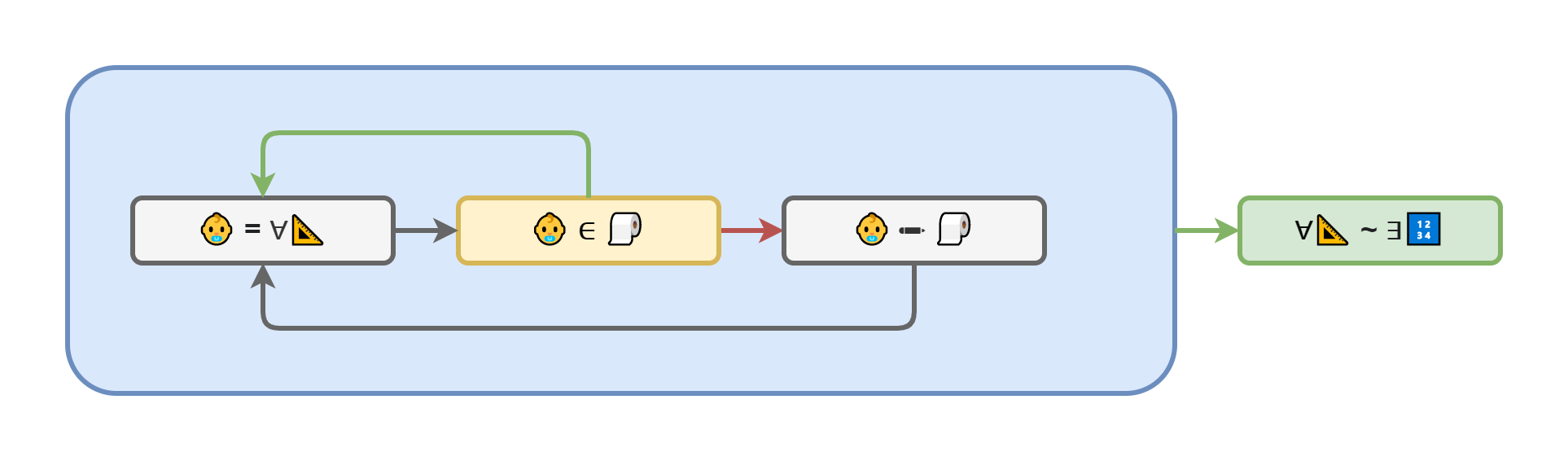
Вкратце, доказательство Кантора выглядит так: предположим, что для любого вещественного числа существует соответствующее ему уникальное натуральное число. Теперь введём в рассмотрение Санту — некоторое вещественное число, которое по построению не соответствует ни одному натуральному. А в рамках исходной гипотезы, в которой мы не сомневаемся, пока она не опровергнута, его определение эквивалентно следующему: "Санта — это такое вещественное число, которое не равно… никакому вещественному числу".
Получается, что Санта сам не может быть вещественным числом. Однако, ранее мы постулировали, что такой Санта среди вещественных чисел есть. И тем самым, кстати, нарушили один из основных принципов доказательства от противного — недоказуемая посылка в нём может быть только одна — которая далее и опровергается. А в "доказательстве" Кантора их две — одна явная, а другая не очень.
Направления математики
Получившееся противоречие означает, что невозможно одновременное существование Санты и соответствия между нашими множествами. Чтобы его разрешить, можно, например, признать, что такой самоотрицающий себя Санта существовать не может, а значит множество вещественных чисел счётно и все бесконечности равны.
Ну а можно заявить, что если мы смогли Санту описать, значит он существует. А следовательно не существует соответствия, и одна безконечность, внезапно, может быть больше другой безконечности. Как минимум на один элемент. А это открывает широкие горизонты для целого математического направления с ординалами, кардиналами и прочими классами. Именно так и поступил Кантор, а вслед за ним и вся формалистская школа математики, породив тем самым несчётное множество парадоксов.
Отмечу, однако, почему это тупиковый вектор развития. В окружающем нас мире всё конечно. Поэтому алгебра бесконечностей принципиально бесполезна с практической точки зрения. Так что её можно безболезненно удалить бритвой Оккама и получить стройную непротиворечивую математику не опирающуюся на абсурдные сущности.
Пересчитываем действительные числа
Ну ок, мы показали, что вещественные числа пересчитать всё же можно. Но как именно это сделать? Давайте сформулируем самый простой алгоритм..
Возьмём пустой ряд вещественных чисел и начнём заполнять его так: берём случайное вещественное число и проверяем есть ли оно уже в нашем ряду. Если оно уже есть — генерируем новое. И так далее, пока не встретим число, которое ещё не посчитали. Добавляем его в конец ряда и всё по новой.
Понятно, что для произвольного вещественного числа вероятность получить именно его на очередной итерации бесконечно мала. Но так как у нас есть неограниченное число попыток, то математическое ожидание, что оно нам попадётся в ряду хотя бы раз, равно единице. А это значит, что для каждого вещественного числа неизбежно будет получен уникальный натуральный номер в ряду. А следовательно, все бесконечные множества равны между собой по своей мощности.
Проблема останова
Наконец, мы добрались до проблемы останова. Суть её заключается в том, чтобы написать такой анализатор, который бы для любого алгоритма мог сказать завершится тот когда-нибудь или же будет исполняться бесконечно долго. Сотню лет назад Алан Тьюринг доказал невозможность существования такого алгоритма. И я думаю вы уже понимаете каким вымышленным персонажем он для этого воспользовался.
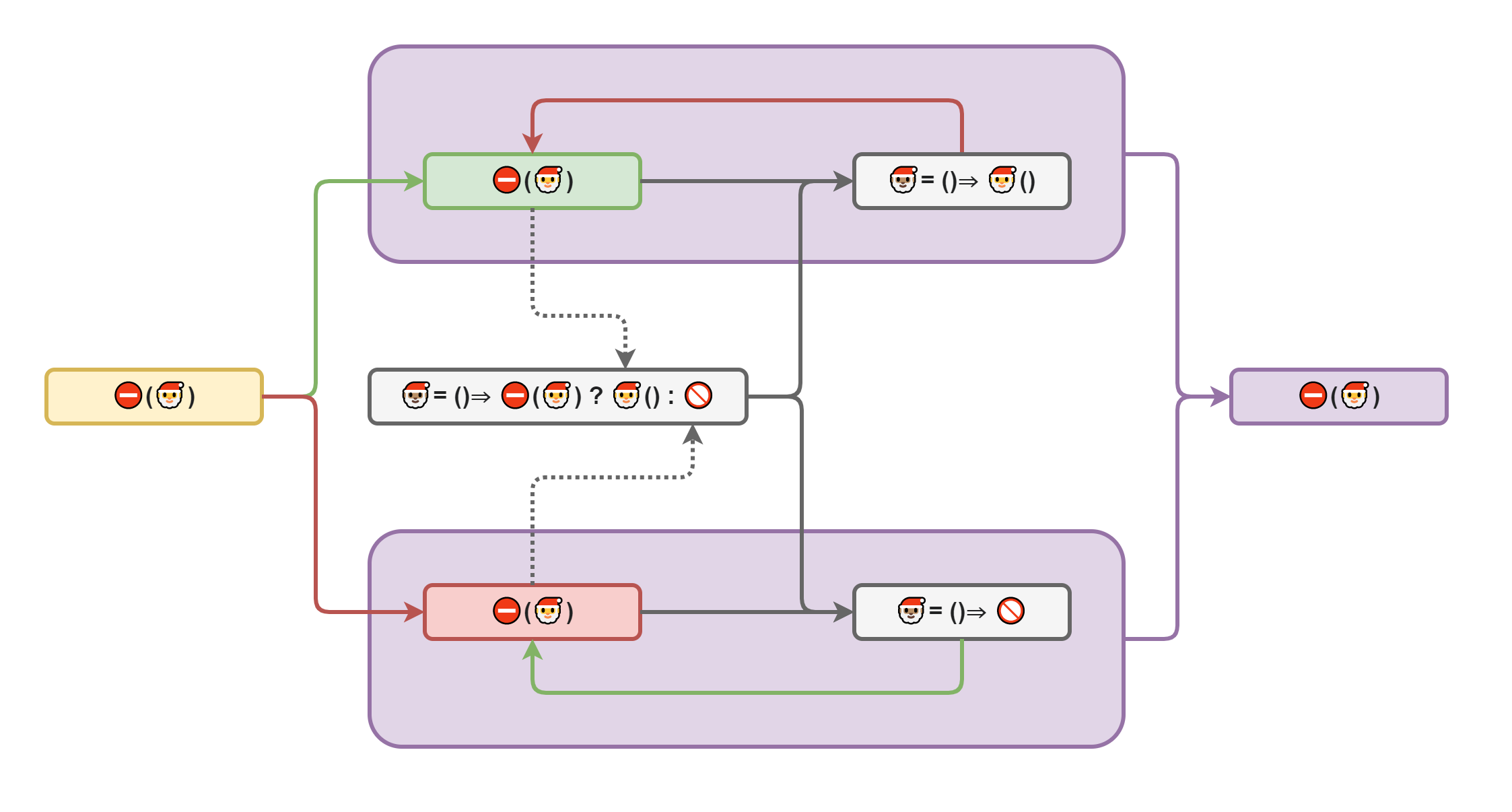
Итак, предположим, что такой анализатор существует и обозначим его знаком "стоп". Он принимает произвольный алгоритм и возвращает флаг истинности. Теперь напишем нашего Санту таким образом, что он вызывает анализатор на самом себе и поступает ровно противоположно его решению: уходит в бесконечную рекурсию, если анализатор говорит, что алгоритм останавливается, но успешно завершается, если анализатор говорит, что остановки не произойдёт.
Понятное дело, что анализатор на таком алгоритме не сможет вернуть ни правду, ни ложь, так как Санта сформулирован в форме абсурда. Значит такого анализатора не существует? Да нет же, существовать он может, но должен бросить ошибку, так же как и для любого другого некорректного кода. В данном же случае текст ошибки может быть примерно такой: "алгоритм не корректен, так как его поведение зависит от результата работы анализатора".
По сути, рассуждения Тьюринга говорят нам не о том, что анализатора быть не может, а то, что классической (бинарной) логики не достаточно для представления результата его работы — нужна как минимум троичная, в которой представим в том числе и вердикт о некорректности кода.
Проверка останова
Что ж, сформулируем простейший и максимально неэффективный анализатор останова. Для начала возьмём некоторый конечный объём памяти и заметим, что число возможных состояний этой памяти тоже конечно. А так как работа исполнителя целиком и полностью определяется состоянием памяти, то он неизбежно за конечное время придёт либо в терминирующее состояние, либо в одно из состояний, в котором он уже был, и соответственно пойдёт по уже проложенному пути и будет делать так бесконечно долго.

Получается, всё, что нам нужно сделать — это исполнить алгоритм, на каждом шаге запоминая полное состояние памяти и сравнивая его со всеми предыдущими состояниями. Как только состояния совпадут — говорим, что алгоритм не останавливается.
Однако, машина Тьюринга, в отличие от любой реальной машины, обладает бесконечным объёмом памяти, что не позволяет вот так вот в лоб за конечное время проверить остановимость алгоритма. Тут уже потребуется анализ потока исполнения для ответа на вопрос: "окажется ли указатель исполнителя за пределами произвольно заданного диапазона памяти". Если ответ утвердительный, то по индукции следует, что алгоритм никогда не остановится. Если же отрицательный, то задача сводится к варианту с конечной памятью.
Можно ли написать такой анализатор, определяющий выход за границы памяти, — вопрос хороший и ответа на него у меня сейчас нет. Возможно именно вы сможете на него ответить? Только чур не ссылаться на Санту!
Резюме
На этом мы пока что остановимся и резюмируем сделанные выводы..
- Самоотрицание не продуктивно.
- Через абсурд ничего не доказать.
- Классическая логика ограничена.
- Четырёхзначная логика лишена парадоксов.
- Все бесконечности равны.
- Проверить остановку — не проблема.
- Математика свернула не туда.
Самоотрицание само по себе не позволяет что-либо доказать или опровергнуть. Оно лишь показывает ограниченность классической логики, не позволяющей оперировать абсурдными утверждениями. А вот четырёхзначная логика позволяет. Так что в ней логические парадоксы в принципе не возникают, что делает её отличным кандидатом для непротиворечивого, но при этом полноценного фундамента математики, где все бесконечности равны, любое утверждение можно вывести, а любой алгоритм можно проанализировать. Но, к сожалению, математика как свернула не туда, так там до сих пор и буксует.
Чтиво по теме
И тут вы, возможно, спросите меня: "Ты что тут самый умный что ли? Математики думаешь всё это не продумали? Иди книжки почитай!". И тут я с вами соглашусь. Чтобы глубоко понять проблематику нужно ознакомиться с её рассмотрением с разных сторон. А не только лишь с одной, господствующей на данный момент, школой математики. Ведь она не единственная. И математики до сих пор не пришли к консенсусу. Предпочитая скорее прятаться от проблем классической логики, чем решать их. Поэтому могу порекомендовать следующие материалы по теме..
- Ошибка Георга Кантора / Зенкин АА
- Логика с операторами истинности и ложности / Павлов СА
- Теория множеств: логика, формализм и кризис / Макар Светлый
В работе Зенкина теорема Кантора рассматривается с несколько иных позиций, но результат такой же для неё плачевный. В работе Павлова подробно разбирается четырёхзначная логика и её соотнесение с классической и другими близкими типами логик. А в обзоре Макара Светлого вы можете проследить всю историю кризисов оснований математики.
Продолжение следует..
Лайк
Подписка
Комментарий
Поделись-ка
Что ж. Пишите в комментариях, как сильно я не прав. Ставьте лайк, если хотите добавки. Подписывайтесь на канал, чтобы её не пропустить. И конечно же, делитесь ссылкой со знакомыми математиками, пусть они тоже поугарают.
А на этом пока что всё. С вами был абсурдный программер Дмитрий Карловский.


Alexufo
Был у меня в детстве знакомый хакер, сильно похож на Орландо Блума, пришлось менять ему профиль деятельности, к нему даже с телевидения приезжали, ну не смог он оставаться в тени. Я ни на что не намекаю, но… не удержался)
nin-jin Автор
Я типа на Блума похож или на этого ведущего?
Alexufo
Ну какой Блум) на Джимми Фелтона.
Джимми
У каждого свои ассоциативные ряды, у меня вот такие.
aamonster
Хорошо написано… Но фигня.
Взять хотя бы проблему останова.
С каким именно диапазоном надо работать? Мы задаём его заранее или мы должны проверить на 10 ячейках, на 100, на 1000 и так далее… И где остановиться?
nin-jin Автор
Диапазон — свободная переменная. Задача анализатора понять, что какой бы диапазон мы ни задали — указатель из него выйдет. Я это не уточнил, но благодаря индукции ему доступна информация о том, что объёма памяти на 1 бит меньше уже не хватает.
aamonster
Вот "понять, что какой бы диапазон мы ни задали — указатель из него выйдет" требует неизвестного времени. Может статься, это время будет линейно расти с увеличением размера диапазона. А может, даже экспоненциально. Т.е. ограничить время, не зная заранее размер диапазона, никак.
Детальнее можете изучить, читая про гипервычисления https://en.m.wikipedia.org/wiki/Hypercomputation и далее по ссылкам.
nin-jin Автор
Похоже вы не до конца понимаете суть квантора всеобщности (?). Вывод делается для всех диапазонов сразу, а не для какого-то конкретного. Достаточно иметь возможность за конечное время доказать индукционный переход.
aamonster
Я? А может, вы?
С чего вы взяли, что индукционный переход доказывается за конечное время? (в данном случае, очевидно, не доказывается)
CrazyOpossum
Забыли проверить утверждение «Это утверждение Жёлтое (истинность зависит от контекста)».
Охх.
Какая вторая? Что «Пусть такой Санта существует»? Ну так он конструктивно получается по нашему соответствию «вещественные -> натуральные». Пусть есть инъективная «f: R -> N», упорядочим вещественные числа по их образу, рассмотрим двоичное представление, построим число, у которого n-ая цифра после запятой равна отрицанию n-ой цифры после запятой n-го числа. Вот и Санта.
Оракул, который принимает любой алгоритм на вход и бросает на выход ошибку формально подходит под ваш критерий, но не даёт никакой информации.
яснопонятно
Какое-то дикое извращение интуиционистской логики с попутным отрицанием Кантора, Гёделя и Тьюринга и замахом на безупречную матлогику.
nin-jin Автор
Без дополнительных утверждений это неопределённость.
Не получается. Исходя из первой гипотезы любое вещественное число, как бы мы его ни генерировали, уже будет иметь прообраз. А канторово число — не более, чем попытка угнаться за хвостом, так же как и в случае с 0.(9), который эффективно равен 1.
Раз уж вас триггерит теорема Кантора, то можете подумать ещё и вот над чем: если разделить множество действительных чисел на счётное подмножество и его дополнение, то теорема кантора фактически "доказывает", что в дополнении можно найти хотя бы 1 число. Однако, не сложно показать, что существует отображение счётного множества на счётное множество, дополненное 1 элементом. То есть для доказательства несчётности необходимо не просто доказать, что мощность дополнения не меньше 1 и даже не достаточно доказать, что его мощность счётна. Нужно доказать, что мощность дополнения более чем счётна. Получаем порочный круг — чтобы доказать несчётность одного множества, нужно доказать несчётность его подмножества. Уроборос.
Он даёт некорректный ответ, так как исполнитель сможет исполнить алгоритм, который не зависит от оракула.
CrazyOpossum
Именно это оно и утверждает, а следовательно истинно. Раз уж на то пошло, как выглядит исчисление высказываний в вашей логике? Как выглядят матрицы для конъюнкции и импликации? Какой цвет у «Из фиолетового следует зелёный»?
Вещественное пространство по определению полно — к чему бы мы не гнались, это последовательность с конкретным пределом. Этот предел — вещественное число и не имеет образа. Последовательность 0.9, 0.99, 0.999… так же стремится к 1, а 3, 3.1, 3.14, 3.141… — к пи.
Тут стрелочки в разные стороны смотрят. Это совершенно нормально, что по следствиям теоремы нельзя пройти в обратном порядке и получить доказательство теоремы.
Как мы делим алгоритмы, для которых допустимо кидать ошибку или нужно обязательно дать ответ остановится или нет?
nin-jin Автор
Если жёлтый — это неопределённый, то абсурд получается:

В статье есть ссылка на книгу, где вы найдёте все ответы.
Фиолетовый, ибо я не смог это выражение интерпретировать.
Обратите внимание, что каждый бит этих двух записей одного числа попарно отличается.
Доказательство опирающееся на собственное доказательство — это не нормально.
Странный вопрос. Видим ошибку — кидаем. Не видим — не кидаем.
CrazyOpossum
Не показатель. Хорошо, сделаем так. Пусть мы отобразили все вещественные числа в натуральные, пронумеруем образы по возрастанию, получили новое отображение в [1..], будем работать с ним. Рассмотрим число, равное
F^{-1}(n) — прообраз n. Я не пользуюсь представлением числа вообще. Эта последовательность фундаментальна, так как разница между соседними членами не больше чем 1/2^n, следовательно сходится в R. Если некоторому F(x) = k, то 0 = x — x = 1/2^k.
В каком месте доказательства выше используется разность множеств?
Из «алгоритм существует» следует ли что «алгоритм корректен»? Если да, тогда корректен ли тот же алгоритм + отрицание? Что вернёт такой алгоритм при применении на себя?
nin-jin Автор
Мне не знакома эта нотация.
Анализатор Тьюринга проверяет не просто алгоритм, а алгоритм с конкретными аргументами вызова. И вот эта комбинация алгоритм+аргумент не корректна.
CrazyOpossum
Прочитал статью Зенкина — его опровержение это «Вот Кантор предполагает что из функции [ F => -F ], но я рассмотрел F под другим углом и получил что из [ F' => -F ], что совсем даже неплохо». Увы, так не работает и Кантор так не говорил.
nin-jin Автор
К сожалению, вы ничего не поняли в статье Зенкина. Бывает.
ilynxy
Например, бывает. Бывают многозначные логики. И даже бесконечнозначные. И успешно используются.
Ну так эт, ждём
ebuildпрорывов.nin-jin Автор
Вероятностный метод смотрит на Цермелло-Френкеля в недоумении.
Это уже нечёткая логика. И это большой вопрос можно ли называть её логикой вообще.
ilynxy
nin-jin Автор
Это два не пересекающихся раздела математики. Да и аксиома выбора не про выбор одного элемента из множества, а про населённость декартова произведения семейств множеств.
netricks
Хотя понятно, что в условиях ограниченного числа ячеек памяти алгоритм или свалится с ошибкой выхода за диапазон, или зациклится, практической ценности рассмотрение такого ограничения не имеет, поскольку количество возможных состояний с ростом числа ячеек возрастает экспоненциально. Можно создать нетривиальный алгоритм, который будет очень долго перекладывать байтики и никогда не повторится. А еще у него будет хитрое и почти невероятное условие, по которому он завершит вычисление. Для каких-то частных случаев останов можно будет предсказать, но в общем случае нет. Такой алгоритм бесконечность считать не будет, но срок времени близкий к времени существования вселенной — запросто. В качестве примера — взлом какого-нибудь криптостойкого кода в условиях, когда неочевидно, что закодированная информация вообще осмысленна.
Понятно, что остановится… А вот, когда — шут знает...
technic93
Начал читать и сразу вопрос: Почему желтые утверждения (истинность которых неизвестна) не являются корректными (т.е. голубыми)? Судя по картинкам это так.
nin-jin Автор
Они не корректные лишь с точки зрения классической логики, где никаких неопределённостей быть не может.
technic93
Ну вот "2 = +" это синтактический мусор, а "A = B" это вроде бы ок (при условии что А и B тоже синтаксически коректны). Почему оно не в голубом множестве на одной из первых картинок?
Апд. Наверное надо добавить ещё какой-то цвет, это те утверждения про которые мы ещё не думали. Потому что иначе не понятно на следующих картинках как выражение может быть одновременно и желтое и фиолетовое.
nin-jin Автор
В классической логике это обходится так: A=B — это не утверждение, а формула с двумя свободными переменными. Утверждением оно станет, когда вы подставите вместо этих переменных какие-либо утверждения. И только тогда в классической логике можно спрашивать правдиво оно или ложно. А без подстановки — нельзя.
technic93
Ну а в четырехзначной как?
nin-jin Автор
В статье же написано..
technic93
Вот есть утверждение "This is True" для него мы показали что оно "Can be True" и "Can be False" и поэтому жёлтое. А про "A=B" я ничего не могу показать, каким образом мы его смогли раскрасить?
nin-jin Автор
Вот поэтому и жёлтое. Недостаточно данных.
technic93
А как мы узнаем достаточно данных или нет. Может мы просто не додумали, поэтому оставили какое-то утверждение желтым, хотя на самом деле оно другого цвета. Что делать?
nin-jin Автор
Так же как с недоказанными теоремами — истинность их не известна, пока не "додумали".
AnthonyMikh
То есть я правильно понимаю, что в четырёхзначной логике категория, к которой принадлежит утверждение, зависит от степени развития математического знания?
nin-jin Автор
В любой логике так.
technic93
Кстати firefox ругается на ваши cлайды :(
The loading of “https://raw.githubusercontent.com/nin-jin/slides/master/absurd/fire.jpg” in a frame is denied by “X-Frame-Options“ directive set to “deny“.
nin-jin Автор
Спасибо, поправил.
farafonoff
Доказательство кантора — конструктивное, оно «строит» число неравное другим числам диапазона. Ваша упрощенная формула по сути — тавтология, она постулирует что мы пронумеровали все вещественные числа, и из этого выводит что непронумерованных не осталось.
nin-jin Автор
Это не так ибо там пропущен шаг конструирования биекции.
С тем же успехом можно строить и такое число: идём по ряду натуральных чисел и на каждом шаге прибавляем единичку, а не 0 или 1/2^n как в диагональном методе. Предельный переход и мы получили натуральное число, которое не равно никакому натуральному числу. Это типичный парадокс актуальной бесконечности.
mayorovp
Вот начиная с этого шага (который делается от противного) оно и является конструктивным.
Предположили, что биекция существует — и конструктивно построили контрпример.
Can be false, cannot be true. Утверждение "R — счётное множество" ложно даже в вашей четверичной логике.
nin-jin Автор
Типа если согрешил, а потом покаялся, то стал безгрешным?
mayorovp
Приравнивать рассуждение "от противного" к "согрешил" можно только в рамках интуиционисткой логики. Но приведённая вами логика на таких рассуждениях чуть ли не основана.
0xd34df00d
Спасибо за расшифровку видео, вы сэкономили мне время.
Нет. 2 + 2 = 4 тоже может быть ложным. Рассмотрим интерпретацию, где a + b определяется как a, например, или как 2, для любых a и b. У вас нет никакого способа отличить высказывания 2 + 2 = 4 от A = B внутри логики, не рассматривая интерпретации. По аналогичным причинам 2 + 2 = 3 может быть истинным — подбор интерпретации, где это так, предлагается читателю в качестве упражнения.
2 = + — некорректное синтаксически высказывание. Его отсекает formation rule.
Вам не нужно четыре значения, чтобы что-то там классифицировать.
Конструктивисты смотрят на этот метод как на… плохо смотрят, короче.
Далеко не во всякой теории вы можете записать такую ссылку на себя. Это не очень тривиально.
Не в любой, а только в достаточно мощной, чтобы выразить арифметику Пеано (иначе сослаться на это утверждение не получится).
Непонятно, как вы сделали такой вывод.
Если честно, получилось у вас плохо, и это совсем не про теорему о неполноте.
В математику лет 150 назад начали и лет 100 назад закончили завозить понимание, что для рассуждений нужна формальная система. И оказывается, что, например, в ZF вы такое высказывание просто тупо записать не сможете. Оно не парадоксальнее упомянутых вами ранее 2 = +.
Вы не поняли доказательство Кантора. Более того, вы не понимаете, что такое доказательство от противного.
К счастью, конкретно это рассуждение мы не так давно обсуждали в другом треде, так что я его просто процитирую
defuz
Спасибо за ваш героизм, я до конца не осилил!
Интуиционисты одобрительно поддакивают конструктивистам.Здесь на слезах Кантора можно будет построить небольшую ГЭС. Но там цирк начинается еще на словах «берём случайное вещественное число».
nin-jin Автор
Бессмысленную риторику, я, конечно, пропущу.
Вы путаете причину и следствие. formation rule такой, какой он есть, именно для того, чтобы отсекать абсурд. Но не весь абсурд возможно отсечь синтаксически. О чём и свидетельствуют многочисленные парадоксы.
О том и речь. Математики разбились на школы и смотря на выводы соседей крутят у виска.
Бессмыслица не даёт никакой информации о внешних, по отношению к ней, объектах. Вы считаете иначе?
Вы очень любите приводить везде код на никому не понятных языках. Вы хоть иногда задумываетесь о смысле сего действа?
AnthonyMikh
Надо читать как "я почти ничего не понял, так что буду
доёдокапываться до собеседника по тому, что понял".Именно, поэтому в формальных языках, помимо formulation rules, обычно есть derivation rules.
Если некоторое утверждение бессмысленно, то как вы вообще можете разделить объекты на внешние и не внешние по отношению к нему?
О, а вот это — прям каноничный случай парадокса Блаба, прям можно поместить в рамочку и вешать на стенку.
Я надеюсь, вы осознаёте, что если вы чего-то не знаете, то это не значит, что этого не могут знать другие?
nin-jin Автор
Для бессмысленного выражения все объекты внешние.
???????????????????????????????????
defuz
Никто с вами не будет обсуждать формальные исчисления на японском языке или на языке разноцветных прямоугольников.
AnthonyMikh
??????????????????????????????????????????????????????????????????
nin-jin Автор
Это общая проблема, ибо конструктивное общение в таком случае становится невозможным.
mayorovp
Верну-ка я вам ваш старый аргумент.
С таким уровнем аргументации вам сюда: https://fallacy.hyoo.ru/#selected=shape~complexity/filter=selected
nin-jin Автор
В данном случае вы применяете эту технику: https://fallacy.hyoo.ru/#selected=dummy/filter=selected
Жалоба на то, что собеседник намеренно использует непонятный синтаксис, не является аргументом. Вы подменили неопределённость ложью. Что лишний раз показывает непродуктивность бинарного мышления, свойственного классической логике.
mayorovp
Чем жалоба на непонятный синтаксис отличается от жалобы на непонятный набор слов?
franzose
Хабр всё еще торт? :)
0xd34df00d
Он не отсекает асбурд. В матлогике вообще нет понятия абсурда в том смысле, о котором вы говорите. «2 + 2 = 3» — не абсурд. «Если Вася сегодня ел снег, то снег белый» — не абсурд. И даже не парадокс.
В том и дело, что не крутят. Классическая логика хороша в одних контекстах, интуиционистская — в других.
Я не могу формально интерпретировать эту фразу (в частности, потому, что в матлоге нет понятия бессмысслицы). Но если я получил ложь из каких-то предпосылок, то, значит, эти предпосылки были неверны.
Во-первых, агда — стандартный инструмент в этой области, во-вторых, здесь (сугубо ИМХО, конечно) нет ничего, что не было бы понятно человеку с опытом хотя бы хаскеля, в-третьих, это всё даже неважно — достаточно того, что есть код, он тайпчекается, и дальше достаточно знаний о том, что агда из тех языков, где используется конструктивная логика. Но если вы не знаете, что в конструктивной логике нет аксиомы исключённого третьего, которая эквивалентна снятию двойного отрицания, через которое и работает доказательство от противного, то, конечно, прошу прощенья за резкость, но такие статьи вам писать ещё рано.
defuz
Автор, если вам так не нравятся выводы Кантора, наличие актуальных бесконечностей в математике, и прочая запрещенная магия, рекомендую вам ознакомиться с наработками конструктивистов и интуиционистов. Они уже лет 100 как работают в том направлении, которое вы крайне не формально (от слова формализация) начали в этой статье.
Sayonji
Ужас какой, мой iq уменьшился на 5 от просмотра этой статьи.
Alexufo
Давайте рассуждать логически, что вы хотели сказать.
1) вы ощутили себя глупым и это знание вычло всего лишь 5 единиц из вашего IQ. Завидую вашей психологической защите.
2) Вы ощутили себя глупым и ваш iq упал до 5. Вы почти присмерти, хлеб сложно будет купить, слова лучше записать на бумажке для кассира. Не завидую вашей психологической защите.
3) Вы издеваетесь и смеясь автору в лицо, сообщаете, что отупели из-за чтения. То есть автор виноват, что вы отпупели.
Хм… пока расписал ваш комментарий понял, что раз вы неточно сформулировали мысль, то есть не предположили вариативности трактовки, думаю вы про пункт 2. Заходите ко мне, попьем чайку
Cerberuser
Не могу не спросить, какая буква здесь лишняя? А то читается немного двояко...
Alexufo
Да вроде все понятно. Прочитал текст, стало плохо от контента, познал глупость вместо знания.
Ru6aKa
Знал я одного человека, так вот он тоже придумывал свою четырёхзначную логику, но назвал её биквадратной. И знаете что? Спился.
AlexandrNikolaichev
Крашу статью в фиолетовый.
А если серьёзно, рекомендую «Введение в метаматематику» Стивена Клини. Большинство вопросов отпадут.
0xd34df00d
У него довольно тяжёлый, на мой взгляд, язык (мне с некоторым опытом чтения книг и статей на английском было тяжко). Отечественные Верещагин и Шень, «Лекции по математической логике и теории алгоритмов», лежащие в открытом доступе на mccme.ru, имхо вполне неплохи.
mayorovp
У вас логическая ошибка. Если оно ложное — то из её отрицания следует его не-ложность, т.е. один из трёх вариантов — правдивость, абсурд, неопределенность.
Пока что эта ошибка ни на что не повлияла, но она показывает качество "проработки" логики.
Предлагаю вместо этого рассмотреть утверждение "это утверждение либо ложно, либо абсурдно".
Если оно правдиво — получаем парадокс. Если оно ложно — получаем парадокс. Вроде бы оно должно быть абсурдным… но в таком случае оно должно быть хотя бы правдивым.
Нет, мы его не доказали, ведь кроме ложности для доказательства следует отвергнуть также вариант "абсурд".
Всё это замечательно, вот только эти рассуждения не имеют никакого отношения к непротиворечивости системы аксиом вашей логики (которые вы даже не попытались привести).
nin-jin Автор
Это не ошибка, а опускание несущественных деталей для простоты восприятия. Неопределённости тут нет, ибо не-ложность исключает и неопределённость. А абсурд — это нулевая гипотеза, которую нет смысла рассматривать отдельно, ибо он и так получается при отвержении всех остальных вариантов. Если выражение абсурдно, то на этом рассуждения заканчиваются и гипотеза отбрасывается.
Эта дихотомия разбирается в разделе про Гёделя.
Вы невнимательно прочитали. Попробуйте ещё раз. В теореме Гёделя непротиворечивость задаётся как исходная посылка.
Ну а логика не моя. В конце статьи есть ссылка на её описание с аксиомами, правилами вывода, таблицами истинности и вот этим всем.
mayorovp
В таких низкоуровневых вещах не бывает несущественных деталей.
С какого перепугу?
С какого перепугу?
Но я критикую ваш пост, а не ту ссылку с аксиомами, правилами вывода и прочим.
mayorovp
До кучи:
Вы сейчас что, в принципе запретили приходить к противоречию в рассуждениях от противного? Я ведь точно так же могу поступить с каждым вашим утверждением из этого поста!
Например, вот с этим:
Но ведь в рамках исходной гипотезы утверждение правдивое, значит нельзя рассматривать случай когда оно ложное. Получается, никакого противоречия нет и утверждение из парадокса лжеца — не абсурдное, как попытались показать вы, а правдивое!
nin-jin Автор
Попробуйте прочитать статью не по диагонали, а вдумчиво, тогда претензий будет куда меньше.
mayorovp
Попробуйте прочитать учебник по теории множеств не по диагонали, а вдумчиво, тогда претензий будет куда меньше.
technic93
Предоставьте ваш алгоритм и генератор случайных вещественных чисел, а мы найдём числа которые он не покрывает.
nin-jin Автор
В теории вероятностей нет никаких генераторов случайных чисел. Есть только выборка из множества, с заданными отношениями вероятностей между элементами. Это не конструктивная математика.
technic93
тогда я могу сказать что я буду брать случайное доказательство до тех пор пока оно не окажется правильным. Таким образом я докажу любую теорему. Профит.
Апд. В предыдущем комментарии я процитировал ваше высказывание. оно явно конструктивное.
Как так получается конструктивное доказательство не конструктивно
Апд2. Ну как бы если строить теорию вероятности по честному, через меру и сигма алгебры, то там придется решать задачу с несчётными множествами по новой. Так что никуда от них не уйдёшь. Собственно поэтому нужно сначала решить вопрос с множествами а потому уже браться за теорию вероятности. Иначе теория вероятности превращается в "вероятность встретить динзовара 50%".
Graphite
Предположим, что я не обращаю внимания на все остальные проблемы в посте — о них уже достаточно написали.
Когда вы говорите "берём случайное вещественное число" вы неявно вводите утверждение вида "существует способ выбрать случайное вещественное число, такой, что любое вещественное число может быть выбрано с ненулевой вероятностью".
Чтобы его использовать надо проверить его на истинность. Где эта проверка? Только, пожалуйста, без волшебного способа доказать что угодно.
nin-jin Автор
https://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D0%BF%D1%80%D0%B5%D1%80%D1%8B%D0%B2%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D0%B2%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5
Graphite
Непрерывное распределение существует конечно же. А способ-то какой и почему он существует?
nin-jin Автор
А какой ответ вас мог бы удовлетворить? Теорвер принципиально не конструктивен. В нём нет никакого алгоритма генерации случайного числа, ибо тогда оно перестало бы быть случайным.
Graphite
Удобно. Вы вводите утверждение в ваше доказательство которое не надо доказывать, потому что оно неконструктивно.
Проблема в том, что данное утверждение эквивалентно утверждению "множество действительных чисел счётно", так что ничего удивительного в том, что вы к такому выводу приходите.
Я понял все что хотел.
nin-jin Автор
На практике от теорвера бесконечно больше пользы, чем от несчётных множеств. Так что из двух аксиом, стоит выбирать более продуктивную.
koldyr
То что аксиоматическая теория вероятностей построена на теории меры вас видимо не беспокоит. Как и интеграл Лебега.
nin-jin Автор
В математике много теорий которые можно вывести друг из друга. Выбор какая теория будет базовой, а какая производной, достаточно произвольный. Хорошие кандидаты на базовость — достаточно простые, интуитивно верные и содержащие не выводимые из других теорий части.
Но всё, на самом деле, ещё хитрее: из частей одной теории могут выводиться части другой, из которых уже новые части первой. Главное, чтобы в выводах не было циклов.
koldyr
Раз без циклов, то, в данном случае, предъявите теорию вероятностей без теории меры.
koldyr
Осень.
AnthonyMikh
Обычно обострение по весне, разве нет?
user_man
Предложенное «доказательство» счётности множества действительных чисел не полное.
Возьмём любое натуральное число, например единицу (для простоты), добавим к нему одну десятую, получим действительное число, а помимо того — алгоритм задания взаимного соответствия, который можно применить к любому натуральному числу и в результате получить соответствующее каждому натуральному действительное число. Подчеркну — каждому натуральному, не смотря на бесконечность их количества.
Теперь берём число, например, 0.5. И видим, что если мы применили выше показанный алгоритм, то для действительного числа 0.5 не останется натуральных чисел, не вошедших в отношение с действительными.
Более полный вариант доказательства счётности мог бы выглядеть так — сначала отменяем общепринятую в неаксиоматической теории множеств аксиому (которая есть просто привычное всем определение). Это определение сообщает нам, что счётным можно признать множество, каждому элементу которого можно сопоставить натуральное число. Если мы заменим эту аксиому на следующую — счётным можно признать множество, каждому элементу которого можно сопоставить уникальный идентификатор, то сразу появляется пространство для манёвра в случае с числом 0.5 и сопоставлением натуральных чисел с их суммой с одной десятой. Например, можно задать идентификатор в виде натурального числа, соответствующего интервалу в одну десятую, и ещё пары натуральных чисел a и b, соответствующих соотношению a/b, дающему в результате целевое значение для действительного числа, которому мы сопоставляем идентификатор.
Точно так же можно разрешить все парадоксы в вашей статье — просто меняем ваши аксиомы или вводим новые. Например, брадобрей может удовлетворять всем условиям, если мы удалим аксиому, запрещающую множествам бреющихся и бреемых пересекаться. Тогда Санта станет живым.
Ну и более общий вариант — ваша сколько угодно многомерная логика всё же опирается на логический вывод, который остаётся всё тем же — задаём аксиомы, строим правила вывода и далее получаем следствия. И для этого набора существуют вполне строгие правила — если вы получили абсурд (или противоречие), то значит вы задали некорректный набор аксиом. Или неполный (в явном виде у вас вообще аксиомы не обозначаются, что сводит их количество к нулю). Как только задаите корректный набор аксиом и правил вывода, так сразу исчезнут все парадоксы и абсурды.
Кстати, абсурд, это отсутствие смысла. А смысл задаётся исходными аксиомами. Если смысла нет — вы некорректно задали набор аксиом, потому что он позволяет выводить бессмыслицу. То есть нет разницы между противоречием и абсурдом, они оба есть следствие некорректности (неполноты) набора аксиом.
vitaly_zyr
Мне кажется, что вы неправильно называете описываемую вами логику «классической». Правильное название — формальная логика. Диалектическая логика также классическая, но она с этой имеет лишь общий момент, но и только.
А еще вот никогда не понимал «парадокс Брадобрея»: сначала принимается аксиома, что существует 2 не пересекающихся множества. Затем вводится новая аксиома, что множества пересекаются. А вывод об абсурдности делается на основании несоответствия первого набора аксиом новой аксиоме. Получается, что первый набор аксиом, который не полностью описывает систему, оценивают против набора, который полностью ее описывает и делается вывод, не о неполноценности «неполного набора», а об абсурдности всей системы. Странно…
nin-jin Автор
https://ru.m.wikipedia.org/wiki/%D0%9A%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0#:~:text=%D0%9A%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F%20%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0%20%E2%80%94%20%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D0%BD%2C%20%D0%B8%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D1%83%D0%B5%D0%BC%D1%8B%D0%B9%20%D0%B2,%D1%82%D0%BE%D0%BC%20%D1%87%D0%B8%D1%81%D0%BB%D0%B5%20%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%20%D0%B8%D1%81%D0%BA%D0%BB%D1%8E%D1%87%D0%B5%D0%BD%D0%B8%D1%8F%20%D1%82%D1%80%D0%B5%D1%82%D1%8C%D0%B5%D0%B3%D0%BE.
Не вводится там аксиом о пересечении, вводится описание нового объекта, который в данных условиях существовать не может.
andreyverbin
Не «бесконечно мала», а «точно равна нулю» и поэтому даже если у вас бесконечно число попыток, то множиться оно будет на 0. И все последующие рассуждения про равенство бесконечностей уже не имеют смысла. Чтобы ваш аргумент сработал, вам нужно определить свою теорию вероятности. Но с этим будут некоторые проблемы.
Но давайте попробуем порассуждать, что будет если «бесконечно мала вероятность» все таки есть. Возьмем интервал [0, 1] и допустим, что вероятность попасть бесконечно тонкой указкой в число 0.5 (и любое другое) равно dk. dk это такое специально число, с особыми свойствами — «бесконечно малая величина». Основное свойство — любая конечная сумма таких величин равна самой величине, то есть dk + dk = dk
В нашем примере интеграл от 0 до 1 по dk равен 1, это требование тер вера. Теперь возьмем интервал [0, 2] и допустим, что вероятность попасть бесконечно тонкой указкой в число 0.5 (и любое другое) равно dq. Интеграл от 0 до 2 по dq будет равен 1. Отсюда можно сделать вывод, что 2*dq = dk, то есть dq + dq = dk, но выше мы договорились, что dq + dq = dq. Беда. Если же сказать, что dq = dk, то получится, что вероятность попасть в 0.5 на интервале [0,1] такая же как и на интервале [0, 2], то же беда.
Понятие «бесконечно малых» было популярно в 19 веке, но сейчас не используется в стандартной математике, потому что его было сложно определить точно. Есть нестандартный анализ, в котором «бесконечно малая величина» есть. Удобно сказать, что dx это такое специальное число, «бесконечно малое число», за это топил Лейбниц. Кроме проблемы, описанной выше возникает намного большая. Если dx добавить в поле вещественных или комплексных чисел, то появляются делители нуля, а поле перестает быть полем. Это значит, что уравнения уже просто так не решаются, существенная часть результатов линейной алгебры идет лесом и много чего еще.
0xd34df00d
В нестандартном анализе оно всё вполне добавляется, и поле остаётся полем, все дела. Просто бесконечно малых (и бесконечно больших) оказывается бесконечно много, и они все разные, и с ними работают те же формулы и определения операций, что и для обычных вещественных чисел (в этом и весь смысл нестандартного анализа, и так получается по построению по теореме Левенгейма-Сколема о повышении мощности).
andreyverbin
Было бы интересно об этом почитать, можно ссылки?
Я тут подумал и кажется я выше вообще фигню написал про dq + dq = dq. Но это не так и важно, потому что вероятность ткнуть в R и найти конкретное число все равно 0. Автору нужно ввести свой тер. вер. и уже после этого говорить про инъекцию R в N.
0xd34df00d
Сошлюсь на вышеупомянутых Верещагина и Шеня. Там в конце есть целая глава про нестандартный анализ, где можно по желанию идти по отсылкам назад к матлогическим обоснованиям соответствующих теорем.
nin-jin Автор
Бесконечно малое — это вообще функция. Пределом её будет ноль, но это не имеет значения. Важно, что для любой дельты в окрестности заданного числа вероятность попасть в неё не нулевая.
Тут есть ещё и такое элегантное доказательство:
Это первый курс матана..
technic93
Вероятность получить число 1 на каждом шаге х. Вероятность не получить его за n шагов (1-х)^n. Как раскрыть эту неопределенность?
nin-jin Автор
В чём неопределённость-то?
technic93
x=0, n=infinity
nin-jin Автор
Тут нет неопределённости, предел равен нулю.
technic93
на каком основание вы разрешаете очерёдность взятия пределов?
если предположить линейную связь между 1/x и n то получится как известно e
можно предположить что 1/x растёт быстрее тогда получится 1, можно предположить обратное и получить 0. Чтобы это решить надо понять связь между множеством числа шагов, т.е. натуральных чисел и множеством вещественных. Т.е. от главного вопроса у вас уйти не получится, как я писал уже выше
nin-jin Автор
2,3. Нет никакой связи между ними. Иначе они бы выражались одной переменной.
technic93
Хорошо теперь рассмотрим вероятность сгенерировать число A на шаге n+1, Это x * (1 — x) ^ n = 0 для любого n.
nin-jin Автор
Вероятность сгенерировать конкретное число за любое конечное число шагов бесконечно мала, да.
technic93
Ой. Это был не тот контр пример, лучше рассмотреть вероятность получить на каком-то шаге любое натуральное число на от 1 до n, т.е. x * n. Теперь чтобы найти вероятность получить любое натурально число, надо взять n = бесконечность. Поскольку это должно быть < 1 вам придётся наверно сначала брать предел по икс. Тогда все же как понять очерёдность пределов...
nin-jin Автор
Не очень понял суть, но чего вы пытаетесь добиться? Опровергнуть теорию вероятностей?
technic93
Да я показываю что ваша интерпретация теории вероятности не верна.
nin-jin Автор
Даже если вам это удастся, вы же понимаете, что из этого не будет следовать, что существуют несчётные множества?
koldyr
Существование несчетного множества это другая теорема. О том, что множество всех подмножеств несоизмеримо с исходным. Правда классическое доказательство — от противного.
nin-jin Автор
Там тоже используется Санта, причём в чистом виде, безо всяких диагональных методов.
ildarz
Санта — выдуманная вами сущность. Вы ее сами вводите, сами показываете, что получается ерунда, но вывод почему-то делаете не о том, что это проблема в ваших рассуждениях, а о том, что это с теоремами (которые в оригинале никакого Санту не вводят) что-то не так.
nin-jin Автор
Вы, прежде, чем бросаться обвинениями, ознакомьтесь сперва с предметом: https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9A%D0%B0%D0%BD%D1%82%D0%BE%D1%80%D0%B0
Вообще, Савватеев тут говорит замечательную мысль: "если вы не готовы поверить в существование Санты, то вы не математик".
ildarz
Ctrl+F, "Санта", 0 результатов. Сформулируйте строго, что вы пытаетесь доказать или оспорить, тогда и посмотрим, кого надо знакомить с предметом.
0xd34df00d
Савватеев — немножко поехавший фрик, к которому среднее отношение среди других математиков типа «ну пусть играется в своей песочнице».
Но больше всего меня, конечно, позабавил его тезис году в 2018-м, что компьютеры точно не могут проверять корректность доказательства теорем. С теорией игр, про которую он обычно рассказывает, мне спорить сложно, у меня её всего семестр был.
technic93
Ну в видео оно немного путано объясняется. Проще рассуждать так. Рассмотрим произвольную функцию
f: A -> 2^A.Определим
BкакТеперь давайте узнаем существует ли
y ? Aтакой чтоf(y) = B. Тут начнём действовать от противного — пусть существует.Если
y ? Bто по условию (1) имеемy ? f(y)— противоречие.Если
y ? Bто по условию (1) имеемnot (y ? f(y))=>y ? f(y)— противоречие.Следовательно не существует такого
y, который был бы образомBдля функцииf.Таким образом для любой функции
f, существует такойB, который не принадлежит отображениюf. Следовательно биекция невозможна.technic93
Т.е. Санта это "множество всех подмножеств"?
nin-jin Автор
Санта — это множество B из Википедии.
technic93
Так ответьте на последний вопрос. Всё таки x * n чем равно, и как это показать? Условно говоря если 1/x "больше" n тогда вероятность не найти данное число равна одному. И наоборот.
andreyverbin
Вы говорили о бесконечно малой вероятности, а это число, его и обсуждали. Бесконечно малые как функции или ряды мне известны, но вы же не имели в виду, что вероятность выбрать вещественное число равна какому-то ряду?
В множестве R содержится счётное количество дельта окрестностей и несчетное количество чисел. Занумеровать окрестности — пожалуйста, занумеровать сами числа — не выйдет.
Постулат #1 верен только если вероятность равна 0, иначе интеграл по бесконечности чисел разойдётся, а должен быть 1. Хотите чтобы сходился к 1 — вводите бесконечно малые числа и разгребайте последствия.
0xd34df00d
Только на этом первом курсе ещё рассказывается, что бесконечно малые — последовательности, а не числа. Это объекты разных типов, если хотите, и в обычном множестве вещественных чисел никаких бесконечно малых (и бесконечно больших) нет.
defuz
Автор, предлагаю вам решить следующую головоломку:
Допустим, ваша математика не противоречива, и нам дарован свыше волшебный генератор вещественных чисел, которым вы так лихо оперируете (сама принципиальная осуществимость которого уже крайне сомнительна).
Решите задачу #1: Какова вероятность на произвольной итерации получить положительное, либо отрицательное число?
Решите задачу #2: Какова вероятность на произвольной итерации получить число больше, либо меньше одного миллиона? (подсказка: воспользуйтесь выводом из первой задачи, значение один миллион не имеет значения)
Решите задачу #3: Какова вероятность на произвольной итерации получить число в диапазоне от нуля до миллиона, если пользоваться результатами первых двух задач?
Решите задачу #4: Какое количество попыток необходимо совершить, чтобы получить число в диапазоне от нуля до миллиона с вероятностью 50%, исходя из результата третей задачи? (подсказка: значение 50% не влияет на ответ, но у вас может быть другое мнение)
Мне интересен ваш ход мыслей.
mikhanoid
Текст, конечно, чухня, потому что nin-jin не владеет матчастью. Но кажется, что чухня не полная, не бесполезная и не безынтересная. Хотелось бы, чтобы nin-jin не забивал на эти рассуждения, а развил бы их, прежде всего, корректно соотнеся их с существующим положением дел в современной логике.
ildarz
Теорема Гёделя не о том, что существуют недоказуемые утверждения в сферическом вакууме, а о том, что существуют утверждения, недоказуемые в заданном наборе аксиом. Да, они будут истинными, но ваше утверждение о том, что мы "доказали" утверждение по Гёделю и тем самым якобы получили противоречие — неверно, потому что теорема Гёделя не входит в вышеуказанный набор аксиом.
Не постулировали, а предположили.
nin-jin Автор
В произвольном достаточно сильном.
Не смог распарсить эту мысль. Я ничего "по Гёделю" не доказывал.
Как-то очень уж безусловно предположили. Это и называется постулат.
ildarz
Но, тем не менее, заранее заданном и фиксированном. Суть теоремы — для любого фиксированного набора аксиом, обладающего определеными свойствами, есть утверждения, которые не могут быть доказаны или опровергнуты в рамках именно этого набора аксиом (а не любого "произвольного достаточно сильного"). Если верность этих утверждений показана каким-то другим способом — никакого противоречия не возникает.
Бывает.
Это ВЫ "безусловно предположили". А Кантор тут ничего не предполагает — он просто приводит алгоритм, который строит вещественное число, не входящее в "пересчитанные". Поэтому вы "опровергли" сами себя, но не Кантора.
saaivs
Буду искренне признателен, если кто-то мне укажет на математическую ошибку в рассуждениях, которые возникли по другому вопросу, но там тоже возникла задача соответствия между подмножеством вещественных чисел и счётным множеством.
Определение. Вещественное ? число есть бесконечная десятичная дробь, то есть выражение вида:
±a(0),a(1)a(2)...a(n)… где a(0)? ?, т a(i)?{0,1,2,3,4,5,6,7,8,9} для ? i? ? ( Отсюда ru.wikipedia.org/wiki/Конструктивные_способы_определения_вещественного_числа#Теория_бесконечных_десятичных_дробей )
Факты:
(1) Все точки отрезка [0, 1] имеют мощность континуума c ( https://ru.wikipedia.org/wiki/Континуум_(теория_множеств) )
(2) Счётны множества всех конечных слов над счётным алфавитом и множество всех слов над конечным алфавитом. ( ru.wikipedia.org/wiki/Счётное_множество )
(3) Счётными являются объекты, получающиеся в результате рекурсивных процедур.
Получается, что, с одной стороны на интервале [0,1] все вещественные числа мы можем записать в десятичном виде по определению, а с другой стороны, согласно определению выше — это множество будет иметь континуальную мощность.
Но, множество таких записей в силу (2) счётно, а значит на интервале [0,1] существуют такие числа из ?, которые не попадают в наше множество, а значит их невозможно записать в виде бесконечной десятичной дроби. И не по причине того, что там бесконечность. Построить процесс перечисления(вычисления) всех возможных записей десятичных дробей вплоть до бесконечности как раз никакого труда не составляет(см. ниже). А получается в принципе нельзя, т.к. они не представимы в таком виде, поскольку дополнение с/?(0) ? ?
Получается, что не любое вещественное ? число представимо в виде бесконечной десятичной дроби?
Поскольку все десятичные числа на интервале [0,1] имеют вид 0,a(1)a(2)...a(n)…, при том, что числа {0,05; 0,050; 0,0..05(0) } — неотличимы, то нам достаточно рассмотреть множество S всех строк из десятичного алфавита без терминального 0(в том числе бесконечной длины), которое будет содержать все возможные записи мантисс действительных чисел в силу определения.
S = {
0.1 -> '1', 0.2 -> '2', ..., 0.9 -> '9',
0.01 -> '01', ..., 0.99 -> '99',
0.001 ->'001', ..., 0.999 ->'999',
…
}
Для каждой длины строки n несложно рекурсивно перебрать все возможные комбинации:
n=1: 0...9
n=2: 01,02, ...,99
n=3: 001, ..., 999
…
n: (0 n раз)1… (9 n раз)
? n? ?
С точки зрения заполнения интервала [0,1] процесс построения чем-то похож на заполнение ru.wikipedia.org/wiki/Канторово_множество, но только наоборот(не вырезаем, а достраиваем относительно десятой части каждого полученного отезка).
При n>? получим бесконечное множество S строк различной длины, которое перечисляет все возможные комбинации цифр десятичного алфавита по построению.
Такое множество задаётся рекурсивным способом, а значит в силу (3) оно является счётным.
На множестве S естественным образом (по длине строки и десятичным знакам) задаётся отношение частичного порядка и взаимно однозначное соотношение между ? и S можно задать аналитически, а не только рекурсивно.
Если,
( a ) len(s) — функция, возвращающая длину строки;
( b ) pad(n, l) — функция, преобразующая число n в строку и добавляющая слева число нулей так, чтоб общая длина строки стала равна l;
( c ) num(s) — убираем з строки лидирующие нули и строку преобразуем в целое число;
(d) ?x? — «антье», целая часть числа, округленная в меньшую сторону.
то пусть: ?s?S, ?n??, l = len(s), k = num(s)
F(s) = 10^(l-1) — ?k/10? + k — 1 (для строки вычисляем её номер)
G(n) = pad(x,l), где x — корень уравнения: x — ?x/10? = n — 10^(l-1) + 1 (по номеру вычисляем строку, но тут потребуется рекурсия глубины l для вычисления решения уравнения)
Примечание: Ещё раз, чтоб не было безсмысленных споров — это рассуждение не доказательство счётности континуума, а рассмотрение случайно возникшей гипотезы, что не все вещественные числа представимы в десятичной форме, даже бесконечной длины, из-за того, что не понимаю, где тут ошибка :) Поможете её опровергнуть?
koldyr
Множество бесконечных строк над конечным алфавитом несчетно.
Про построение — фокус в хвостах рядов. Множество голов рядов — счётно, а вот хвостов — нет.
saaivs
Спасибо, за ответ!
А можете пояснить, что вы имеете в виду под «голов» и «хвостов», и какой «фокус»?
Вкратце:
1) Я же рассматриваю только интервал [0,1], который есть континуум.
2) Затем, согласно определению десятичной записи числа определяю множество строк, которые фактически соответсвуют всем возможным формам записи таких чисел, в том числе и бесконечной длины.
3) Показываю биекцию между этим множеством и множеством натуральных чисел.
4) Констатирую, что дополнение счётного множества до континуума непусто, из чего делаю вывод, что «все возможные формы записи десятичного числа на интервале [0,1]» не содержат некоторые вещественные числа.
Какой конкретно шаг, или какое утверждение, на ваш взгляд ошибочно?
P.S.
Это да. Но построение множества «всех возможных форм записи десятичного числа на интервале [0,1]» (S) легко описывается как рекурсией, последовательно перебирая все возможные вараинты для каждой длины строки, так и аналитически между таким множествои и натуральными числами задаётся биекция при помощи вычислимых процедур, что однозначно говорит о его счётности. Либо тут S строится некорректо и не содержит некоторые десятичные числа, описывая лишь некоторое счётное подмножество вещественных числел таким построением. Но тогда какие числа(какого вида) сюда не входят? Вот этого я понять не могу…
koldyr
Вещественное число это не бесконечная десятичная дробь, а предел последовательности. Видимо ошибка здесь.
saaivs
Так как раз к этому у меня вопросов и нет. С вещественными числами и их мощностью всё понятно. Мне показался любопытным вопрос, а все ли вещественные числа можно записать в десятичной форме в принципе. Вначале думал что, нет — там же бесконечность. Но натуральные числа обладают тем же самым свойством — для записи бесконечно большого натурального числа тоже нужно бесконечное число цифр. А любое вещественное число, цифры в дестятичной записи которых мы может вычислять с бесконечной точностью (например Пи) тоже является его аналогом(как раз как предел последовательности). Только на множестве натуральных чисел такое число видимо одно — предел последовательности натуральных чисел, а среди вещественных таких бесконечное количество (как раз то самое множество строк бесконечной длины над конечным множеством ) континуальной мощности.
Но вся незадача, возникла от того, что сама по себе процедура представления «всех форм представления вещественных чисел в десятичной форме на интервале [0,1]» формирует счётное множество, из чего следует либо: (1) либо такое построение описывает представление не всех вещественных чисел — но, тогда какие не описывает?; (2) либо существуют десятичные числа, принципиально не представимые в десятичном виде — тогда что это вообще такое?
defuz
Вы путаетесь между понятиями актуальной и потенциальной бесконечности.
Для любого, сколь угодно большого натурального числа, необходимо счетное и конечное количество цифр для его записи.
Для любого иррацинального числа, сколь угодно большого количества цифр будет недостаточно, чтобы записать его.
Ключевое слово – «конечных». Запись числа Пи не является конечной в десятичной форме.
Ключево слово – «результат». То есть только при условии остановки вычисления в том смысле что каждый элемент множества потенциально осуществим – вычисляется за конечное число итераций.
«Можем записать» – это очень сильное утверждение, поскольку бесконечное количество чисел на этом интервале будет иметь бесконечное представление, а бесконечное количество цифр мы записать не можем в том смысле, на который вы опираетесь.
Нет, потому что это множество будет состоять в том числе из актуально бесконечных, а не только конечных записей.
Зависит от того, как вы определяете «любое вещественное число» и «представимость». В классическом понимании, вещественное число можно представить в виде потенциально бесконечной десятичной дроби в том смысле, что вы можете сконструировать алгоритм, позволяющий узнать i-ую цифру записи, для любого конечного значения i. Но это не значит, что записать полностью число пи – потенциально осуществимая операция, поскольку требует актуально большого количества цифр. В таком смысле можно говорить, что иррациональные числе не представимы в виде десятичной дроби.
Здесь ошибка состоит в том, что каждому иррациональному числу будет соответствовать мантисса актуально бесконечной длины, а значит и «натуральное число бесконечной длины», но таких натуральных чисел просто не существует.
defuz
Тут скорее имеет смысл поднять вопрос, будет ли содержать такое множество слова бесконечного размера. Содержит ли множество натуральных чисел значения бесконечной длины? В смысле потенциальной бесконечности – да, в смысле актуальной бесконечности – нет.
saaivs
Не путаю) Я не знал от такой классификации бесконечностей. Спасибо большое за ссылки.
В принципе, это же рассуждение применимо и к натуральным числам, поскольку некоторое натуральное тоже число можно представить в виде потенциально бесконечной десятичной записи цифр. Ограничений на длину такой записи нет.
Собственно, это как раз то самое противоречие, к которому я и пришёл. Натуральное число бесконечной длины — это же бесконечность, как предел ряда натуральных чисел, а он сам по себе не является натуральным числом. Я рассматриваю не совсем строки «бескончной дины», а математический объект, который по построению не имеет ограничений сверху на длину своего представления. В том же самом смысле, в котором «сверху» не ограничено множество натуральных чисел.
Как хорошо заметил 0xd34df00d
По сути, ларчик просто открывался: Я строил множество заведомо вычислимых чисел. А порядок на множестве вычислимых действительных чисел изоморфен порядку на множестве рациональных чисел.
Соответственно множество всех вычислимых чисел является счётным множеством, а множество вот всех невычислимых чисел — несчётным.
mayorovp
Но любая бесконечная последовательность цифр натуральным числом от этого не станет (…11111 вам как контрпример).
saaivs
А это и не утвержалось. Дело не столько в длине представления, а сколько в вычислимости таких чисел. Вот тут подробнее.
0xd34df00d
Зависит от аксиоматизации.
mayorovp
Вещественное число это как раз бесконечная десятичная дробь. А предел последовательности мы посчитать не можем пока у нас нет определения вещественного числа.
saaivs
бесконечная десятичная дробь — это скорее один из спосбов представления вещественных чисел с некоторой точностью, но не всегда сами эти числа(в смысле точности до изоморфизма)
А аксиоматически определить вещественные числа труда не составляет.
0xd34df00d
Это довольно странный тезис для меня, в частности, из-за упомянутой рядом конструкции по повышению мощности модели.
saaivs
Не очень понял, что вы имеете ввиду. С точки зрения математики форма представления чисел абсолютно неважна. Дестятичное представление по определению есть не более чем одна из множества таких форм. Или о чём вы?
0xd34df00d
Есть бесконечно много структур, на которых выполняются аксиомы, характеризующие вещественные числа (и которые вы не сможете отличить друг от друга «изнутри» этих аксиом), и которые при этом имеют любую наперёд заданную мощность (и которые, соответственно, физически не могут быть изоморфны друг другу).
mayorovp
А пример привести можете? У меня вот не так давно не получилось...
0xd34df00d
Ну берёте обычное R и строите его нестандартный аналог R*. Для получившегося R* можете ещё раз поднять мощность, и так можете делать много-много раз.
Кстати, то ли я что-то фундаментально не понимаю, то ли существует вышеупомянутое непрерывное упорядоченное поле, но счётной мощности (теорема о понижении). Да и было бы интересно посмотреть, полно ли множество вычислимых вещественных чисел или нет, но у меня недостаточно интуиции в нужных для этого вещах.
mayorovp
А является ли R* полем?
Q не является непрерывным. Более того, любое упорядоченное поле будет содержать Q, а непрерывное замыкание Q даёт R.
0xd34df00d
Да, это элементарное расширение R, поэтому на нём по определению (ну или по построению) выполняются все те же высказывания (логики первого порядка), что и на R.
Так и я не говорил о Q, и не говорил, что любое счётное множество непрерывно.
mayorovp
Так ведь непрерывность — одна из аксиом вещественных чисел.
А можно подробности?
0xd34df00d
Если вкратце, то на вики вроде неплохо написано, судя по беглому просмотру.
Собственно, с одной стороны,
С другой, там же:
Разумно, и я изначально об этом и не подумал — понятие подмножества (требуемое для аксиоматизации полноты) эквивалентно кванторам по предикатам, что ломает применимость теоремы Левенгейма-Сколема.
Спасибо, что дали повод поковырять.
saaivs
Практически всё сказанное в этом тезисе, мягко говоря, неверно. Ну, или я вас и со второго раза не понял.
Множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле. (см. пример доказательства)
0xd34df00d
Мы это чуть дальше в комментариях выяснили: упомянутая теорема, конструирующая эти структуры, в данном случае неприменима, так как для построения вещественных чисел логики первого порядка недостаточно (про что я напрочь забыл).
saaivs
Ага, прочитал)… но, как водится, после.
0xd34df00d
Да, есть понятие вычислимого вещественного числа, для которого существует алгоритм, и таких чисел счётное число. Все интересные на практике числа вычислимы (включая всякие там корни из двух, пи, е и так далее), но есть бесконечно много невычислимых чисел. Показать на них пальцем конструктивно не получится по определению.
ildarz
Нет, потому что слово — конечная последовательность символов, а вещественные числа записываются бесконечными.
saaivs
Не все, а некоторые. Например, все целые и рациональные числа, которые очевидно являются так же и вещественными не требуют для своей записи бесконечной последовательности символов. Более того, формально можно даже рассматривать и строки «произвольной длины» — n, если аналитически задать выражение от n, а n устремить к бесконечности.
Собственно о том и речь, что как буд-то получается, что даже имея возможность записать некоторое вещественное число с бесконечной точностью, то у вас это всё равно не получится, т.к. среди вещественных существует ещё некоторое подмножество континууальной мощности таких чисел, которые множеству записей при помощи цифр конечного алфавита не принадлежат. Вот я и хочу понять, в чём именно я ошибаюсь:)
Sayonji
Ваше доказательство счетности всех последвательностей неверно, потому что ваш алгоритим заполнения не работает. Вы перебираете числа длины 1, потом числа длины 2 и т. п. Потом вы «устремляеете n к бесконечности», тем не менее все числа в вашем S будут конечной длины. Чтобы это увидеть, ответьте, на каком номере итерации алгоритма будет сгененировано число 0.(1) (равное 1/9). Спойлер: такого номера как «бесконечность» в натуральных числах нету. Грубо говоря, вы доказали, что между 0 и 1 рациональных чисел, у которых знаменатель это степень десятки, счетно. Это действительно так.
saaivs
Да, вы правы. Спасибо.
commenter
Но можно ваш подход развернуть против вас.
Допустим, нам нужно сгенерировать рациональное периодическое число. Тогда ответьте, на каком номере итерации алгоритма будет сгененировано число 0.(1) (равное 1/9)? Или другими словами — если можно рассматривать реальные числа как последовательность десятичных знаков, то что мешает удалить из этой последовательности запятую и рассматривать оставшиеся знаки (бесконечное их количество) как натуральное число?
И ещё вопрос — а существует вообще доказательство бесконечной длины реальных чисел? Для рациональных чисел это известно — они периодические и период повторяется бесконечное число раз. А для остальных? Может у них есть период? Но бесконечно большой? Или просто где-то есть конец.
Иррациональные алгебраические числа получаются посредством выполнения алгоритма извлечения корня, но как раз для такого подхода ваш ответ приводит отличное опроврежение в виде «приведите номер шага алгоритма, когда мы получим всё число».
И если вы не приведёте шаг алгоритма, то получается, что генерация алгебраических чисел невозможна, что возвращает нас к двум видам бесконечности, которые используются при опровержении возможности получить натуральное число с бесконечным количеством знаков. Или другими словами — это же опровержение можно использовать для бесконечности длины алгебраических чисел (а заодно и для трансцендентных).
Получается, что либо мы отказываемся от бесконечности «и там и там» (для реальных и для натуральных чисел), либо мы соглашаемся с наличием бесконечности, но тоже «и там и там».
ildarz
Определение натуральных чисел.
Реальных — это каких? Если вы имеете в виду вещественные — то это просто одно из их определений.
commenter
Я конечно понимаю, что здесь царит традиция ленивых рассуждений, но в вашем случае она довела ситуацию до весьма показательного случая.
Вы, в общем-то, возразили против чуть ли не самой известной аксиомы математики (о обесконечности числового ряда). И сослались при этом на саму математику. Как вам доказывать что-то при таком противоречивом наборе аксиом, я не знаю.
ildarz
Брр. Я ни на что не возражал и ничего не доказывал. Вы задали два вопроса, ответы на которые вообще не требуют доказательств (в математическом смысле) — достаточно просто прочитать определения соответствующих понятий. Я на это указал. Если что-то непонятно, попробуйте объяснить, что именно.
Sayonji
Выше ответили.
Выше ответили.
У некоторых есть конец (число 0.3), у некоторых нету (число пи).
Не осилил. Если вы спрашиваете алгоритм нумерования алгебраических чисел, то вот он: перебираю все строки из метаматических операторов, цифр и буквы Х в лексиграфическом порядке. Каждую строку проверяю на то, является ли она валидным уравнением. Если да, и уравнение степени k, то k его корней добавляю в множество всех алгебраических чисел (изначально пустое). Очевидно, что в множестве будут дубликаты, но это ничего страшного, меньше чем счётно все равно не бывает бесконечности (продумывать удаление дубликатов мне сейчас лень). Обратите внимание, что «решать „уравнение не надо (и не возможно). Числа в моём конструкте определяются как Pair<String, int> — кортеж из уравнения и порядкового номера его корня по возрастанию.
Не осилил. И натуральных, и вещественных чисел бесконечно. Одних счётно, других несчётно.
0xd34df00d
Только в силу вышеупомянутого аргумента таки «почти все» (наверное, даже в смысле меры Лебега, но этот раздел математики я не то что не помню, а всегда знал плохо). У вас счётное число чисел с конечной дробью и несчётное — с бесконечной.
Но это так, игра слов для нердов, не обращайте внимания.
Запишите мне 6/7 в виде конечной десятичной дроби, пожалуйста.
saaivs
Не смогу) Ведь формулировка некорректна, хоть и имел в виду«все целые и некоторые рациональные числа» Но, написал, что написал) Вот тут Sayonji указал уже на фактическую ошибку в моих рассуждениях.
technic93
Я думаю любое вещественное число можно сопоставить с последовательностью, например бинарным поиском (на отрезке [0,1]). Кажется эта последовательность и будет двоичной запись. Потом эту последовательность можно перевести в десятичную запись.
ildarz
Ошибку в алгоритме показали, я добавлю об ошибках на уровне определений.
Неважно. Суть в том, что множество "записей" вещественных чисел с помощью алфавита вообще не является "множеством слов над алфавитом", следовательно, ваши ссылки на (2) и все следующие из этого выводы ошибочны.
Произвольная (сколь угодно большая), но конечная длина и бесконечная длина — это принципиально разные понятия.
saaivs
Я бы сделал уточнение, что «конечная», «бесконечная» и «счётная» длина — не совсем равноправные понятия, чтоб их так легко ставить рядом.
«Счётная» — не значит «конечная». Множество натуральных чисел счётно и бесконечно. Бесконечности сами по себе тоже бывают разные. Множества вещественных и натуральных чисел оба бесконечные, но одно «алеф-ноль», а второе «алеф-один».
michael_vostrikov
Как это работает для программы, которая выводит "Press any key for exit" и ждет нажатия any key, даже если мы точно знаем, в какой момент она будет нажата, и подаем это на вход анализатора? По-моему никак.
nin-jin Автор
Никак, машина Тьюринга не умеет в ввод/вывод.