Как мы показали в предыдущих статьях, поверхностные геологические нарушения (линеаменты) могут быть выделены с помощью линейного преобразования Радона (Хафа), в то время как геологическая плотность может быть восстановлена с помощью кольцевого преобразования Радона (Хафа). При использовании пространственной фильтрации исходных данных можно сопоставить длину волны с глубиной и получить трехмерную модель. При этом, кольцевое преобразование имеет понятные ограничения — кольцевые статистики радиусом меньше 3х пикселов недостоверны, так что, скажем, при использовании открытого рельефа всей планеты разрешением 30 м верхние 40 метров (2*30/sqrt(2)) трехмерной модели являются результатом интерполяции. В случае же линейного преобразования мы избавлены от этого ограничения, поскольку анализируем именно выходы глубинных структур на поверхность.
Сегодня мы построим объемную линеаментную модель и сравним ее с плотностной моделью и интерферограмммой сейсмического события из предыдущих статей. Как будет показано, эти модели согласуются между собой и дополняют друг друга.

Сравнение 3D моделей
Сначала напомним ранее рассмотренную модель из статьи Геология XXI века как наука данных о Земле:

Здесь на фрагменте геологической карты США (слева) в середине изучаемой области, обозначенной фиолетовой квадратной рамкой, мы видим субмеридиональную (вертикальную) геологическую границу почти через всю выбранную область и еще несколько границ поменьше. Соответствующие границы раздела мы можем увидеть на интерферограмме.
Для удобного сравнения сопоставим модели аномалий плотности и линеаментов для выбранной области и равной глубины:
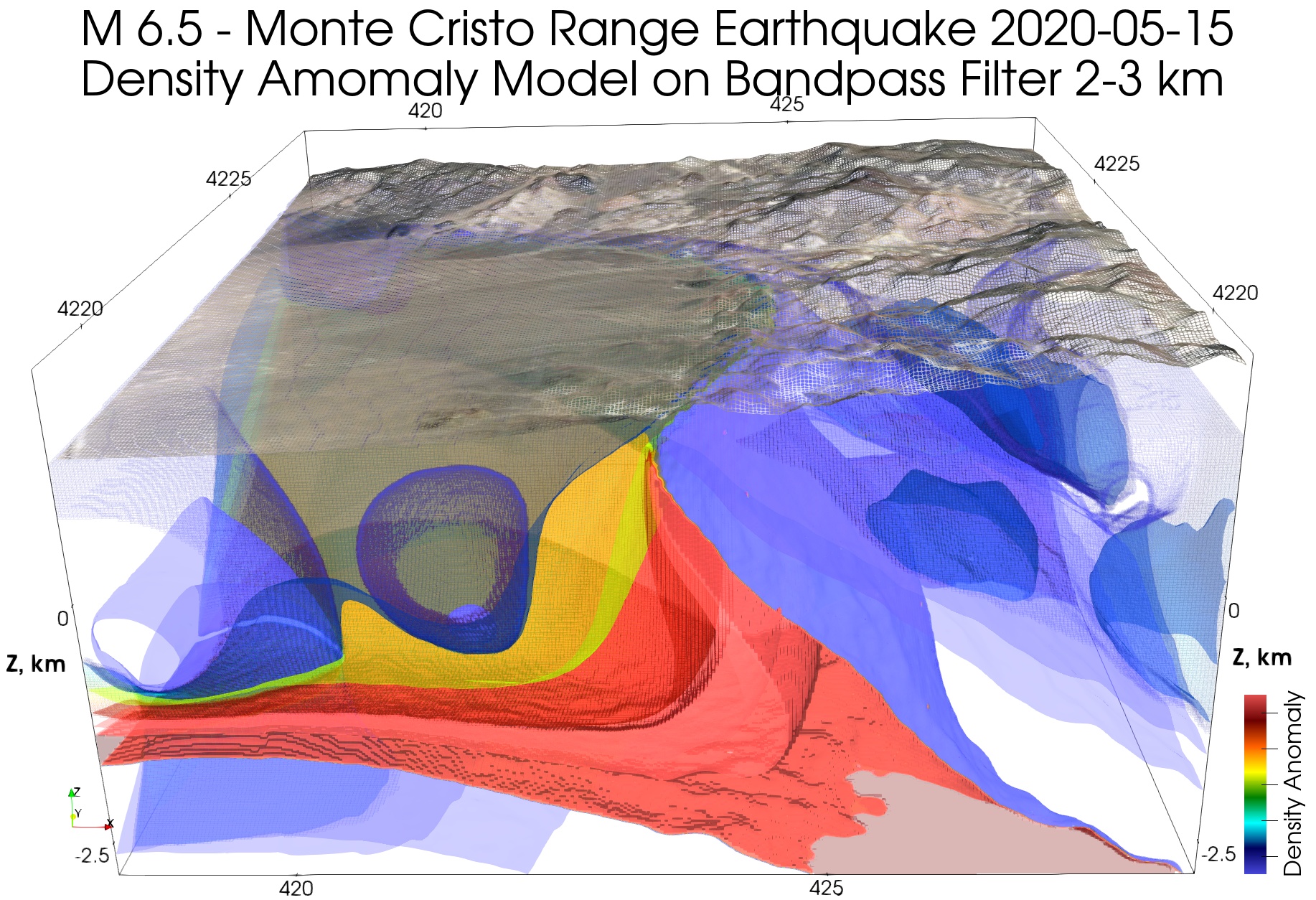
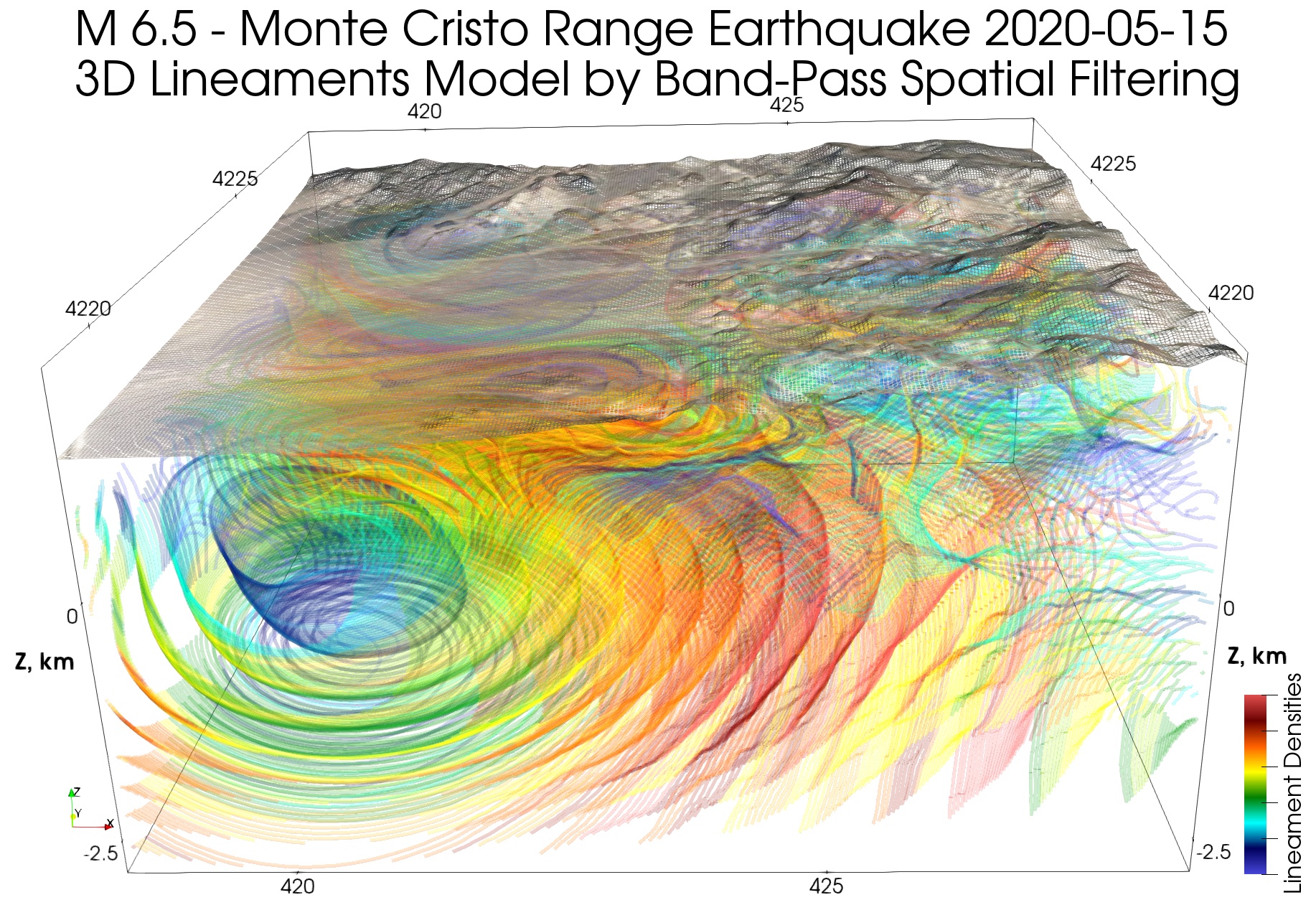
Здесь линеаментная модель намного детальнее у поверхности, что ожидаемо, так как она строится по поверхностным проявлениям. А вот с глубиной детальность линеаментной модели должна снижаться в силу принципа ее построения, поскольку глубина прямо пропорциональна анализируемой поверхностной длине волны (масштабу линеаментов).
Чтобы убедиться в том, где и какая модель точнее, нам достаточно добавить к моделям интерферограмму:

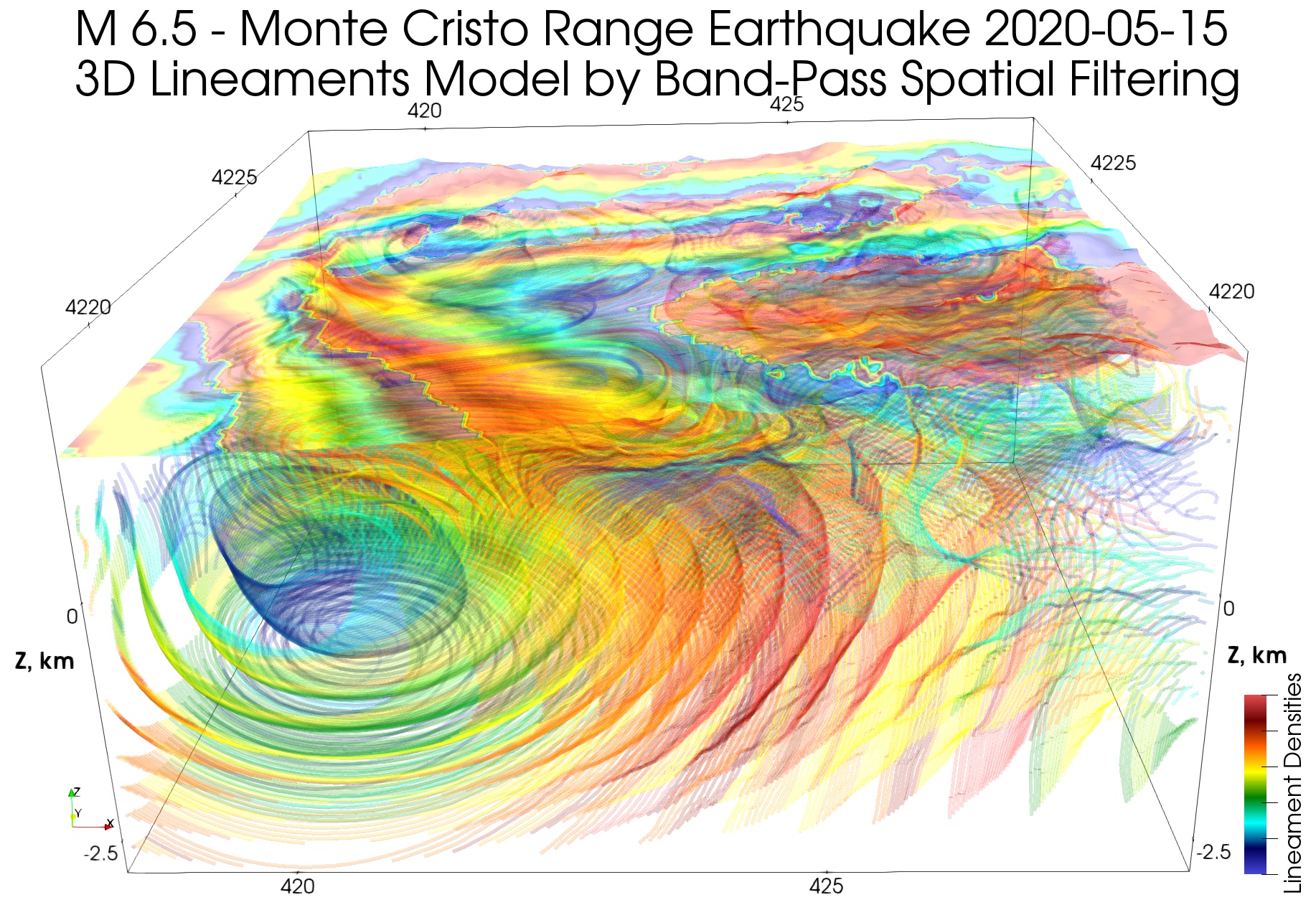
Теперь понятно, что модель плотности у поверхности не точна (как и следует из теории метода), поскольку выступающая часть полукольца интерферограммы в центре модели у поверхности не совпадает с соответствующей границей. Отметим, что смещение здесь составляет около 1-1.5 км, что в точности равно полуширине фильтра (2-3 км). В то же время, показанная на интерферограмме граница в левой части модели -1 — 2 км соответствует модели. На линеаментной модели граница в центре точно соответствует интерферограмме, а вот граница в левой части модели загублена (для одной более крупной структуры здесь на модели плотности выше мы видим две структуры меньшего размера).
Теперь вернемся к розе-диаграмме линеаментов из статьи Динамическая модель линеаментов землетрясения 6.5 баллов в Монте Кристо, Невада, США, где мы анализировали линеаменты лишь от эпицентра землетрясения и до поверхности — то есть те, которые изменяются в процессе землетрясения. Посмотрим теперь более глубокую модель:
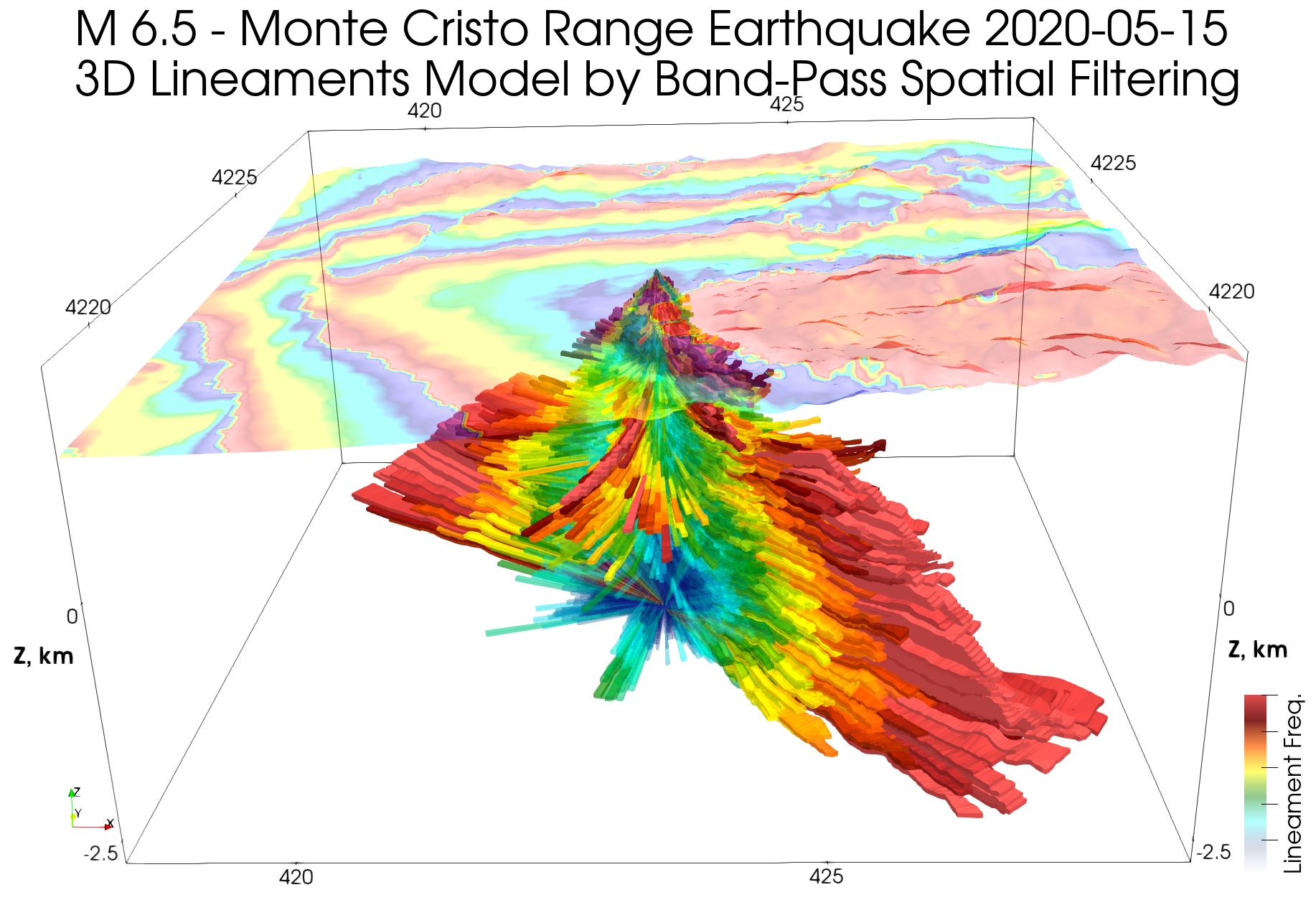
Легко заметить совпадение направления полос на интерферограмме и глубинных линеаментов. Отметим, что на глубине около -2.5 км снова выделяется направление линеаментов, совпадающее с таковым у поверхности, но рассмотрение глубинной динамической модели землетрясения выходит за рамки этой статьи. Сравним эту модель с плотностной, показанной выше:
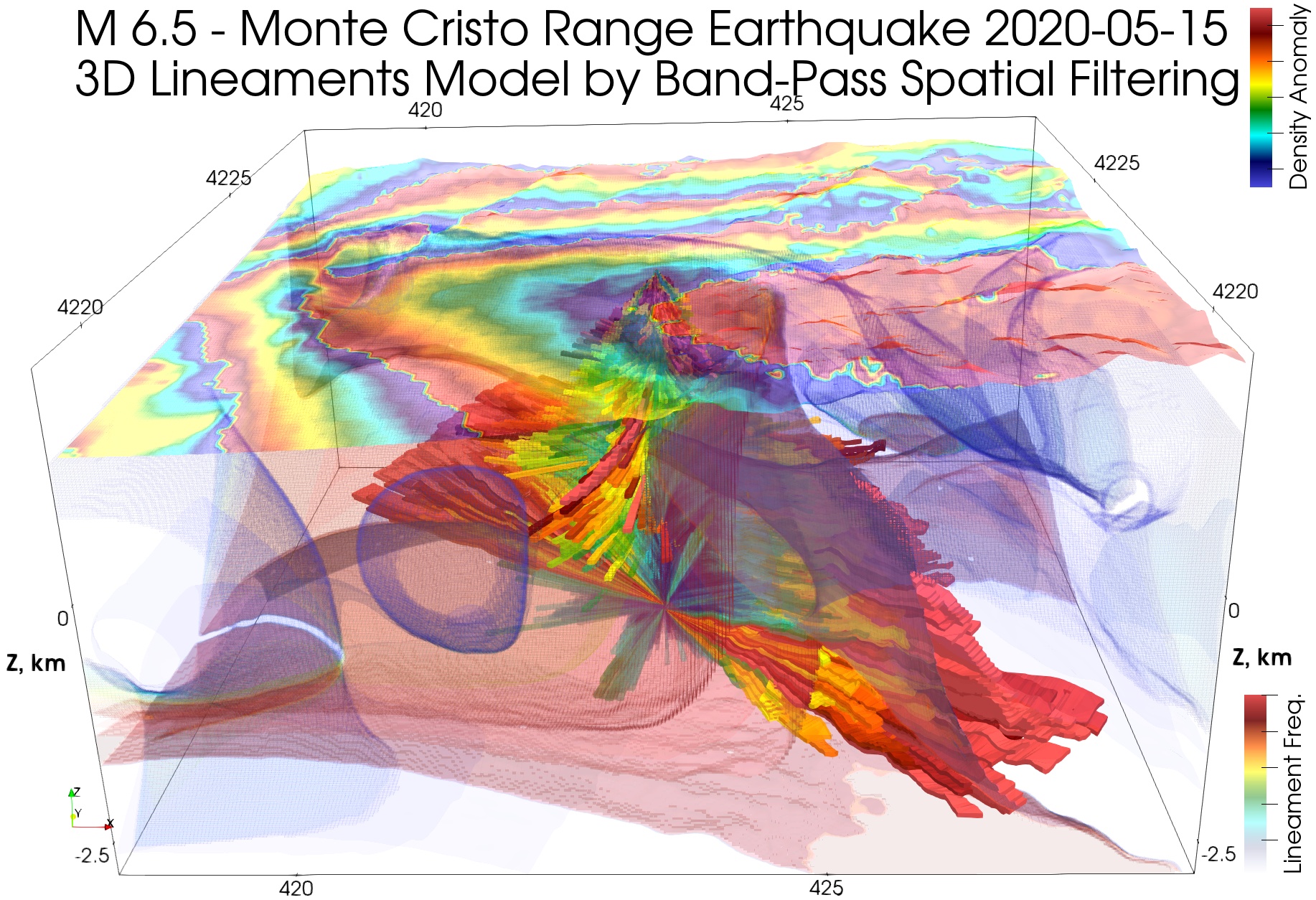
Благодаря тому, что центром модели выбраны координаты эпицентра землетрясения, главное направление розы-диаграммы практически совпадает (с учетом точности плотностной модели; как указано выше, пространственный фильтр 2-3 км соответствует точности 1.5 км) для всех глубин с геологическим разделом модели аномалий плотности. Ранее мы показали, как изменение розы-диаграммы линеаментов позволяет проанализировать геодинамику сейсмического события, а более глубинные структуры, рассматриваемые сейчас, сохраняются. При этом, точность розы-диаграммы с глубиной сохраняется, в отличие от непосредственно 3D линеаментной модели.
Заключение
Мы добрались до самого интересного — совмещения всех ранее рассмотренных методов для решения геологических задач. Как видим, все эти модели согласуются и при этом линеаментная 3D роза-диаграмма визуализирует даже малые смещения и повороты геологических блоков, начиная от поверхности, однако эта модель требует точного позиционирования ее центра. Иначе говоря, трехмерная роза диаграмма совместно анализирует все линеаменты на выбранной площади, не разделяя их пространственно, что позволяет получить точную картину геологических границ и их изменений, но требует дополнительной интерпретации. Детальность 3D линеаментной модели наилучшая у поверхности и убывает с глубиной (при увеличении масштаба пространственного фильтра), в отличие от плотностной модели, которая не определена в приповерхностной области и имеет фиксированную точность (поскольку параметры фильтрации едины для всей модели). Таким образом, эти три модели совместно позволяют получить наиболее полную 4D геодинамическую модель для предсказания будущих сейсмических событий и их последствий.
Для поиска нефти и газа, рудных минералов и питьевой воды нужны точно такие же модели. Отличается только процесс интерпретации — крупные разломы делают бесплодными нефтегазовые коллекторы или являются следствием выхода глубинных геологических блоков (интрузий) на поверхность, а системы мелких трещин становятся путями миграции нефти и газа из фундамента в расположенные выше коллекторы или служат проводниками гидротермальных рудонесущих потоков. Все эти геологические структуры выделяются на обсуждаемых моделях и являются основой для интерпретации геолога или методов машинного обучения, как мы обсуждали в предыдущих статьях.
Как мы последовательно рассматриваем в этом цикле статей, алгоритмы компьютерного зрения, применяемые к физическим величинам (таким, как нарушения поля силы тяжести или рельефа поверхности), позволяют очень быстро и вычислительно корректно решать обратные задачи геофизики. Использование (пространственной) фильтрации для получения однозначно определенного (численного) решения это классический подход радиофизики, который необходим и для геофизики. Таким образом, совершенно проприетарные и чрезвычайно дорогие коммерческие продукты для решения двумерных обратных задач (из-за огромной вычислительной сложности использованных алгоритмов) могут быть заменены открытыми и очень быстрыми методами компьютерного зрения для решения этих же задач в трехмерном виде и построения наглядных геофизических моделей.
P.S. Возможно, у вас возник довольно очевидный вопрос — возможно ли сохранение точности 3D линеаментной модели с глубиной, как и для 3D модели плотности? Да, возможно, но повлечет за собой некоторую потерю точности у поверхности, а на практике линеаментная модель наиболее интересна для дополнения именно приповерхностной области 3D модели плотности.

