Льюис Кэрролл известен миру прежде всего как автор «Алисы в Стране чудес» с необычными волшебными персонажами — Чеширским Котом, Мартовским Зайцем, Птицей Додо, Белым Кроликом и, конечно, загадочным Шалтаем-Болтаем. Однако Льюис Кэрролл кроме популярных детских книжек также написал серьёзные трактаты по аналитической геометрии и линейной алгебре. В юные годы он был зачислен в престижный колледж Оксфордского университета, получил стипендию и должность профессора математики. Достижения Льюиса Кэрролла в области математической логики намного опередили свою эпоху. Он посвящал много времени исследовательской работе, были изданы: «Аналитический разбор пятой книги Евклида», «Конспекты по алгебраической планиметрии», «Элементарное руководство по теории детерминантов», «Евклид и его современные соперники», «Математические курьёзы» и «Символическая логика». Также он увлекался математическими головоломками и интересными задачками.

В одном из выпусков библиотеки журнала «Квант» я обнаружил перевод книги Льюиса Кэрролла «Логическая игра» (The Game of Logic). В этой книге автор рассказывает об оригинальном графическом способе визуализации логических суждений с помощью размеченного особым образом квадратного поля и фишек двух цветов. Этот способ помогает легко оперировать логическими множествами и на основе некоторых предпосылок формулировать новые утверждения. Давайте попробуем разобраться, как это работает.

Немного теории

С помощью метода Льюиса Кэрролла можно оперировать тремя свойствами объекта. Для иллюстрации двух свойств автор предлагает нарисовать квадрат, разделённый на четыре маленьких квадратика. Эти квадратики будут соответствовать наличию или отсутствию у объекта одного из двух свойств — такая маленькая логическая таблица истинности:

• верхний левый квадрат: оба свойства есть;

• верхний правый квадрат: свойство 1 — есть, свойство 2 — отсутствует;

• нижний левый квадрат: свойство 1 — отсутствует, свойство 2 — есть;

• нижний правый квадрат: оба свойства отсутствуют.

Чтобы добавить ещё одно свойство, немного расширим наш исходный квадрат так, чтобы каждый из четырёх маленьких квадратиков имел две области:

• внутреннюю — свойство 3 есть;

• внешнюю — свойство 3 отсутствует.

У нас получилась диаграмма, состоящая из 8 областей, которые соответствуют всем возможным комбинациям наличия или отсутствия у объекта каждого из трёх свойств.

Булочки как объект исследования

Давайте рассмотрим пример. Возьмём какой-нибудь аппетитный объект, например, булочки. Допустим, булочки могут обладать следующими свойствами: свежесть, вкусность и полезность. Тогда для каждого свойства у нас будут пары наличия этого свойства у булочки и его отсутствия:

• свежие — несвежие;

• вкусные — невкусные;

• полезные — вредные.

Пусть внутренний жёлтый квадрат соответствует первым двум свойствам, а внешний — третьему свойству.

Множества у нас есть, теперь нужно описать с помощью этой системы определённые суждения. Для этого будем использовать фишки двух цветов:

• Красная фишка будет означать «некоторые».

• Чёрная фишка будет означать «ни одна».

С помощью размещения фишек на поле мы можем не только иллюстрировать различные глубокомысленные суждения о булочках, но и на основе исходных данных выводить новые суждения — узнавать о булочках что-то новое и поразительное.

Булочки вкусные и свежие

Для начала давайте попробуем проиллюстрировать некоторые суждения, используя только два первых свойства — вкусность и свежесть. Пока мы не будем выходить за пределы внутреннего жёлтого квадрата. Установим логические связи между двумя свойствами булочек. По правилам игры мы можем размещать фишки как в середине маленьких квадратиков, так и на границах между ними.

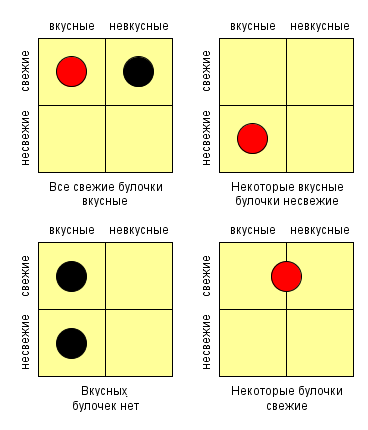
В первой диаграмме мы расположили фишку чёрного цвета на квадратике «свежие и невкусные». Это означает, что таких булочек не существует, ведь чёрная фишка означает «ни одна». А в квадратике «свежие и вкусные» у нас расположена красная фишка. Это означает, что некоторые булочки свежие и вкусные. И, действительно, могут же существовать ещё и несвежие булочки — нижние квадратики. Но для нас важно, что в верхних квадратиках больше нет места. Получается, что установив таким образом фишки, мы однозначно высказались по поводу свежих булочек: они бывают только вкусными!

Во второй диаграмме всё попроще — есть одна красная фишка, которая стоит в нижнем левом квадратике и означает простое утверждение: «Некоторые вкусные булочки несвежие».

На третьей диаграмме в левых квадратиках стоят чёрные фишки. Однозначно и категорично это означает, что вкусных булочек нет. Это специальная диетическая диаграмма.

На четвёртой диаграмме красная фишка установлена на границе между двумя верхними квадратиками. Это значит, что фишка относится ко всей верхней части диаграммы, соответствующей свежести булочек. А вот про вкусность мы ничего определённого сказать не можем. Также мы ничего не знаем о несвежих булочках. Может, они есть, а может их не существует. Получается, что по этой диаграмме мы определённо знаем, что некоторые булочки свежие.

Булочки ещё и полезные

Теперь, чтобы высказать своё авторитетное мнение о полезности булочек, добавим внешний бежевый квадрат.

На первой диаграмме есть две чёрные фишки и одна красная. Если бы у нас был только внутренний жёлтый квадрат, что чёрные фишки нам сообщили бы о том, что невкусных булочек не существует. Но теперь у нас есть ещё и третье свойство — полезность булочек. На нашей диаграмме жёлтый квадрат — это полезные булочки, а бежевый — вредные. Таким образом, мы можем сделать вывод, что невкусных полезных булочек не бывает. Но существуют ли вредные невкусные булочки? На этот вопрос нам даёт ответ красная фишка. Она нам сообщает, что некоторые вредные булочки ещё и невкусные. Объединив всё это вместе, мы можем сказать, что все невкусные булочки вредные. Великолепно!

Вторая диаграмма сообщает нам следующую информацию:

• Нет вредных несвежих булочек.

• Все вкусные несвежие булочки полезны.

Попробуйте самостоятельно разобраться в расположении фишек на этой диаграмме.

От булочек к предикатам

Льюис Кэрролл не просто показывает, как оперировать логическими утверждениями. Книга «Логическая игра» по сути является оригинальным и необычным учебником логики, в которой рассказывается об основных понятиях и законах этой науки. Вот, например, как в книге определено понятие суждения:

Суждение — это предложение, утверждающее, что некоторые или все предметы, принадлежащие определённому классу, называемому субъектом, одновременно являются предметами, принадлежащими другому классу, называемому предикатом (или что ни один предмет, принадлежащий классу «субъект», не является предметом, принадлежащим классу «предикат»).

Автор книги не даст вам заскучать:

Эти девять слов — суждение, признак, термин, суждения, субъект, предикат, частное и общее суждение — окажутся необычайно полезными, если кому-нибудь из ваших приятелей придёт в голову поинтересоваться, не приходилось ли вам когда-нибудь изучать логику. Не забудьте употребить в своём ответе все девять слов, и ваш приятель удалится совершенно потрясённым, «став не только мудрее, но и печальнее».

В суждении «Некоторые свежие булочки суть вкусные булочки» субъект — это «некоторые булочки», а предикат — «вкусные булочки».

Булочный силлогизм

Давайте вернёмся к нашим диаграммам. С помощью несложного правила можно переходить от большой диаграммы к малой — избавляться от третьего свойства в утверждениях. На диаграмме это правило выглядит на удивление просто — если во внешнем квадрате стоит красный кружок, то его можно перенести во внутренний квадрат.

Попробуем разобраться. На первой диаграмме показано, что:

1. Ни одна вкусная булочка не вредная.

2. Некоторые свежие булочки вредные.

Переносим красный кружок во внутренний квадрат и получаем новое утверждение: некоторые свежие булочки невкусные.

Посмотрим внимательно на верхний правый квадратик второй диаграммы. На первой диаграмме к ней примыкает красная фишка. Она нам сообщает, что в принципе в природе существуют свежие невкусные булочки — в рамках второй диаграммы нам не важно, полезные они или вредные. Значит, мы с полным правом можем поставить красную фишку на этот квадратик во второй диаграмме. Про три другие клетки мы ничего определённого сказать не можем, эти клетки на второй диаграмме остаются пустыми.

То, что мы только что проделали, называется силлогизмом — на основе заданных посылок мы сделали заключение. Это только один небольшой пример логических преобразований, которые можно выполнить с помощью диаграмм Льюиса Кэрролла. Чтобы узнать о других возможностях логической игры, предлагаю вам изучить на досуге эту занимательную книгу. Кстати, нашей игре посвящён только первый раздел, а там есть ещё шесть разделов. И, конечно, не забудьте запастись вкусными, свежими и полезными булочками — так читать будет даже интереснее.

• Логическая игра (русский перевод в библиотеке журнала «Квант»).

• The Game of Logic (PDF).