В открытом доступе существует огромное число библиотек для построения моделей машинного обучения в Python. Самые популярные — scikit-learn, XGBoost, LightGBM, Catboost, PyTorch. Каждая из них позволяет построить регрессионную модель для прогнозирования на временных рядах, но для этого требуется преобразование данных и создание новых фичей (feature engineering).

Кроме того, временные ряды требуют своих подходов в оценивании моделей машинного обучения, так как стандартная кросс-валидация не подходит для временных данных. В этой статье мы (я + я) рассмотрим нюансы прогнозирования на практике и с помощью библиотеки skforecast.

Особенности валидации и тестирования моделей на временных рядах

Hold-out тестирование моделей машинного обучения — разбиение данных на тренировочные, валидационные и тестовые (train/val/test split).

• Тренировочные используются для тренировки моделей
• Валидация нужна для выбора гиперпараметров модели
• Тест — для окончательной оценки модели, использующей оптимальные гиперпараметры

При таком подходе модель не должна видеть ни валидационных данных, ни тестовых. После выбора параметров модели, тестовые и валидационные данные можно склеить, обучающая выборка увеличится. При этом, изначальные данные случайно перемешиваются перед разделением для обеспечения несмещенности.

Для временных рядов данный подход не применим, перемешивание приведет к потере временной структуры ряда. В данном случае train/val/test split используется без перемешивания.

Особенности кросс-валидации моделей на временных рядах

Кросс валидация — еще один метод валидации моделей МО. Обычно, когда говорят о кросс-валидации имеют ввиду k-Fold и его модификации. В отличии от Hold-out тестирования данные разбиваются на k одинаковых частей — фолдов. Далее проходит k-итераций, в которых выбирается один из фолдов, модель обучается на k-1 фолде и тестируется на выбранном. Финальная оценка вычисляется усреднением результатов итераций, либо на отложенном тестовом множестве.

Как и в случае с hold-out тестированием, при обычной кросс валидации с временными рядами будет потеряна их внутренняя структура. Поэтому используется вот такая схема:

Источник

Данные разбивают на k-фолдов, только тренировочные фолды обязательно должны идти до валидационных. По мере тестирования, тренировочных данных становится больше.

Существуют так же модификации этого метода, кратко с ними можно познакомиться здесь: ссылка

Метрики

Помимо стандартных метрик MSE и MAE в предсказании временных рядов используются MAPE и WAPE и их модификации.


A (actual) — реальные значения.
F (forecasted) — предсказанные значения.

Практика

Существуют множество библиотек для предсказания временных рядов. Одна из них — skforecast (Документация).

Она предоставляем простой интерфейс sklearn.
Из плюсов этой библиотеки:
1) Легкость использования
2) Поддержка большинства классических моделей МО
3) Большое количество вспомогательных функций (grid_search, cross_validation)
4) Автоматическое создание лаговых параметров для модели

# Импортирование нужных библиотек
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.model_selection import backtesting_forecaster
from skforecast.model_selection import grid_search_forecaster

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error   # Загрузка и обработка данных   
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler 

from catboost import CatBoostRegressor

# данные представляют из себя даты и переменную, колонки - datetime и y
url = (
    'https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast/master/'
    'data/h2o.csv'
)
data = pd.read_csv(url, sep=',', header=0, names=['y', 'datetime']) # Загружаем
data.datetime = pd.to_datetime(data.datetime) # Приводим дату в тип pandas
data = data.set_index('datetime').asfreq('MS').y # Делаем колонку даты индексом, даем ей периодичность месяц ('MS' - month start)
# Задаем обучающие данные
# Обычно предсказание нужно с определенного момента, которое уточняется с заказчиком
# Тут используем обычную hold-out валидацию 
val_start = pd.to_datetime('2004-01-01')
test_start = pd.to_datetime('2006-01-01')
train = data[data.index < val_start]
val = data[(data.index >= val_start) & (data.index < test_start)]
test = data[(data.index >= test_start)]
# Отрисуем данные
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
ax.plot(train, label='train')
ax.plot(val, label='val')
ax.plot(test, label='test')
ax.set_xlabel('Время')
ax.set_ylabel('Предсказываемая переменная')
plt.legend()
plt.show()

# Определяем простейшую модель
linear_forecaster = ForecasterAutoreg(
    regressor=LinearRegression(),
    lags=12
)

# Обучаем модель
linear_forecaster.fit(train)

# Строим прогноз
predictions = linear_forecaster.predict(len(val))

# Печатаем метрики
print(f"MAPE = {mean_absolute_percentage_error(val, predictions)}")
print(f"MAE = {mean_absolute_error(val, predictions)}")
print(f"MSE = {mean_squared_error(val, predictions)}")

Результат:

MAPE = 0.05773219888680609 
MAE = 0.05362243227390879 
MSE = 0.00446558085422573 

# Строим графики
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
ax.plot(train, label='train')
ax.plot(val, label='val')
ax.plot(predictions, label='predicted')
ax.set_xlabel('Время')
ax.set_ylabel('Предсказываемая переменная')
plt.legend()
plt.show()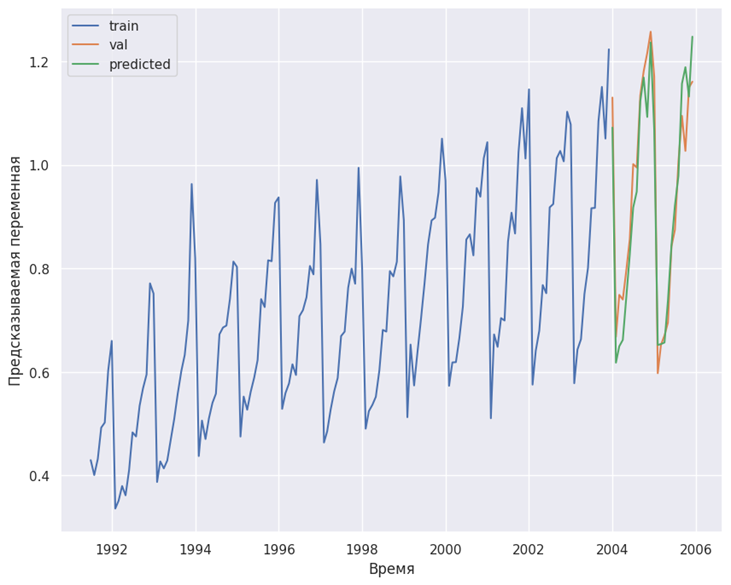

# Еще одной классной функцией является feature_importance
linear_forecaster.get_feature_importances()

# Большой плюс этой библиотеки - она работает с большинством моделей, поддерживающими интерфейс sklearn, например CatBoostRegressor
catboost_forecaster = ForecasterAutoreg(
    regressor=CatBoostRegressor(random_seed=123, verbose=False),
    lags=12
)
catboost_forecaster.fit(train)
predictions = catboost_forecaster.predict(len(val))

print(f"MAPE = {mean_absolute_percentage_error(val, predictions)}")
print(f"MAE = {mean_absolute_error(val, predictions)}")
print(f"MSE = {mean_squared_error(val, predictions)}")

Результат:

MAPE = 0.06647131412453779
MAE = 0.06321521958327374
MSE = 0.005279756555116755

fig, ax = plt.subplots(1, 1, figsize=(10, 8))
ax.plot(train, label='train')
ax.plot(val, label='val')
ax.plot(predictions, label='predicted')
ax.set_xlabel('Время')
ax.set_ylabel('Предсказываемая переменная')
plt.legend()
plt.show()

Как видим, на валидации catboots показал себя даже хуже, чем линейная регрессия! Скорее всего, это происходит из за того что мы используем стандартные параметры модели. Благо, skforecaster поддерживает grid search — автоматический подбор параметров модели

# Создадим модель

catboost_forecaster = ForecasterAutoreg(
    regressor=CatBoostRegressor(random_seed=123, verbose=False),
    lags=1 # Этот параметр будет меняться, поэтому можно поставить его каким угодно
)

lags_grid = [6, 12, [1, 2, 3, 6, 12]] # задаем сетку лагов

param_grid = {
    'n_estimators': [50, 100, 200],
    'max_depth': [5, 10, 15]
}
# Все параметры можно найти в документации, пройдемся по главным:
# forecaster - модель
# y - данные на которых мы хотим учиться
# param_grid, lags_grid - параметры, которые мы хотим тюнить
# steps - горизонт предсказания, на котором мы хотим валидироваться,  нашем случае - len(train)
# initial_train_size - тренировочные данные,  нашем случае - len(train)

# Возвращаемое значение - DataFrame с параметрами и результатом тестирования
results_grid = grid_search_forecaster(
                   forecaster         = catboost_forecaster,
                   y                  = data.loc[:test_start],
                   param_grid         = param_grid,
                   lags_grid          = lags_grid,
                   steps              = len(val),
                   refit              = False,
                   metric             = 'mean_absolute_percentage_error',
                   initial_train_size = len(train),
                   fixed_train_size   = False,
                   return_best        = True,
                   n_jobs             = 'auto', 
                   verbose            = False, 
                   show_progress      = False
               )
results_grid = results_grid.reset_index()

Результат:

Number of models compared: 27.
`Forecaster` refitted using the best-found lags and parameters, and the whole data set: 
  Lags: [ 1  2  3  6 12] 
  Parameters: {'max_depth': 5, 'n_estimators': 50}
  Backtesting metric: 0.05251455987629346

Как видим, в данном случае на валидации Catboost показал себя лучше, MAPE=0.0525. Так же в качестве модели может выступать sklearn Pipeline. Код останется абсолютно тем же, все что поменяется, это параметр regressor в ForecasterAutoreg и param_grid.

pipe = Pipeline(steps=[
    ('scaler', StandardScaler()), 
    ('model', CatBoostRegressor(random_seed=123, verbose=False))
])

catboost_forecaster = ForecasterAutoreg(
    regressor=pipe,
    lags=1 # Этот параметр будет меняться, поэтому можно поставить его каким угодно
)

param_grid = {
    'model__n_estimators': [30 ,50, 100, 200],
    'model__max_depth': [3, 4, 5, 10]
}
# Теперь перетренируем линейную регрессию и catboost на всех обучающих данных и протестируем модели

linear_forecaster = ForecasterAutoreg(
    regressor=LinearRegression(),
    lags=12
)
linear_forecaster.fit(pd.concat([train, val]))
lr_predictions = linear_forecaster.predict(len(test))

print(f"MAPE = {mean_absolute_percentage_error(test, lr_predictions)}")
print(f"MAE = {mean_absolute_error(test, lr_predictions)}")
print(f"MSE = {mean_squared_error(test, lr_predictions)}")

Результат:

MAPE = 0.0733522395192984
MAE = 0.06219065243583432
MSE = 0.005735397594558176

pipe = Pipeline(steps=[
    ('scaler', StandardScaler()), 
    ('model', CatBoostRegressor(**{'max_depth': 5, 'n_estimators': 50}, random_seed=123, verbose=False))
])
catboost_forecaster = ForecasterAutoreg(
    regressor=pipe,
    lags=[1, 2, 3, 6, 12] 
)

catboost_forecaster.fit(pd.concat([train, val]))
cb_predictions  = catboost_forecaster.predict(len(test))

print(f"MAPE = {mean_absolute_percentage_error(test, cb_predictions)}")
print(f"MAE = {mean_absolute_error(test, cb_predictions)}")
print(f"MSE = {mean_squared_error(test, cb_predictions)}")

Результат:

MAPE = 0.05855572171752432
MAE = 0.04682786970015694
MSE = 0.003394050288769456

fig, ax = plt.subplots(1, 1, figsize=(10, 8))
ax.plot(test, label='test', c='black')
ax.plot(lr_predictions, label='lin_reg', ls='--')
ax.plot(cb_predictions, label='Catboost', ls='--')

ax.set_xlabel('Время')
ax.set_ylabel('Предсказываемая переменная')
ax.set_title('Сравнение моделей')
plt.legend()
plt.show()

Заключение

Библиотека skforecast предоставляет удобный инструментарий для работы с временными рядами и упрощает процесс создания и настройки моделей. Она дает возможности для точного и надежного прогнозирования временных данных в различных областях применения.

У этой библиотеки есть еще много достоинств, не упомянутых в статье:
1) С помощью параметра exog в модель можно передавать внешние параметры, такие как время года, день недели и так далее. Это очень полезно во многих случаях.
2) Она поддерживает предсказание на нескольких рядах.

На этой позитивной ноте хочется закончить наше повествование и пригласить всех в комментарии к данной статье. Надеемся, что материал оказался для вас полезным. Спасибо за внимание. Приходите еще.