Всем привет! Мы решили поделится переводом главы «Квантовое время» из книги Шона Кэрролла:
 Что такое время в современном понимании и почему оно обладает именно такими свойствами? Почему время всегда двигается в одном направлении? Почему существуют необратимые процессы? Двадцать лет назад Стивен Хокинг пытался объяснить время через теорию Большого Взрыва. Теперь Шон Кэрролл, один из ведущих физиков-теоретиков современности, познакомит вас с восхитительной парадигмой теории стрелы времени, которая охватывает предметы из энтропии квантовой механики к путешествию во времени в теории информации и смысла жизни.
Что такое время в современном понимании и почему оно обладает именно такими свойствами? Почему время всегда двигается в одном направлении? Почему существуют необратимые процессы? Двадцать лет назад Стивен Хокинг пытался объяснить время через теорию Большого Взрыва. Теперь Шон Кэрролл, один из ведущих физиков-теоретиков современности, познакомит вас с восхитительной парадигмой теории стрелы времени, которая охватывает предметы из энтропии квантовой механики к путешествию во времени в теории информации и смысла жизни.
Книга «Вечность. В поисках окончательной теории времени» не просто следующий шаг на пути к пониманию почему существует Вселенная — это прекрасное чтения для широкого круга читателей, которые интересуются физикой и устройством нашего мира.
Многие из тех, кто в университете прослушал начальный курс физики, могут не согласиться с заявлением о том, что ньютоновскую механику мы понимаем на интуитивном уровне. Единственная ассоциация, которую вызывает у них этот предмет, — это безумная карусель блоков, векторов и наклонных плоскостей, и им никогда бы даже в голову не пришло назвать его «интуитивно понятным».
Однако хотя сам процесс выполнения расчетов в рамках ньютоновской механики — решение домашнего задания или отправка астронавтов на Луну — может быть невыносимо сложным, лежащие в его основе понятия на самом деле довольно просты. Мир сделан из осязаемых вещей, которые мы можем видеть и распознавать: бильярдных шаров, планет, подъемных блоков. Эти вещи оказывают воздействие или сталкиваются друг с другом, и под влиянием подобных воздействий направление и скорость их движения меняются. Если бы демону Лапласа были известны положения и импульсы всех частиц во Вселенной, он мог бы абсолютно точно предсказывать прошлое и будущее. Мы знаем, что это за пределами наших возможностей, однако вполне в наших силах вообразить, что нам известны положения и импульсы нескольких бильярдных шаров на лишенном трения столе, и, по крайней мере в принципе, мы можем представить выполнение соответствующих математических расчетов. После этого дело остается за экстраполяцией и отвагой, и мы сможем объять всю Вселенную.
Физики, желающие подчеркнуть, что это не просто набор каких-то законов, сформулированных Ньютоном, называют ньютоновскую механику «классической» механикой. Классическая механика — это способ мышления о глубинной структуре мира. Разные типы объектов — бейсбольные мячи, молекулы газа, электромагнитные волны — подчиняются разным правилам, но все эти правила по своей структуре однотипны. Суть сходства в том, что у любого объекта есть определенного рода «положение» и определенного рода «импульс», и на основе этой информации можно предсказывать, что будет происходить дальше.
Подобная структура повторяется во множестве контекстов: собственная теория гравитации Ньютона, разработанная Максвеллом теория XIX века об электричестве и магнетизме и общая теория относительности Эйнштейна вписываются в рамки этого шаблона. Класси-ческую механику нельзя назвать еще одной теорией; это парадигма, способ концептуализации сути физической теории, продемонстри-ровавший поразительный масштаб успеха при применении на эмпирическом уровне. После публикации Ньютоном в 1687 году его шедевра Philosophi? Naturalis Principia Mathematica («Математические начала натуральной философии») стало практически невозможно вообразить, что физикой можно заниматься как-то по-другому. Мир сделан из тел, характеризующихся положениями и импульсами, которые перемещаются под воздействием определенных наборов сил; задачей физики было классифицировать эти тела по типам и выяснить, что за силы на них действуют. На этом ее работа должна была быть закончена.
Тем не менее мы с вами уже знаем, что не все так просто и классическая механика неверна. В первые десятилетия XX века физикам, пытающимся разобраться в поведении материи в микроскопических масштабах, пришлось постепенно смириться с мыслью о том, что старые правила придется объявить недействительными и заменить чем-то еще. Этим чем-то еще стала квантовая механика — возможно, величайший триумф человеческого разума и воображения за всю историю. Квантовая механика предлагает картину мира, радикально отличающуюся от картины, создаваемой классической механикой, и ученые никогда всерьез не задумались бы о ней, если бы экспе-риментальные данные не исключали любые другие варианты. Сегодня квантовая механика наслаждается статусом, который с гор-достью носила классическая механика на заре XX века: она с успехом прошла множество эмпирических проверок, и большинство исследователей согласны, что окончательные законы физики должны быть квантово-механическими по природе.
Однако, несмотря на такой триумф, квантовая механика остается чрезвычайно загадочным предметом. Физики полностью доверяют квантовой механике в смысле практического применения: они строят теории, делают предсказания и экспериментально проверяют теоретические результаты, не встречая на этом пути никаких двусмысленностей или неопределенностей. Тем не менее мы до сих пор не можем быть до конца уверены, знаем ли мы, что такое в действительности квантовая механика. Есть одно солидное направление интеллекту альной деятельности, на которое тратят свои силы и время немало талантливых ученых и философов. Это направление известно под названием «интерпретация квантовой механики». Столетие назад не было никакой «интерпретации классической механики» — классическая механика достаточно проста и понятна, для того чтобы ее интерпретация не требовала особых усилий. Но что касается квантовой механики, нам пока неясно, как же правильно думать и говорить о ней.
Эта озабоченность интерпретациями порождается единственным базовым отличием между квантовой механикой и классической механикой, одновременно и кажущимся банальным, и имеющим поистине сокрушительные последствия.
Согласно квантовой механике, то, что мы способны наблюдать в окружающем мире, представляет собой лишь крохотное подмножество того, что на самом деле существует.
Попытки объяснить данный принцип зачастую всего лишь размывают его до полной неузнаваемости. «Это как тот ваш друг с чудесной улыбкой, которого как ни сфотографируешь — улыбка куда-то пропадает». В действительности квантовая механика намного содержа-тельнее. В классическом мире могут возникать сложности с тем, чтобы точно измерить какую-то величину; необходимо соблюдать крайнюю осторожность, чтобы не потревожить изучаемую систему. Однако ничто в классической физике не запрещает нам проявлять такую осторожность. В квантовой механике, с другой стороны, существует непреодолимое препятствие, из-за которого полные и при этом неразрушающие наблюдения физической системы нам недоступны. Это попросту в общем случае невозможно. Что именно происходит, когда вы пытаетесь пронаблюдать за каким-то объектом или системой, и что можно считать фактическим «измерением» — вот основные вопросы. Эта загадка носит крайне полезное название «проблемы измерения» (с тем же успехом «проблемой с машиной» можно было бы назвать ситуацию, когда автомобиль падает с утеса и, пролетая несколько сотен футов, разбивается о скалы на мелкие кусочки). В успешных физических теориях не должно существовать подобных неопределенностей; четкие определения — это главное, что нас в них интересует. Квантовая механика, несмотря на ее несомненную успешность, пока что такого уровня ясности не достигла.
Тем не менее это вовсе не означает, что наука пошла вразнос или что загадками квантовой механики можно оправдывать любые свои убеждения. В частности, квантовая механика не утверждает, что вы способны менять реальность, просто думая о ней, или что современная физика всего лишь заново открыла мудрость древних буддистов. Правила существуют, и мы знаем, как они действуют в условиях, представляющих интерес для нашей повседневной жизни. Однако нам хотелось бы понимать, как эти правила работают в любых ситуациях, какие только можно себе представить.
Большинство современных физиков расправляются с проблемами интерпретации квантовой механики с помощью проверенной веками стратегии «отрицания». Они знают, как правила работают в интересующих их случаях, они могут заставить квантовую механику работать в определенных обстоятельствах и добиться поразительного согласия с экспериментальными данными, и им совершенно не хочется забивать себе голову досадными вопросами о том, что это все означает и можно ли назвать эту теорию абсолютно корректной. Подобная стратегия по большей части вполне отвечает нашим целям в этой книге. Проблема стрелы времени стояла перед Больцманом и его коллегами еще до изобретения квантовой механики, и мы также можем долго и продуктивно рассуждать об энтропии и космологии, не беспокоясь о деталях квантовой механики.
И все же в определенный момент нам придется взглянуть проблеме в лицо. В конце концов, стрела времени — это фундаментальная загадка, и весьма вероятно, что квантовая механика сыграет решающую роль в поиске ответа на нее. Однако есть нечто, представ-ляющее для нас еще больший интерес: тот самый процесс измерения, являющийся средоточием всей интерпретационной неразберихи, обладает примечательным свойством, а именно необратимостью. Один-единственный в толпе общепризнанных и всем известных законов физики, процесс квантового измерения определяет стрелу времени. Однажды выполнив его, вы уже не сможете отменить содеянное. В этом и кроется загадка.
Возможно, эта загадочная необратимость по своей природе аналогична загадочной термодинамической необратимости, описываемой вторым началом: ее создают приближения и отбрасывание информации, тогда как сами по себе фундаментальные физические процессы обратимы. В этой главе я буду отстаивать данную точку зрения. Тем не менее среди экспертов единого мнения по этому вопросу до сих пор нет. Единственное, что не вызывает сомнений, так это необходимость всерьез заниматься проблемой измерений, если нас интересует стрела времени.
Квантовая кошка
Благодаря мысленным экспериментам Эрвина Шрёдингера в научной среде надежно укоренилась традиция при обсуждении квантовой механики ставить опыты на кошках. Кот Шрёдингера был призван иллюстрировать сложности, связанные с проблемой измерения, однако прежде чем углубляться в тонкости, мы потратим немного времени на изучение основ теории. И в наших мысленных экспе-риментах ни одно животное не пострадает.
Представьте себе, что у вашей кошки Китти два любимых места в доме: на диване и под столом в гостиной. В реальном мире сущест-вует бесконечно много положений, которые может занять такой физический объект, как кошка; точно существует бесконечно много значений ее импульса, даже если ваша кошка обычно перемещается по квартире довольно неспешно. Для того чтобы добраться до сути квантовой механики, мы будем все очень сильно упрощать. Так что вообразите, что мы можем полностью описать состояние Китти, как принято в классической механике, просто указав, находится она на диване или под столом. Мы отбрасываем всю информацию о ее скорости, не принимаем во внимание, на какой именно части дивана она лежит, и вообще не учитываем никакие другие положения, не подпадающие под определение «дивана» и «стола». С классической точки зрения мы упрощаем Китти до системы с двумя состояниями. (Системы с двумя состояниями существуют в реальном мире; например, спин электрона или фотона может быть направлен либо вверх, либо вниз. Квантовое состояние системы с двумя состояниями описывается «кубитом» (квантовым битом).)
И здесь мы встречаемся с первым крупным отличием квантовой механики от классической механики: в квантовой механике нет такого понятия, как «местоположение кошки». Классическая механика допускает, что нам не известно, где находится Китти, поэтому мы вправе делать заявления вроде: «Думаю, с вероятностью 75 % она сидит под столом». Однако это всего лишь заявление о нашей неосведомленности, а не о состоянии мира; тот факт, что кошка пребывает в одном из возможных местоположений, неоспорим, и это никак не зависит от того, известно нам об этом или нет.
В квантовой механике не бывает неоспоримых фактов, свидетельствующих о пребывании Китти (или чего угодно еще) в каком-то конкретном месте. Просто-напросто пространство состояний в квантовой механике так не работает. Вместо этого для указания состояний используется штука, известная под названием волновой функции. И волновая функция не дает результатов вроде: «кошка лежит на диване» или «кошка лежит под столом». Она способна сообщать лишь вещи вроде: «если мы поищем, то с вероятностью 75 % обнаружим кошку под столом, а с вероятностью 25 % обнаружим ее на диване».
Отличие «неполного знания» от «фундаментальной квантовой неопределенности» стоит того, чтобы покопаться в нем подольше. Если волновая функция утверждает, что с 75-процентной вероятностью мы найдем кошку под столом, а с 25-процентной — на диване, то значит ли это, что с вероятностью 75 % кошка находится под столом, а с вероятностью 25 % она находится на диване? Нет, такого понятия, как «кошка находится там-то», не существует. Ее квантовое состояние описывается суперпозицией двух разных положений, с которыми мы могли бы работать в классической механике. Суть даже не в том, что оба утверждения одновременно истинны, а в том, что единственно «истинного» местоположения, в котором пребывает кошка, попросту нет. Волновая функция — это лучшее описание реальности кошки, какое только мы в состоянии построить.
Понятно, что согласиться с подобными утверждениями, впервые столкнувшись с ними, очень сложно. И если уж откровенно, наш мир совершенно не кажется нам таким. Когда мы смотрим вокруг, мы видим кошек и планеты и даже электроны, занимающие определен-ные положения, а не в суперпозициях различных положений, описываемых волновыми функциями. Но в этом и кроется секрет волшебства квантовой механики: то, что мы видим, вовсе не обязательно совпадает с реальностью. Волновая функция действительно существует, но мы не в состоянии ее увидеть; мы видим вещи так, словно они находятся в определенных заурядных классических конфигурациях.
Однако это совершенно не означает, что мы не можем полагаться на классическую физику в таких делах, как игра в баскетбол или запуск спутников на орбиту. В квантовой механике не существует «классического предела», в котором объекты ведут себя так, как если бы Ньютон всегда был прав, и этот предел включает в себя весь наш каждодневный опыт. Мы никогда не обнаруживаем объекты макроскопических размеров, такие как кошки, в суперпозициях в форме «75 % здесь, 25 % там»; для них всегда верно «99,9999999 процента (или больше) здесь, 0,0000001 процента (или намного меньше) там». Классическая механика — это приблизительное описание работы макроскопического мира, и это очень хорошее приближение. Реальный мир живет по правилам квантовой механики, однако классической механики более чем достаточно для повседневной жизни. Лишь начав рассматривать атомы и элементарные частицы, мы в полной мере сталкиваемся со следствиями квантовой механики и понимаем, что теперь без нее никуда.
Как работают волновые функции
Вы можете задаваться вопросом: а откуда мы знаем, что написанное выше — правда? В конце концов, какая разница между «существует 75-процентная вероятность увидеть кошку под столом» и «существует 75-процентная вероятность того, что кошка находится под столом». Трудно вообразить эксперимент, который мог бы провести различие между этими вероятностями; в конце концов, единственный способ узнать, где кошка, — посмотреть в ее любимых местах. Однако существует критически важное явление, благодаря которому суть различия становится очевидной. Это квантовая интерференция. Чтобы понять, что это значит, придется запастись терпением и углубиться в детали того, как в действительности работают волновые функции.
В классической механике, где для описания состояния частицы указывают ее положение и импульс, об этом состоянии можно думать как о наборе чисел. Для одной частицы в обычном трехмерном пространстве необходимо указать шесть чисел: положение в каждом из трех направ-лений и импульс в каждом из трех направлений. В квантовой механике состояние описывается волновой функцией, которую также можно пред-ставлять себе как набор чисел. Задача этих чисел — сообщать нам для любого наблюдения или измерения, которое нам только вздумается выполнить, какова вероятность того, что мы получим определенный результат. Таким образом, казалось бы, совершенно естественно полагать, что необходимые нам числа — это самые обыкновенные вероятности: вероятность того, что мы увидим Китти на диване, вероятность того, что мы увидим Китти под столом, и т. д.
Выясняется, однако, что это работает совсем не так. Волновые функции на самом деле схожи с волнами: типичная волновая функция колеблется в пространстве и времени подобно волне на поверхности пруда. Это не совсем очевидно в нашем простом примере, предусмат-ривающем только два возможных результата наблюдений: «на диване» и «под столом». Но если рассмотреть наблюдения с непрерывным множеством возможных исходов, например наблюдение за положением реальной кошки в реальной комнате, то многое сразу же прояснится. Волновая функция похожа на волну на поверхности пруда; единственная разница в том, что это волна в пространстве всех возможных результатов наблюдения: например, всех возможных положений в комнате.
Когда мы видим реальную волну, то замечаем, что относительно поверхности пруда в спокойном состоянии высота воды в волне в разных местах разная. Где-то она выше уровня спокойной воды, а где-то она опускается ниже. Для того чтобы описать волну матема-тически, мы могли бы с каждой точкой пруда связать амплитуду — уровень воды относительно поверхности непотревоженной водной глади. В одних местах амплитуда будет положительной, в других — отрицательной. Волновые функции в квантовой механике работают точно так же. С каждым возможным результатом наблюдения волновая функция связывает число, которое мы называем амплитудой и которое может быть положительным или отрицательным. Полная волновая функция состоит из определенной амплитуды для каждого возможного результата наблюдения; это и есть числа, описывающие состояние в квантовой механике аналогично положениям и импульсам, которые описывают состояние в классической механике. Существует амплитуда, соответствующая пребыванию Китти под столом, и еще одна амплитуда, соответствующая нахождению ее на диване.
При таких условиях у нас остается только одна нерешенная проблема: мы говорим о вероятностях, а вероятность наступления какого-то события никогда не может быть отрицательным числом. Таким образом, нельзя утверждать, что амплитуда, связанная с определенным результатом наблюдения, дает вероятность наступления этого результата; вместо этого должен существовать способ вычисления вероятности, основанный на известном значении амплитуды. К счастью, расчет очень прост! Для того чтобы получить вероятность, нужно взять амплитуду и возвести ее в квадрат:
(вероятность увидеть X) = (амплитуда, связанная с X)2.
Таким образом, если волновая функция Китти связывает амплитуду 0,5 с возможностью увидеть кошку на диване, вероятность на самом деле увидеть ее там равняется (0,5)2 = 0,25, или 25 %. Принципиально важно то, что значение амплитуды могло бы быть отрица-тельным, то есть –0,5, и мы все равно получили бы тот же самый ответ: (–0,5)2 = 0,25. Это может казаться бессмысленным излишеством — две разные амплитуды соответствуют одной и той же физической ситуации, однако выясняется, что наличие положительных и отрицательных значений играет ключевую роль в эволюции состояний в квантовой механике.
Интерференция
Теперь, когда нам известно, что волновые функции могут связывать отрицательные амплитуды с возможными результатами наблюдений, можно вернуться к вопросу, почему мы вообще заговорили о волновых функциях и суперпозициях, вместо того чтобы просто приписать вероятности разным исходам. Причина кроется в интерференции, и эти отрицательные значения необходимы для того, чтобы разобраться, откуда она берется. Мы можем сложить две (отличные от нуля) амплитуды и получить нуль, что было бы невозможно, если бы амплитуды никогда не принимали отрицательные значения.
Для того чтобы понять, как это работает, давайте немного усложним нашу модель кошачьей динамики. Представьте себе, что мы видим, как Китти выходит из спальни на втором этаже. Благодаря нашим предыдущим наблюдениям за ее перемещениями по дому мы собрали достаточно много сведений о том, как действует эта квантовая кошка. Мы знаем, что, стоит ей спуститься на первый этаж, она неминуемо окажется либо на диване, либо под столом и нигде больше (то есть ее конечное состояние представляет собой волновую функцию, описывающую суперпозицию пребы-вания на диване и пребывания под столом). Однако предположим также, что нам известно о существовании двух возможных путей, ведущих от кровати на втором этаже до одного из мест отдыха на первом этаже: Китти сделает остановку либо у миски с кормом, чтобы подкрепиться, либо у когтеточки, чтобы поточить когти. В реальном мире для описания всех этих возможностей достаточно классической механики, но в нашем идеализированном мире мысленного эксперимента мы считаем, что квантовые эффекты играют важную роль.
Теперь посмотрим, какие результаты в действительности дает наше наблюдение. Мы проведем эксперимент двумя разными способами. Во-первых, увидев Китти на первом этаже, мы будем тихонечко следовать за ней, для того чтобы увидеть, по какому маршруту она пойдет: мимо миски с кормом или мимо когтеточки. Вообще-то у нее есть волновая функция, описывающая суперпозицию обеих возможностей, но когда мы проводим фактический эксперимент, мы всегда получаем конкретный результат. Мы ведем себя тише воды ниже травы, и кошка нас совсем не замечает; если хотите, можете даже вообразить, что мы оснастили весь дом шпионскими камерами или лазерными датчиками. Совершенно не важно, с помощью какой технологии мы выясняем, подходит Китти к миске или к когтеточке; главное, что мы пронаблюдали это действие.
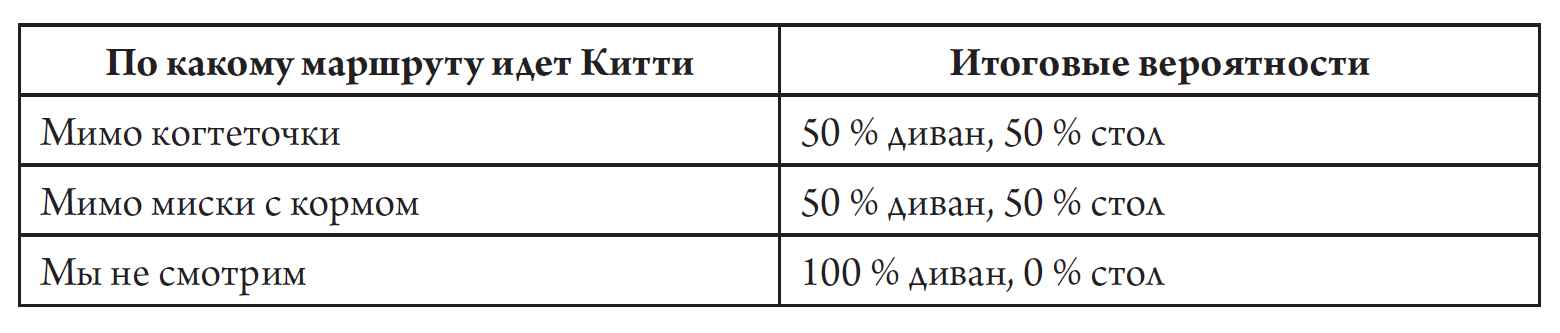
Мы обнаруживаем, что Китти останавливается у миски ровно в половине случаев и точно так же в половине случаев делает остановку у когтеточки (для того чтобы максимально упростить условия, мы предполагаем, что на своем пути к месту отдыха она посещает либо одно место, либо другое, но никогда оба). Ни одно наблюдение, разумеется, само по себе не выявляет волновую функцию; оно позволяет лишь сказать, что в этот конкретный раз мы увидели кошку либо у когтеточки, либо у миски. Но представьте себе, что мы повторяем этот эксперимент очень много раз, и это дает нам возможность делать обоснованные выводы относительно вероятностей этих двух событий.
Однако мы не останавливаемся на этом. Мы позволяем Китти продолжить путь либо на диван, либо под стол, и после того как она устраивается на отдых, мы снова смотрим, какое же место она выбрала. Этот эксперимент мы также повторяем достаточное количество раз, для того чтобы определить вероятности. Теперь мы обнаруживаем, что совершенно неважно, останавливалась она у когтеточки или у миски с кормом; в обоих ситуациях мы видим, что ровно в половине случаев она в итоге приходит на диван, а в половине — под стол, и выбор итогового места отдыха абсолютно не зависит от того, шла она к нему через миску с едой или когтеточку. Очевидно, промежуточный шаг на этом маршруте не играет особой роли; вне зависимости от того, где кошка делает остановку в пути, волновая функция в конце дает равные вероятности для дивана и для стола.
А теперь начинается самое интересное. На этот раз мы вообще не будем смотреть, какой промежуточный шаг Китти делает на своем пути к дивану или столу; нам неинтересно, останавливается она у когтеточки или у миски с кормом. Мы просто ждем, когда она устроится на диване или под столом, а затем проверяем, где она, восстанавливая итоговые вероятности, полученные из волновой функции. Какого результата следует ожидать?
В мире, где царит классическая механика, мы знаем, что должны увидеть. Когда мы шпионили за кошкой, мы были очень осторожны, чтобы наше наблюдение не повлияло на ее действия, и в половине случаев мы обнаруживали ее на диване, а в половине — под столом, независимо от того, по какому маршруту она двигалась. Очевидно, что даже если мы не видим, чем она занимается по пути, это не должно играть никакой роли: в любом случае на последнем шаге у нас есть два исхода с равными вероятностями. Таким образом, даже не наблюдая за промежуточным этапом, мы все равно должны получать одинаковые значения вероятности.
Однако все совсем не так. Это не то, что мы видим в нашем идеализированном мире мысленного эксперимента, где кошка — это настоящий квантовый объект. Когда мы решаем не смотреть, останавливается Китти по пути у миски с едой или у когтеточки, оказывается, что в 100 % случаев в конце она устраивается на отдых на диване! Мы никогда не обнаруживаем ее под столом, то есть финальная волновая функция связывает с этим возможным результатом нулевую амплитуду. Очевидно, что если все это правда, то именно наличие шпионских камер кардинальным образом изменило волновую функцию кошки. Возможные варианты перечислены в таблице ниже.
И это вовсе не исключительно мысленный эксперимент; такой опыт действительно проводился. Не на настоящих кошках, которые, несомненно, относятся к макроскопическим объектам и хорошо описываются в классическом пределе, а на отдельных фотонах в ходе эксперимента, известного под названием «эксперимент с двойной щелью». Есть две щели, через которые может пролететь фотон, и если мы не наблюдаем, через какую щель он пролетает, то получаем одну волновую функцию, а если наблюдаем, то совершенно другую, независимо от того, насколько осторожным и ненавязчивым был контроль.
Вот как это все объясняется. Представим себе, что мы решили проследить, где Китти делает остановку — у миски или у когтеточки, и видим, что она остановилась у когтеточки. Завершив свои дела у когтеточки, она эволюционирует в суперпозицию, где пребывание на диване и пребывание под столом равновероятны. В частности, вследствие особенностей начального состояния Китти и определенных аспектов квантовой кошачьей динамики итоговая волновая функция связывает равные положительные амплитуды с «диваном» и «столом». Теперь рассмотрим другой вариант промежуточного этапа, когда мы видим, что кошка останавливается у миски с едой. В данном случае итоговая волновая функция связывает отрицательную амплитуду со столом, а положительную с диваном — это равные, хотя и противоположные по знаку значения, и, следовательно, соответствующие вероятности абсолютно одинаковы.
Однако если мы не наблюдаем за кошкой и не видим ее на промежуточном этапе — у когтеточки или миски, тогда (в соответствии с природой нашего эксперимента) на этом промежуточном шаге она находится в суперпозиции двух возможностей. В такой ситуации правила квантовой механики предписывают нам сложить два возможных вклада в итоговую волновую функцию: один для маршрута, где Китти останавливается у когтеточки, и второй для маршрута, включающего миску с едой. В обоих случаях амплитуды, соответ-ствующие завершению маршрута на диване, имели положительные значения; таким образом, они усиливают друг друга. Но амплитуды для маршрутов, заканчивающихся под столом, были противоположными по знаку в зависимости от промежуточного шага. То есть при сложении они сокращают друг друга. По отдельности маршруты с любым из двух возможных промежуточных шагов давали нам ненулевую вероятность того, что в конце пути Китти устроится на отдых под столом, но когда одновременно допустимы оба пути (потому что мы не смотрим, по какому она решила пойти), амплитуды интерферируют.
Вот почему волновые функции должны включать отрицательные значения и вот откуда мы знаем, что волновые функции — это «реальные» вещи, а не просто какие-то бухгалтерские инструменты для отслеживания вероятностей.
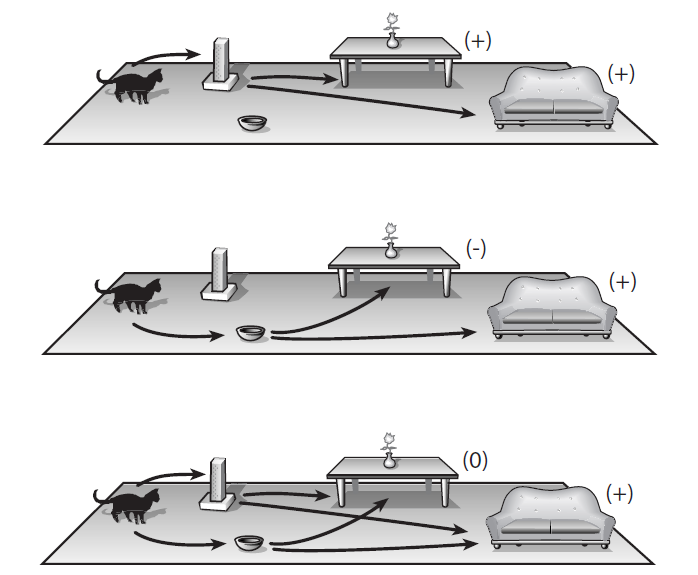
Рис. 11.1. Альтернативные пути эволюции волновой функции Китти. На верхней картинке мы видим, что она остановилась у когте-точки, после чего пойдет либо под стол, либо на диван — у обеих этих возможностей положительные амплитуды. На картинке в центре мы видим, что она подошла к миске с кормом, а оттуда также может отправиться либо под стол, либо на диван, но на этот раз со столом связана отрицательная амплитуда (хотя вероятность все так же больше нуля). Нижняя картинка соответствует ситуации, когда мы не отслеживаем промежуточный шаг ее маршрута, поэтому складываем амплитуды двух допустимых возможностей. В результате мы получаем нулевую амплитуду для стола (так как положительный и отрицательный вклады сокращают друг друга) и положительную амплитуду для дивана
Мы рассмотрели явный случай, когда все вероятности положительны, но итоговая волновая функция получает вклады от двух разных промежуточных шагов, которые сокращают друг друга.
Давайте остановимся на секунду и насладимся тем, насколько глубокомысленно все это выглядит с нашей традиционной точки зрения, зараженной предубеждениями классической механики. Для каждой конкретной реализации эксперимента нам кажется логичным задать вопрос: так где же Китти сделала остановку — у миски с кормом или у когтеточки? Единственный допустимый ответ на этот вопрос — нигде. Она не останавливалась ни там, ни там. Она находилась в суперпозиции обеих возможностей, и нам это известно, потому что обе возможности оказали значительное влияние на амплитуду окончательного ответа.
Реальные кошки — это суетливые макроскопические объекты, состоящие из очень большого числа молекул, и их волновые функции обычно резко локализуются вокруг того, что очень напоминает наше классическое понятие «положения в пространстве». Но на микро-скопическом уровне все эти разговоры о волновых функциях, суперпозициях и интерференции становятся до предела наглядными. Квантовая механика поначалу кажется чем-то жутко непонятным, но это самая суть того, как работают механизмы Природы.
Более подробно с книгой можно ознакомиться на сайте издательства
Оглавление
Отрывок
Для Хаброжителей скидка 25% по купону — Вечность
По факту оплаты бумажной книги отправляем на e-mail электронные версии книг, при покупке электронной книги — все доступные версии отправляются пользователям.
 Что такое время в современном понимании и почему оно обладает именно такими свойствами? Почему время всегда двигается в одном направлении? Почему существуют необратимые процессы? Двадцать лет назад Стивен Хокинг пытался объяснить время через теорию Большого Взрыва. Теперь Шон Кэрролл, один из ведущих физиков-теоретиков современности, познакомит вас с восхитительной парадигмой теории стрелы времени, которая охватывает предметы из энтропии квантовой механики к путешествию во времени в теории информации и смысла жизни.
Что такое время в современном понимании и почему оно обладает именно такими свойствами? Почему время всегда двигается в одном направлении? Почему существуют необратимые процессы? Двадцать лет назад Стивен Хокинг пытался объяснить время через теорию Большого Взрыва. Теперь Шон Кэрролл, один из ведущих физиков-теоретиков современности, познакомит вас с восхитительной парадигмой теории стрелы времени, которая охватывает предметы из энтропии квантовой механики к путешествию во времени в теории информации и смысла жизни.Книга «Вечность. В поисках окончательной теории времени» не просто следующий шаг на пути к пониманию почему существует Вселенная — это прекрасное чтения для широкого круга читателей, которые интересуются физикой и устройством нашего мира.
Квантовое время
Многие из тех, кто в университете прослушал начальный курс физики, могут не согласиться с заявлением о том, что ньютоновскую механику мы понимаем на интуитивном уровне. Единственная ассоциация, которую вызывает у них этот предмет, — это безумная карусель блоков, векторов и наклонных плоскостей, и им никогда бы даже в голову не пришло назвать его «интуитивно понятным».
Однако хотя сам процесс выполнения расчетов в рамках ньютоновской механики — решение домашнего задания или отправка астронавтов на Луну — может быть невыносимо сложным, лежащие в его основе понятия на самом деле довольно просты. Мир сделан из осязаемых вещей, которые мы можем видеть и распознавать: бильярдных шаров, планет, подъемных блоков. Эти вещи оказывают воздействие или сталкиваются друг с другом, и под влиянием подобных воздействий направление и скорость их движения меняются. Если бы демону Лапласа были известны положения и импульсы всех частиц во Вселенной, он мог бы абсолютно точно предсказывать прошлое и будущее. Мы знаем, что это за пределами наших возможностей, однако вполне в наших силах вообразить, что нам известны положения и импульсы нескольких бильярдных шаров на лишенном трения столе, и, по крайней мере в принципе, мы можем представить выполнение соответствующих математических расчетов. После этого дело остается за экстраполяцией и отвагой, и мы сможем объять всю Вселенную.
Физики, желающие подчеркнуть, что это не просто набор каких-то законов, сформулированных Ньютоном, называют ньютоновскую механику «классической» механикой. Классическая механика — это способ мышления о глубинной структуре мира. Разные типы объектов — бейсбольные мячи, молекулы газа, электромагнитные волны — подчиняются разным правилам, но все эти правила по своей структуре однотипны. Суть сходства в том, что у любого объекта есть определенного рода «положение» и определенного рода «импульс», и на основе этой информации можно предсказывать, что будет происходить дальше.
Подобная структура повторяется во множестве контекстов: собственная теория гравитации Ньютона, разработанная Максвеллом теория XIX века об электричестве и магнетизме и общая теория относительности Эйнштейна вписываются в рамки этого шаблона. Класси-ческую механику нельзя назвать еще одной теорией; это парадигма, способ концептуализации сути физической теории, продемонстри-ровавший поразительный масштаб успеха при применении на эмпирическом уровне. После публикации Ньютоном в 1687 году его шедевра Philosophi? Naturalis Principia Mathematica («Математические начала натуральной философии») стало практически невозможно вообразить, что физикой можно заниматься как-то по-другому. Мир сделан из тел, характеризующихся положениями и импульсами, которые перемещаются под воздействием определенных наборов сил; задачей физики было классифицировать эти тела по типам и выяснить, что за силы на них действуют. На этом ее работа должна была быть закончена.
Тем не менее мы с вами уже знаем, что не все так просто и классическая механика неверна. В первые десятилетия XX века физикам, пытающимся разобраться в поведении материи в микроскопических масштабах, пришлось постепенно смириться с мыслью о том, что старые правила придется объявить недействительными и заменить чем-то еще. Этим чем-то еще стала квантовая механика — возможно, величайший триумф человеческого разума и воображения за всю историю. Квантовая механика предлагает картину мира, радикально отличающуюся от картины, создаваемой классической механикой, и ученые никогда всерьез не задумались бы о ней, если бы экспе-риментальные данные не исключали любые другие варианты. Сегодня квантовая механика наслаждается статусом, который с гор-достью носила классическая механика на заре XX века: она с успехом прошла множество эмпирических проверок, и большинство исследователей согласны, что окончательные законы физики должны быть квантово-механическими по природе.
Однако, несмотря на такой триумф, квантовая механика остается чрезвычайно загадочным предметом. Физики полностью доверяют квантовой механике в смысле практического применения: они строят теории, делают предсказания и экспериментально проверяют теоретические результаты, не встречая на этом пути никаких двусмысленностей или неопределенностей. Тем не менее мы до сих пор не можем быть до конца уверены, знаем ли мы, что такое в действительности квантовая механика. Есть одно солидное направление интеллекту альной деятельности, на которое тратят свои силы и время немало талантливых ученых и философов. Это направление известно под названием «интерпретация квантовой механики». Столетие назад не было никакой «интерпретации классической механики» — классическая механика достаточно проста и понятна, для того чтобы ее интерпретация не требовала особых усилий. Но что касается квантовой механики, нам пока неясно, как же правильно думать и говорить о ней.
Эта озабоченность интерпретациями порождается единственным базовым отличием между квантовой механикой и классической механикой, одновременно и кажущимся банальным, и имеющим поистине сокрушительные последствия.
Согласно квантовой механике, то, что мы способны наблюдать в окружающем мире, представляет собой лишь крохотное подмножество того, что на самом деле существует.
Попытки объяснить данный принцип зачастую всего лишь размывают его до полной неузнаваемости. «Это как тот ваш друг с чудесной улыбкой, которого как ни сфотографируешь — улыбка куда-то пропадает». В действительности квантовая механика намного содержа-тельнее. В классическом мире могут возникать сложности с тем, чтобы точно измерить какую-то величину; необходимо соблюдать крайнюю осторожность, чтобы не потревожить изучаемую систему. Однако ничто в классической физике не запрещает нам проявлять такую осторожность. В квантовой механике, с другой стороны, существует непреодолимое препятствие, из-за которого полные и при этом неразрушающие наблюдения физической системы нам недоступны. Это попросту в общем случае невозможно. Что именно происходит, когда вы пытаетесь пронаблюдать за каким-то объектом или системой, и что можно считать фактическим «измерением» — вот основные вопросы. Эта загадка носит крайне полезное название «проблемы измерения» (с тем же успехом «проблемой с машиной» можно было бы назвать ситуацию, когда автомобиль падает с утеса и, пролетая несколько сотен футов, разбивается о скалы на мелкие кусочки). В успешных физических теориях не должно существовать подобных неопределенностей; четкие определения — это главное, что нас в них интересует. Квантовая механика, несмотря на ее несомненную успешность, пока что такого уровня ясности не достигла.
Тем не менее это вовсе не означает, что наука пошла вразнос или что загадками квантовой механики можно оправдывать любые свои убеждения. В частности, квантовая механика не утверждает, что вы способны менять реальность, просто думая о ней, или что современная физика всего лишь заново открыла мудрость древних буддистов. Правила существуют, и мы знаем, как они действуют в условиях, представляющих интерес для нашей повседневной жизни. Однако нам хотелось бы понимать, как эти правила работают в любых ситуациях, какие только можно себе представить.
Большинство современных физиков расправляются с проблемами интерпретации квантовой механики с помощью проверенной веками стратегии «отрицания». Они знают, как правила работают в интересующих их случаях, они могут заставить квантовую механику работать в определенных обстоятельствах и добиться поразительного согласия с экспериментальными данными, и им совершенно не хочется забивать себе голову досадными вопросами о том, что это все означает и можно ли назвать эту теорию абсолютно корректной. Подобная стратегия по большей части вполне отвечает нашим целям в этой книге. Проблема стрелы времени стояла перед Больцманом и его коллегами еще до изобретения квантовой механики, и мы также можем долго и продуктивно рассуждать об энтропии и космологии, не беспокоясь о деталях квантовой механики.
И все же в определенный момент нам придется взглянуть проблеме в лицо. В конце концов, стрела времени — это фундаментальная загадка, и весьма вероятно, что квантовая механика сыграет решающую роль в поиске ответа на нее. Однако есть нечто, представ-ляющее для нас еще больший интерес: тот самый процесс измерения, являющийся средоточием всей интерпретационной неразберихи, обладает примечательным свойством, а именно необратимостью. Один-единственный в толпе общепризнанных и всем известных законов физики, процесс квантового измерения определяет стрелу времени. Однажды выполнив его, вы уже не сможете отменить содеянное. В этом и кроется загадка.
Возможно, эта загадочная необратимость по своей природе аналогична загадочной термодинамической необратимости, описываемой вторым началом: ее создают приближения и отбрасывание информации, тогда как сами по себе фундаментальные физические процессы обратимы. В этой главе я буду отстаивать данную точку зрения. Тем не менее среди экспертов единого мнения по этому вопросу до сих пор нет. Единственное, что не вызывает сомнений, так это необходимость всерьез заниматься проблемой измерений, если нас интересует стрела времени.
Квантовое время
Квантовая кошка
Благодаря мысленным экспериментам Эрвина Шрёдингера в научной среде надежно укоренилась традиция при обсуждении квантовой механики ставить опыты на кошках. Кот Шрёдингера был призван иллюстрировать сложности, связанные с проблемой измерения, однако прежде чем углубляться в тонкости, мы потратим немного времени на изучение основ теории. И в наших мысленных экспе-риментах ни одно животное не пострадает.
Представьте себе, что у вашей кошки Китти два любимых места в доме: на диване и под столом в гостиной. В реальном мире сущест-вует бесконечно много положений, которые может занять такой физический объект, как кошка; точно существует бесконечно много значений ее импульса, даже если ваша кошка обычно перемещается по квартире довольно неспешно. Для того чтобы добраться до сути квантовой механики, мы будем все очень сильно упрощать. Так что вообразите, что мы можем полностью описать состояние Китти, как принято в классической механике, просто указав, находится она на диване или под столом. Мы отбрасываем всю информацию о ее скорости, не принимаем во внимание, на какой именно части дивана она лежит, и вообще не учитываем никакие другие положения, не подпадающие под определение «дивана» и «стола». С классической точки зрения мы упрощаем Китти до системы с двумя состояниями. (Системы с двумя состояниями существуют в реальном мире; например, спин электрона или фотона может быть направлен либо вверх, либо вниз. Квантовое состояние системы с двумя состояниями описывается «кубитом» (квантовым битом).)
И здесь мы встречаемся с первым крупным отличием квантовой механики от классической механики: в квантовой механике нет такого понятия, как «местоположение кошки». Классическая механика допускает, что нам не известно, где находится Китти, поэтому мы вправе делать заявления вроде: «Думаю, с вероятностью 75 % она сидит под столом». Однако это всего лишь заявление о нашей неосведомленности, а не о состоянии мира; тот факт, что кошка пребывает в одном из возможных местоположений, неоспорим, и это никак не зависит от того, известно нам об этом или нет.
В квантовой механике не бывает неоспоримых фактов, свидетельствующих о пребывании Китти (или чего угодно еще) в каком-то конкретном месте. Просто-напросто пространство состояний в квантовой механике так не работает. Вместо этого для указания состояний используется штука, известная под названием волновой функции. И волновая функция не дает результатов вроде: «кошка лежит на диване» или «кошка лежит под столом». Она способна сообщать лишь вещи вроде: «если мы поищем, то с вероятностью 75 % обнаружим кошку под столом, а с вероятностью 25 % обнаружим ее на диване».
Отличие «неполного знания» от «фундаментальной квантовой неопределенности» стоит того, чтобы покопаться в нем подольше. Если волновая функция утверждает, что с 75-процентной вероятностью мы найдем кошку под столом, а с 25-процентной — на диване, то значит ли это, что с вероятностью 75 % кошка находится под столом, а с вероятностью 25 % она находится на диване? Нет, такого понятия, как «кошка находится там-то», не существует. Ее квантовое состояние описывается суперпозицией двух разных положений, с которыми мы могли бы работать в классической механике. Суть даже не в том, что оба утверждения одновременно истинны, а в том, что единственно «истинного» местоположения, в котором пребывает кошка, попросту нет. Волновая функция — это лучшее описание реальности кошки, какое только мы в состоянии построить.
Понятно, что согласиться с подобными утверждениями, впервые столкнувшись с ними, очень сложно. И если уж откровенно, наш мир совершенно не кажется нам таким. Когда мы смотрим вокруг, мы видим кошек и планеты и даже электроны, занимающие определен-ные положения, а не в суперпозициях различных положений, описываемых волновыми функциями. Но в этом и кроется секрет волшебства квантовой механики: то, что мы видим, вовсе не обязательно совпадает с реальностью. Волновая функция действительно существует, но мы не в состоянии ее увидеть; мы видим вещи так, словно они находятся в определенных заурядных классических конфигурациях.
Однако это совершенно не означает, что мы не можем полагаться на классическую физику в таких делах, как игра в баскетбол или запуск спутников на орбиту. В квантовой механике не существует «классического предела», в котором объекты ведут себя так, как если бы Ньютон всегда был прав, и этот предел включает в себя весь наш каждодневный опыт. Мы никогда не обнаруживаем объекты макроскопических размеров, такие как кошки, в суперпозициях в форме «75 % здесь, 25 % там»; для них всегда верно «99,9999999 процента (или больше) здесь, 0,0000001 процента (или намного меньше) там». Классическая механика — это приблизительное описание работы макроскопического мира, и это очень хорошее приближение. Реальный мир живет по правилам квантовой механики, однако классической механики более чем достаточно для повседневной жизни. Лишь начав рассматривать атомы и элементарные частицы, мы в полной мере сталкиваемся со следствиями квантовой механики и понимаем, что теперь без нее никуда.
Как работают волновые функции
Вы можете задаваться вопросом: а откуда мы знаем, что написанное выше — правда? В конце концов, какая разница между «существует 75-процентная вероятность увидеть кошку под столом» и «существует 75-процентная вероятность того, что кошка находится под столом». Трудно вообразить эксперимент, который мог бы провести различие между этими вероятностями; в конце концов, единственный способ узнать, где кошка, — посмотреть в ее любимых местах. Однако существует критически важное явление, благодаря которому суть различия становится очевидной. Это квантовая интерференция. Чтобы понять, что это значит, придется запастись терпением и углубиться в детали того, как в действительности работают волновые функции.
В классической механике, где для описания состояния частицы указывают ее положение и импульс, об этом состоянии можно думать как о наборе чисел. Для одной частицы в обычном трехмерном пространстве необходимо указать шесть чисел: положение в каждом из трех направ-лений и импульс в каждом из трех направлений. В квантовой механике состояние описывается волновой функцией, которую также можно пред-ставлять себе как набор чисел. Задача этих чисел — сообщать нам для любого наблюдения или измерения, которое нам только вздумается выполнить, какова вероятность того, что мы получим определенный результат. Таким образом, казалось бы, совершенно естественно полагать, что необходимые нам числа — это самые обыкновенные вероятности: вероятность того, что мы увидим Китти на диване, вероятность того, что мы увидим Китти под столом, и т. д.
Выясняется, однако, что это работает совсем не так. Волновые функции на самом деле схожи с волнами: типичная волновая функция колеблется в пространстве и времени подобно волне на поверхности пруда. Это не совсем очевидно в нашем простом примере, предусмат-ривающем только два возможных результата наблюдений: «на диване» и «под столом». Но если рассмотреть наблюдения с непрерывным множеством возможных исходов, например наблюдение за положением реальной кошки в реальной комнате, то многое сразу же прояснится. Волновая функция похожа на волну на поверхности пруда; единственная разница в том, что это волна в пространстве всех возможных результатов наблюдения: например, всех возможных положений в комнате.
Когда мы видим реальную волну, то замечаем, что относительно поверхности пруда в спокойном состоянии высота воды в волне в разных местах разная. Где-то она выше уровня спокойной воды, а где-то она опускается ниже. Для того чтобы описать волну матема-тически, мы могли бы с каждой точкой пруда связать амплитуду — уровень воды относительно поверхности непотревоженной водной глади. В одних местах амплитуда будет положительной, в других — отрицательной. Волновые функции в квантовой механике работают точно так же. С каждым возможным результатом наблюдения волновая функция связывает число, которое мы называем амплитудой и которое может быть положительным или отрицательным. Полная волновая функция состоит из определенной амплитуды для каждого возможного результата наблюдения; это и есть числа, описывающие состояние в квантовой механике аналогично положениям и импульсам, которые описывают состояние в классической механике. Существует амплитуда, соответствующая пребыванию Китти под столом, и еще одна амплитуда, соответствующая нахождению ее на диване.
При таких условиях у нас остается только одна нерешенная проблема: мы говорим о вероятностях, а вероятность наступления какого-то события никогда не может быть отрицательным числом. Таким образом, нельзя утверждать, что амплитуда, связанная с определенным результатом наблюдения, дает вероятность наступления этого результата; вместо этого должен существовать способ вычисления вероятности, основанный на известном значении амплитуды. К счастью, расчет очень прост! Для того чтобы получить вероятность, нужно взять амплитуду и возвести ее в квадрат:
(вероятность увидеть X) = (амплитуда, связанная с X)2.
Таким образом, если волновая функция Китти связывает амплитуду 0,5 с возможностью увидеть кошку на диване, вероятность на самом деле увидеть ее там равняется (0,5)2 = 0,25, или 25 %. Принципиально важно то, что значение амплитуды могло бы быть отрица-тельным, то есть –0,5, и мы все равно получили бы тот же самый ответ: (–0,5)2 = 0,25. Это может казаться бессмысленным излишеством — две разные амплитуды соответствуют одной и той же физической ситуации, однако выясняется, что наличие положительных и отрицательных значений играет ключевую роль в эволюции состояний в квантовой механике.
Интерференция
Теперь, когда нам известно, что волновые функции могут связывать отрицательные амплитуды с возможными результатами наблюдений, можно вернуться к вопросу, почему мы вообще заговорили о волновых функциях и суперпозициях, вместо того чтобы просто приписать вероятности разным исходам. Причина кроется в интерференции, и эти отрицательные значения необходимы для того, чтобы разобраться, откуда она берется. Мы можем сложить две (отличные от нуля) амплитуды и получить нуль, что было бы невозможно, если бы амплитуды никогда не принимали отрицательные значения.
Для того чтобы понять, как это работает, давайте немного усложним нашу модель кошачьей динамики. Представьте себе, что мы видим, как Китти выходит из спальни на втором этаже. Благодаря нашим предыдущим наблюдениям за ее перемещениями по дому мы собрали достаточно много сведений о том, как действует эта квантовая кошка. Мы знаем, что, стоит ей спуститься на первый этаж, она неминуемо окажется либо на диване, либо под столом и нигде больше (то есть ее конечное состояние представляет собой волновую функцию, описывающую суперпозицию пребы-вания на диване и пребывания под столом). Однако предположим также, что нам известно о существовании двух возможных путей, ведущих от кровати на втором этаже до одного из мест отдыха на первом этаже: Китти сделает остановку либо у миски с кормом, чтобы подкрепиться, либо у когтеточки, чтобы поточить когти. В реальном мире для описания всех этих возможностей достаточно классической механики, но в нашем идеализированном мире мысленного эксперимента мы считаем, что квантовые эффекты играют важную роль.
Теперь посмотрим, какие результаты в действительности дает наше наблюдение. Мы проведем эксперимент двумя разными способами. Во-первых, увидев Китти на первом этаже, мы будем тихонечко следовать за ней, для того чтобы увидеть, по какому маршруту она пойдет: мимо миски с кормом или мимо когтеточки. Вообще-то у нее есть волновая функция, описывающая суперпозицию обеих возможностей, но когда мы проводим фактический эксперимент, мы всегда получаем конкретный результат. Мы ведем себя тише воды ниже травы, и кошка нас совсем не замечает; если хотите, можете даже вообразить, что мы оснастили весь дом шпионскими камерами или лазерными датчиками. Совершенно не важно, с помощью какой технологии мы выясняем, подходит Китти к миске или к когтеточке; главное, что мы пронаблюдали это действие.
Мы обнаруживаем, что Китти останавливается у миски ровно в половине случаев и точно так же в половине случаев делает остановку у когтеточки (для того чтобы максимально упростить условия, мы предполагаем, что на своем пути к месту отдыха она посещает либо одно место, либо другое, но никогда оба). Ни одно наблюдение, разумеется, само по себе не выявляет волновую функцию; оно позволяет лишь сказать, что в этот конкретный раз мы увидели кошку либо у когтеточки, либо у миски. Но представьте себе, что мы повторяем этот эксперимент очень много раз, и это дает нам возможность делать обоснованные выводы относительно вероятностей этих двух событий.
Однако мы не останавливаемся на этом. Мы позволяем Китти продолжить путь либо на диван, либо под стол, и после того как она устраивается на отдых, мы снова смотрим, какое же место она выбрала. Этот эксперимент мы также повторяем достаточное количество раз, для того чтобы определить вероятности. Теперь мы обнаруживаем, что совершенно неважно, останавливалась она у когтеточки или у миски с кормом; в обоих ситуациях мы видим, что ровно в половине случаев она в итоге приходит на диван, а в половине — под стол, и выбор итогового места отдыха абсолютно не зависит от того, шла она к нему через миску с едой или когтеточку. Очевидно, промежуточный шаг на этом маршруте не играет особой роли; вне зависимости от того, где кошка делает остановку в пути, волновая функция в конце дает равные вероятности для дивана и для стола.
А теперь начинается самое интересное. На этот раз мы вообще не будем смотреть, какой промежуточный шаг Китти делает на своем пути к дивану или столу; нам неинтересно, останавливается она у когтеточки или у миски с кормом. Мы просто ждем, когда она устроится на диване или под столом, а затем проверяем, где она, восстанавливая итоговые вероятности, полученные из волновой функции. Какого результата следует ожидать?
В мире, где царит классическая механика, мы знаем, что должны увидеть. Когда мы шпионили за кошкой, мы были очень осторожны, чтобы наше наблюдение не повлияло на ее действия, и в половине случаев мы обнаруживали ее на диване, а в половине — под столом, независимо от того, по какому маршруту она двигалась. Очевидно, что даже если мы не видим, чем она занимается по пути, это не должно играть никакой роли: в любом случае на последнем шаге у нас есть два исхода с равными вероятностями. Таким образом, даже не наблюдая за промежуточным этапом, мы все равно должны получать одинаковые значения вероятности.
Однако все совсем не так. Это не то, что мы видим в нашем идеализированном мире мысленного эксперимента, где кошка — это настоящий квантовый объект. Когда мы решаем не смотреть, останавливается Китти по пути у миски с едой или у когтеточки, оказывается, что в 100 % случаев в конце она устраивается на отдых на диване! Мы никогда не обнаруживаем ее под столом, то есть финальная волновая функция связывает с этим возможным результатом нулевую амплитуду. Очевидно, что если все это правда, то именно наличие шпионских камер кардинальным образом изменило волновую функцию кошки. Возможные варианты перечислены в таблице ниже.
И это вовсе не исключительно мысленный эксперимент; такой опыт действительно проводился. Не на настоящих кошках, которые, несомненно, относятся к макроскопическим объектам и хорошо описываются в классическом пределе, а на отдельных фотонах в ходе эксперимента, известного под названием «эксперимент с двойной щелью». Есть две щели, через которые может пролететь фотон, и если мы не наблюдаем, через какую щель он пролетает, то получаем одну волновую функцию, а если наблюдаем, то совершенно другую, независимо от того, насколько осторожным и ненавязчивым был контроль.
Вот как это все объясняется. Представим себе, что мы решили проследить, где Китти делает остановку — у миски или у когтеточки, и видим, что она остановилась у когтеточки. Завершив свои дела у когтеточки, она эволюционирует в суперпозицию, где пребывание на диване и пребывание под столом равновероятны. В частности, вследствие особенностей начального состояния Китти и определенных аспектов квантовой кошачьей динамики итоговая волновая функция связывает равные положительные амплитуды с «диваном» и «столом». Теперь рассмотрим другой вариант промежуточного этапа, когда мы видим, что кошка останавливается у миски с едой. В данном случае итоговая волновая функция связывает отрицательную амплитуду со столом, а положительную с диваном — это равные, хотя и противоположные по знаку значения, и, следовательно, соответствующие вероятности абсолютно одинаковы.
Однако если мы не наблюдаем за кошкой и не видим ее на промежуточном этапе — у когтеточки или миски, тогда (в соответствии с природой нашего эксперимента) на этом промежуточном шаге она находится в суперпозиции двух возможностей. В такой ситуации правила квантовой механики предписывают нам сложить два возможных вклада в итоговую волновую функцию: один для маршрута, где Китти останавливается у когтеточки, и второй для маршрута, включающего миску с едой. В обоих случаях амплитуды, соответ-ствующие завершению маршрута на диване, имели положительные значения; таким образом, они усиливают друг друга. Но амплитуды для маршрутов, заканчивающихся под столом, были противоположными по знаку в зависимости от промежуточного шага. То есть при сложении они сокращают друг друга. По отдельности маршруты с любым из двух возможных промежуточных шагов давали нам ненулевую вероятность того, что в конце пути Китти устроится на отдых под столом, но когда одновременно допустимы оба пути (потому что мы не смотрим, по какому она решила пойти), амплитуды интерферируют.
Вот почему волновые функции должны включать отрицательные значения и вот откуда мы знаем, что волновые функции — это «реальные» вещи, а не просто какие-то бухгалтерские инструменты для отслеживания вероятностей.
Рис. 11.1. Альтернативные пути эволюции волновой функции Китти. На верхней картинке мы видим, что она остановилась у когте-точки, после чего пойдет либо под стол, либо на диван — у обеих этих возможностей положительные амплитуды. На картинке в центре мы видим, что она подошла к миске с кормом, а оттуда также может отправиться либо под стол, либо на диван, но на этот раз со столом связана отрицательная амплитуда (хотя вероятность все так же больше нуля). Нижняя картинка соответствует ситуации, когда мы не отслеживаем промежуточный шаг ее маршрута, поэтому складываем амплитуды двух допустимых возможностей. В результате мы получаем нулевую амплитуду для стола (так как положительный и отрицательный вклады сокращают друг друга) и положительную амплитуду для дивана
Мы рассмотрели явный случай, когда все вероятности положительны, но итоговая волновая функция получает вклады от двух разных промежуточных шагов, которые сокращают друг друга.
Давайте остановимся на секунду и насладимся тем, насколько глубокомысленно все это выглядит с нашей традиционной точки зрения, зараженной предубеждениями классической механики. Для каждой конкретной реализации эксперимента нам кажется логичным задать вопрос: так где же Китти сделала остановку — у миски с кормом или у когтеточки? Единственный допустимый ответ на этот вопрос — нигде. Она не останавливалась ни там, ни там. Она находилась в суперпозиции обеих возможностей, и нам это известно, потому что обе возможности оказали значительное влияние на амплитуду окончательного ответа.
Реальные кошки — это суетливые макроскопические объекты, состоящие из очень большого числа молекул, и их волновые функции обычно резко локализуются вокруг того, что очень напоминает наше классическое понятие «положения в пространстве». Но на микро-скопическом уровне все эти разговоры о волновых функциях, суперпозициях и интерференции становятся до предела наглядными. Квантовая механика поначалу кажется чем-то жутко непонятным, но это самая суть того, как работают механизмы Природы.
Более подробно с книгой можно ознакомиться на сайте издательства
Оглавление
Отрывок
Для Хаброжителей скидка 25% по купону — Вечность
По факту оплаты бумажной книги отправляем на e-mail электронные версии книг, при покупке электронной книги — все доступные версии отправляются пользователям.
Комментарии (13)

eyedol
26.02.2016 21:05СПб, книга успешно заказана и оплачена в пункте доставки.
Когда можно ожидать эл.версию на e-mail? :)


quverty
У автора есть достаточно активный блог, наверное можно спросить о чём то и его самого.