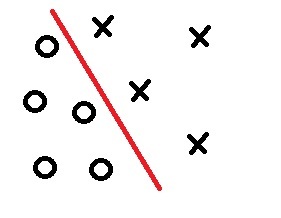
Рисунок 1. двумерный случай
Один из методов, позволяющих решить нашу проблему, это алгоритм наименьшей среднеквадратичной ошибки (НСКО алгоритм).
Интерес данный алгоритм представляет не только в том, что он помогает построить необходимые нам ЛРФ, а в том, что при возникновении ситуации, когда классы линейно неразделимы, мы можем построить ЛРФ, где ошибка неправильной классификации стремится к минимуму.

Рисунок 2. линейно неразделимые классы
Далее перечислим исходные данные:
 — обозначение класса (i — номер класса)
— обозначение класса (i — номер класса) — обучающая выборка
— обучающая выборка — метки( номер класса к которому относится образ
— метки( номер класса к которому относится образ 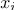 )
) — скорость обучения (произвольная величина)
— скорость обучения (произвольная величина)Этой информации нам более чем достаточно для построения ЛРФ.
Перейдем непосредственно к самому алгоритму.
Алгоритм
1 шаг
а) переводим
 в систему
в систему  , где
, где  равен
равен  , у которого в конце приписан класс образа
, у которого в конце приписан класс образаНапример:
Пусть задан образ
 .
.Тогда
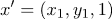 , если
, если  из 1 класса
из 1 класса , если
, если  из 2 класса
из 2 классаб) строим матрицу
 размерностью Nx3 которая состоит из наших векторов
размерностью Nx3 которая состоит из наших векторов 
в) строим

г) считаем
 где
где 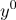 произвольный вектор(по умолчанию единичный)
произвольный вектор(по умолчанию единичный)д)
 (номер итерации)
(номер итерации)2 шаг
Проверяем условие останова:
Если
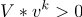 то «СТОП»
то «СТОП»иначе — переходим к шагу 3
3 шаг
а)
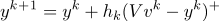 (где + это функция Хэвисайда)
(где + это функция Хэвисайда)Например(функция Хэвисайда):
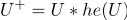
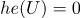 (если
(если 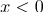 )
)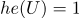 (если
(если 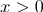 или
или  )
)После подсчетов меняем номер итерации:
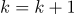
б) переходим на шаг 2
Пример работы алгоритма НСКО

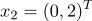
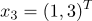
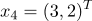
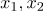 принадлежат 1 классу
принадлежат 1 классу 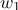
 принадлежат 2 классу
принадлежат 2 классу 
а)




б)

в)

г)
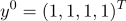
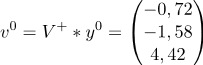
д)

 , т.к. все элементы
, т.к. все элементы 
 «СТОП»
«СТОП»Завершили работу алгоритма, и теперь можно подсчитать нашу ЛРФ.

Спасибо parpalak за онлайн редактор.
Спасибо за внимание.
Комментарии (8)
masai
13.10.2016 19:09+1Какова общая идея метода? Как вычисляется ошибка, которая минимизируется? Почему алгоритм вообще работает? Чем он лучше или хуже других методов классификации? Какова скорость сходимости?
Я правильно понимаю, что первый шаг — это просто решение задачи методом нормального уравнения для подвыборки?
lorc
13.10.2016 19:09+3Как-то это больше похоже на методичку к лабе, честно говоря. Хотелось бы всё-таки увидеть описание работы алгормитма. Хоть какое-то обоснование, почему он сходится и как быстро сходится. Как выбирается скорость обучения… А то сейчас выглядит так, будто если поставить h_k = 100500, то алгоритм всегда будет сходится за одну итерацию.
Короче, хотелось бы видеть полноценную статью, а не короткую заметку.
rocket3
13.10.2016 20:09Спасибо за замечание. Данную тематику можно было бы довести до научного исследования, но в данной статье я постарался изложить теорию кратко, в помощь для тех, кто начинает изучение теории классификации.
masai
13.10.2016 20:40+2При всём уважении, эта статья начинающим вряд ли будет полезна, так как не объясняет область применимости и характер поведения алгоритма.
lorc
13.10.2016 20:43Извините, но теории то как раз нету. Сплошная практика.
Вот вам шаги алгоритма, вот вам пример шагания.


Dark_Daiver
Этот подход чем-то лучше обычных SVM?
rocket3
Метод SVM имеет кардинально иной подход к классификации данных. На практике я не сравнивал, но с точки зрения теории могу сказать, что в случае линейно неразделимых классов в алгоритме SVM предусмотрен переход к пространству большей размерности, дабы получить разделимость, а в НСКО мы, не меняя исходных данных, стараемся разделить классы, сводя ошибку к минимуму.
Dark_Daiver
Ну не обязательно же, достаточно просто перейти от жестких ограничений к мягким. Скажем при помощи Hinge loss.