Постановка задачи
Семантический (смысловой) анализ текста – одна из ключевых проблем как теории создания систем искусственного интеллекта, относящаяся к обработке естественного языка (Natural Language Processing, NLP), так и компьютерной лингвистики. Результаты семантического анализа могут применяться для решения задач в таких областях как, например, психиатрия (для диагностирования больных), политология (предсказание результатов выборов), торговля (анализ востребованности тех или иных товаров на основе комментариев к данному товару), филология (анализ авторских текстов), поисковые системы, системы автоматического перевода. Поисковая машина Google полностью построена на семантическом анализе.
Визуализация результатов семантического анализа является важным этапом его проведения поскольку может обеспечить быстрое и эффективное принятие решений по результатам анализа.
Анализ публикаций в сети по латентно семантическому анализу (LSA) показывает, что визуализация результатов анализа приведена только в двух публикациях [1,2] в виде двух координатного графика семантического пространства с нанесенными координатами слов и документов. Такая визуализация не позволяет однозначно определить группы близких документов и оценить уровень их смысловой связи по принадлежащим документам словам. Хотя в моей публикации под названием “Полный латентно семантический анализ средствами Python” [1] предпринималась попытка использования кластерного анализа результатов латентно семантического анализа, однако были определены только метки кластеров и координаты центроидов для групп слов и документов без визуализации.
Визуализация результатов LSA методом кластерного анализа
Приведём все этапы LSA включая визуализацию результатов методом кластеризации:
- Из анализируемых документов исключаются стоп-слова. Это слова, которые встречаются в каждом тексте и не несут в себе смысловой нагрузки, это, прежде всего, все союзы, частицы, предлоги и множество других слов.
- Из анализируемых документов необходимо отфильтровать цифры, отдельные буквы и знаки препинания.
- Исключить слова, которые встречаются во всех документах только один раз. Это не влияет на конечный результат, но сильно упрощает математические вычисления.
- Со всеми словами из документов должна быть проведена операция стемминга – получение основы слова.
- Составить частотную матрицу индексируемых лов. В этой матрице строки соответствуют индексированным словам, а столбцы — документам. В каждой ячейке матрицы должно быть указано, какое количество, раз слово встречается в соответствующем документе.
- Полученную частотную матрицу следует нормализовать. Стандартный способ нормализации матрицы TF-IDF [3].
- Следующим шагом мы проводим сингулярное разложение полученной матрицы. Сингулярное разложение [4]; – это математическая операция, раскладывающая матрицу на три составляющих. Т.е. исходную матрицу M мы представляем в виде:
M = U*W*V^t
где U и V^t – ортогональные матрицы, а W – диагональная матрица. Причем диагональные элементы матрицы W упорядочены в порядке убывания. Диагональные элементы матрицы W называются сингулярными числами. - Отбросить последние столбцы матрицы U и последние строки матрицы V^t, оставив только первые 2. Это соответственно координаты X, Y каждого слова для матрицы U и координаты X, Y для каждого документа в матрице V^t. Разложение такого вида называют двумерным сингулярным разложением.
- Отбросить последние столбцы матрицы U и последние строки матрицы V^t, оставив только первые 3. Это соответственно координаты X, Y, Z каждого слова для матрицы U и координаты X, Y ,Z для каждого документа в матрице V^t. Разложение такого вида называют трёхмерным сингулярным разложением.
- Подготовка исходных данных в виде вложенных списков координат X, Y для двух столбцов матрицы U слов и двух строк матрицы V^t документов.
- Построение диаграмм евклидовых расстояний меду строками двух столбцов матицы U и столбцами двух строк матрицы V^t.
- Выделение количества кластеров [5,6,7].
- Построение диаграмм и дендрограмм.
- Подготовка исходных данных в виде вложенных списков координат X, Y, Z для трёх столбцов матрицы U слов и трёх строк матрицы V^t документов.
- Выделение количества кластеров.
- Построение диаграмм и дендрограмм.
- Сравнение результатов кластерного анализа для двумерного и трёхмерного сингулярного разложения нормализованной частотной матрицы слов и документов.
Для реализации приведенных этапов была разработана специальная программа, в которой для сравнения использован тот же тестовый набор документов что и в публикации [2].
Программа для визуализации результатов LSA
Результат работы программы
Первые 2 столбца ортогональной матрицы U слов
wikileaks [-0.0741 0.0991]
арестова [-0.023 0.0592]
великобритан [-0.023 0.0592]
вручен [-0.0582 -0.5008]
нобелевск [-0.0582 -0.5008]
основател [-0.0804 0.1143]
полиц [-0.0337 0.0846]
прем [-0.0582 -0.5008]
прот [-0.5954 0.0695]
стран [-0.3261 -0.169 ]
суд [-0.3965 0.1488]
сша [-0.5954 0.0695]
церемон [-0.055 -0.3875]
Первые 2 строки ортогональной матрицы Vt документов
[[ 0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]]
Первые 3 столбца ортогональной матрицы U слов
wikileaks [-0.0741 0.0991 -0.4372]
арестова [-0.023 0.0592 -0.3241]
великобритан [-0.023 0.0592 -0.3241]
вручен [-0.0582 -0.5008 -0.1117]
нобелевск [-0.0582 -0.5008 -0.1117]
основател [-0.0804 0.1143 -0.5185]
полиц [-0.0337 0.0846 -0.4596]
прем [-0.0582 -0.5008 -0.1117]
прот [-0.5954 0.0695 0.1414]
стран [-0.3261 -0.169 0.0815]
суд [-0.3965 0.1488 -0.1678]
сша [-0.5954 0.0695 0.1414]
церемон [-0.055 -0.3875 -0.0802]
Первые 3 строки ортогональной матрицы Vt документов
[[ 0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]
[ 0.5299 -0.0625 0.0797 0.4675 0.1314 0.3714 -0.1979 0.5271 0.1347]]
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy
from numpy import *
import nltk
import scipy
from nltk.corpus import brown
from nltk.stem import SnowballStemmer
from scipy.spatial.distance import pdist
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt
stemmer = SnowballStemmer('russian')
stopwords=nltk.corpus.stopwords.words('russian')
#Тестовый набор документов из коротких новостей
docs =[
"Британская полиция знает о местонахождении основателя WikiLeaks",# Документ № 0
"В суде США начинается процесс против россиянина, рассылавшего спам",# Документ №1
"Церемонию вручения Нобелевской премии мира бойкотируют 19 стран",# Документ №2
"В Великобритании основатель арестован основатель сайта Wikileaks Джулиан Ассандж",# Документ №3
"Украина игнорирует церемонию вручения Нобелевской премии",# Документ №4
"Шведский суд отказался рассматривать апелляцию основателя Wikileaks",# Документ №5
"НАТО и США разработали планы обороны стран Балтии против России",# Документ №6
"Полиция Великобритании нашла основателя WikiLeaks, но, не арестовала",# Документ №7
"В Стокгольме и Осло сегодня состоится вручение Нобелевских премий"# Документ №8
]
word=nltk.word_tokenize((' ').join(docs))# Разбиение всего текста на слова
n=[stemmer.stem(w).lower() for w in word if len(w) >1 and w.isalpha()]#Стемминг всех слов с исключением символов
stopword=[stemmer.stem(w).lower() for w in stopwords]#Стемминг стоп-слов
fdist=nltk.FreqDist(n)
t=fdist.hapaxes()#Слова которые встречаются один раз в тексте
#Построение частотной матрицы А
d={};c=[]
for i in range(0,len(docs)):
word=nltk.word_tokenize(docs[i])
word_stem=[stemmer.stem(w).lower() for w in word if len(w)>1 and w.isalpha()]
word_stop=[ w for w in word_stem if w not in stopword]
words=[ w for w in word_stop if w not in t]
for w in words:
if w not in c:
c.append(w)
d[w]= [i]
elif w in c:
d[w]= d[w]+[i]
a=len(c); b=len(docs)
A = numpy.zeros([a,b])
c.sort()
for i, k in enumerate(c):
for j in d[k]:
A[i,j] += 1
# TF-IDF нормализация матрицы А
wpd = sum(A, axis=0)
dpw= sum(asarray(A > 0,'i'), axis=1)
rows, cols = A.shape
for i in range(rows):
for j in range(cols):
m=float(A[i,j])/wpd[j]
n=log(float(cols) /dpw[i])
A[i,j] =round(n*m,2)
#Сингулярное разложение нормализованной матрицы А
U, S,Vt = numpy.linalg.svd(A)
rows, cols = U.shape
for j in range(0,cols):
for i in range(0,rows):
U[i,j]=round(U[i,j],4)
print('Первые 2 столбца ортогональной матрицы U слов')
for i, row in enumerate(U):
print(c[i], row[0:2])
res1=-1*U[:,0:1]; res2=-1*U[:,1:2]
data_word=[]
for i in range(0,len(c)):# Подготовка исходных данных в виде вложенных списков координат
data_word.append([res1[i][0],res2[i][0]])
plt.figure()
plt.subplot(221)
dist = pdist(data_word, 'euclidean')# Вычисляется евклидово расстояние (по умолчанию)
plt.hist(dist, 500, color='green', alpha=0.5)# Диаграмма евклидовых расстояний
Z = hierarchy.linkage(dist, method='average')# Выделение кластеров
plt.subplot(222)
hierarchy.dendrogram(Z, labels=c, color_threshold=.25, leaf_font_size=8, count_sort=True,orientation='right')
print('Первые 2 строки ортогональной матрицы Vt документов')
rows, cols = Vt.shape
for j in range(0,cols):
for i in range(0,rows):
Vt[i,j]=round(Vt[i,j],4)
print(-1*Vt[0:2, :])
res3=(-1*Vt[0:1, :]);res4=(-1*Vt[1:2, :])
data_docs=[];name_docs=[]
for i in range(0,len(docs)):
name_docs.append(str(i))
data_docs.append([res3[0][i],res4[0][i]])
plt.subplot(223)
dist = pdist(data_docs, 'euclidean')
plt.hist(dist, 500, color='green', alpha=0.5)
Z = hierarchy.linkage(dist, method='average')
plt.subplot(224)
hierarchy.dendrogram(Z, labels=name_docs, color_threshold=.25, leaf_font_size=8, count_sort=True)
#plt.show()
print('Первые 3 столбца ортогональной матрицы U слов')
for i, row in enumerate(U):
print(c[i], row[0:3])
res1=-1*U[:,0:1]; res2=-1*U[:,1:2];res3=-1*U[:,2:3]
data_word_xyz=[]
for i in range(0,len(c)):
data_word_xyz.append([res1[i][0],res2[i][0],res3[i][0]])
plt.figure()
plt.subplot(221)
dist = pdist(data_word_xyz, 'euclidean')# Вычисляется евклидово расстояние (по умолчанию)
plt.hist(dist, 500, color='green', alpha=0.5)#Диаграмма евклидовых растояний
Z = hierarchy.linkage(dist, method='average')# Выделение кластеров
plt.subplot(222)
hierarchy.dendrogram(Z, labels=c, color_threshold=.25, leaf_font_size=8, count_sort=True,orientation='right')
print('Первые 3 строки ортогональной матрицы Vt документов')
rows, cols = Vt.shape
for j in range(0,cols):
for i in range(0,rows):
Vt[i,j]=round(Vt[i,j],4)
print(-1*Vt[0:3, :])
res3=(-1*Vt[0:1, :]);res4=(-1*Vt[1:2, :]);res5=(-1*Vt[2:3, :])
data_docs_xyz=[];name_docs_xyz=[]
for i in range(0,len(docs)):
name_docs_xyz.append(str(i))
data_docs_xyz.append([res3[0][i],res4[0][i],res5[0][i]])
plt.subplot(223)
dist = pdist(data_docs_xyz, 'euclidean')
plt.hist(dist, 500, color='green', alpha=0.5)
Z = hierarchy.linkage(dist, method='average')
plt.subplot(224)
hierarchy.dendrogram(Z, labels=name_docs_xyz, color_threshold=.25, leaf_font_size=8, count_sort=True)
plt.show()
Результат работы программы
Первые 2 столбца ортогональной матрицы U слов
wikileaks [-0.0741 0.0991]
арестова [-0.023 0.0592]
великобритан [-0.023 0.0592]
вручен [-0.0582 -0.5008]
нобелевск [-0.0582 -0.5008]
основател [-0.0804 0.1143]
полиц [-0.0337 0.0846]
прем [-0.0582 -0.5008]
прот [-0.5954 0.0695]
стран [-0.3261 -0.169 ]
суд [-0.3965 0.1488]
сша [-0.5954 0.0695]
церемон [-0.055 -0.3875]
Первые 2 строки ортогональной матрицы Vt документов
[[ 0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]]
Первые 3 столбца ортогональной матрицы U слов
wikileaks [-0.0741 0.0991 -0.4372]
арестова [-0.023 0.0592 -0.3241]
великобритан [-0.023 0.0592 -0.3241]
вручен [-0.0582 -0.5008 -0.1117]
нобелевск [-0.0582 -0.5008 -0.1117]
основател [-0.0804 0.1143 -0.5185]
полиц [-0.0337 0.0846 -0.4596]
прем [-0.0582 -0.5008 -0.1117]
прот [-0.5954 0.0695 0.1414]
стран [-0.3261 -0.169 0.0815]
суд [-0.3965 0.1488 -0.1678]
сша [-0.5954 0.0695 0.1414]
церемон [-0.055 -0.3875 -0.0802]
Первые 3 строки ортогональной матрицы Vt документов
[[ 0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]
[ 0.5299 -0.0625 0.0797 0.4675 0.1314 0.3714 -0.1979 0.5271 0.1347]]
Диаграммы и дендрограмм двумерного сингулярного разложения нормализованной частотной матрицы слов и документов.
Получена чёткая визуализация близости документов (см. docs) и принадлежности слов к документам.
Диаграммы и дендрограмм трёхмерного сингулярного разложения нормализованной частотной матрицы слов и документов.
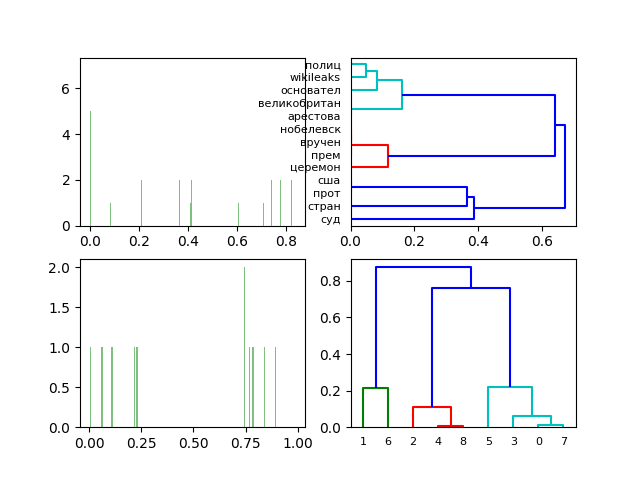
Переход к трёхмерному сингулярному разложению нормализированной частотной матрицы слов и документов для приведенного набора документов (см. docs) качественно не меняет результат анализа LSA.
Выводы
Приведенная методика визуализации LSA, по моему мнению, является удачным дополнением самого LSA и заслуживает внимание разработчиков.
Всем спасибо за внимание!
Ссылки
- Полный латентно семантический анализ средствами Python.
- Латентно-семантический анализ и поиск на Python.
- TF-IDF-Википедия.
- Сингулярное разложение — Википедия.
- Визуализация кластерного анализа в Python (модули hcluster и matplotlib).
- Иерархический кластерный анализ на языке программирование Python.
- Алгоритм k-means [Кластерный анализ и Python].

