Всем привет!
Сегодня хотелось бы рассказать о том, как генерировать лабиринты алгоритмом Эллера, и о том, как сделать красивую 3д визуализацию в Unity, чтобы потом использовать её в своих играх. Также немного рассказать о том, как можно настроить пост обработку внутри данного решения. И по традиции ссылка GitHub с самим генератором.
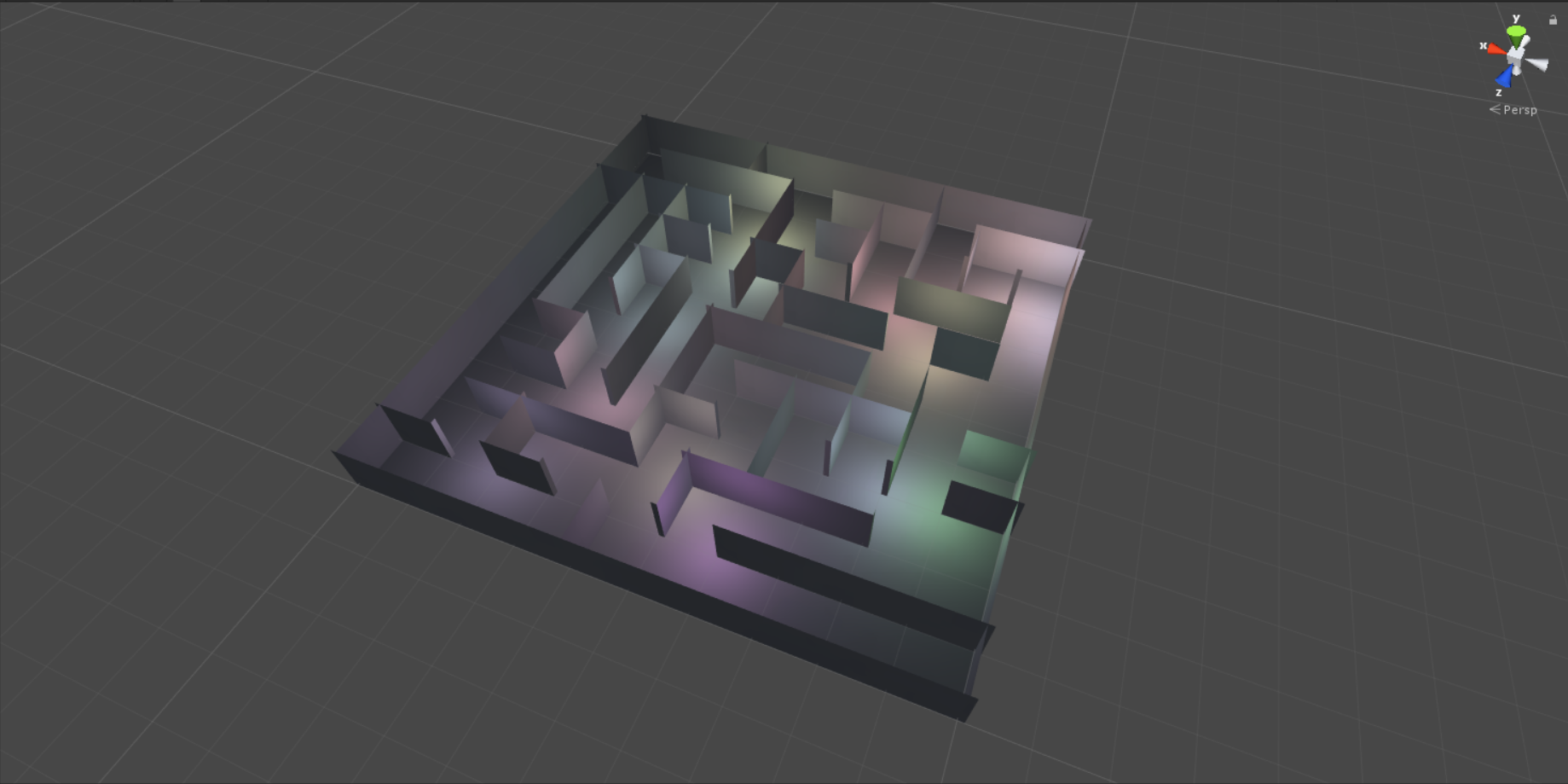
Алгоритм Эллера — это достаточно популярный алгоритм генерации “идеальных” (между двумя точками существует единственный путь) лабиринтов, так как он один из самых быстрых и генерирует “интересные” лабиринты. “Интересными” они получаются за счёт того, что этот алгоритм не базируется на поиске остовного дерева в графе в следствии чего реже генерирует фрактальные структуры. В том числе одним из плюсов алгоритма является то, что он позволяет генерировать лабиринты бесконечного размера за линейное время.
Алгоритм базируется на том, что мы объединяем ячейки лабиринта в разные множества, а в последнем шаге алгоритма объединяем их в одно общем множество. Ячейки находятся в одном множестве — если от одной ячейки можно дойти до другой. Изначально все стены лабиринта подняты, так что все ячейки находятся в разных множествах.
Я видел множество различных описаний самого алгоритма (даже на хабре), поэтому не буду делать этого ещё раз, а вкратце напишу описание своей имплементации.
Сам алгоритм состоит из 3-ёх основных шагов.
В цикле:
1. Обрабатываем строку, случайным образом объединяя ячейки в строке принадлежащие разным множествам.
2. Проходим по той же строке и случайным образом объединяем ячейки из строки выше с нашей строкой (с некоторыми ограничениями)
Последним шагом:
Обрабатываем последнюю строку объединяя ячейки из разных множеств
В целом это и есть алгоритм.
Лабиринт нужно в чём-то хранить. В моём решении есть 2 структуры для хранения лабиринтов.
W4Maze — который по сути представляет из себя массив ячеек 16-ти типов по количеству поднятых стен. Сама ячейка W4Cell хранит в себе просто 4 bool поля, которые говорят о том, какие стены подняты. Эта структура удобна для генерации лабиринта алгоритмом Эллера и удобна для сериализации.
Но с другой стороны она совершенно неудобна для генерации стен. Идея в том, что у лабиринта стены должны обладать толщиной, для того чтобы реализовать подобный алгоритм удобны именно графовые структуры. Для этого была заведена структура MazeGraph и реализовано преобразование из W4Maze в него. Кроме того, для удобства, в нём было создано 2 списка — путей и стен. В итоге написав простенькую визуализацию с помощью Gizmos мы получаем такой лабиринт. Желтый — это стены, а зелёный — это пути.

В целом уже неплохо, но в стенах и путях слишком много лишних узлов, что будет неудобно в дальнейшем для генерации трёхмерной визуализации, так что мы их упрощаем. Это позволит сгенерировать меньше мешей и избежать артефактов освещения на стыках.

Остальное уже дело техники. У меня написан свой инструмент для генерации плоскостей класс MeshTools с самой простой триангуляцией (так как мы знаем порядок добавления точек) В целом можно было бы использовать и юнитёвые Quad’ы, но в любом случае в было бы необходимо пересчитать uv координаты для того, чтобы тайлинг материала на всех стенах был одинаковый и при этом можно было бы использовать один материал. Более подробно можно посмотреть по ссылке на GitHub.

Итак, лабиринт построен, правильно выставлены uv-шки. Теперь хочется показать простейший пример возможности пост процессинга на примере автоматической расстановки света. Для этого я создал класс LightPlacer и тут нам снова пригодится лабиринт W4Maze. Алгоритм пост обработки довольно простой. Мы просто задаём уровни освещённости, переводим тип ячейки в int и принимаем решение, ставить источник света или нет.
И вот наш финальный лабиринт!

С помощью подобной пост обработки можно расставлять декали, врагов, ловушки, да и всё что угодно.
Спасибо за внимание! Кому хочется ознакомится с решением подробнее ссылка на GitHub.
Если кому-то была бы интересна подробнее тема генерации мешей, которая является важной частью решения — могу написать про это отдельной статьёй.
Сегодня хотелось бы рассказать о том, как генерировать лабиринты алгоритмом Эллера, и о том, как сделать красивую 3д визуализацию в Unity, чтобы потом использовать её в своих играх. Также немного рассказать о том, как можно настроить пост обработку внутри данного решения. И по традиции ссылка GitHub с самим генератором.

Алгоритм Эллера — это достаточно популярный алгоритм генерации “идеальных” (между двумя точками существует единственный путь) лабиринтов, так как он один из самых быстрых и генерирует “интересные” лабиринты. “Интересными” они получаются за счёт того, что этот алгоритм не базируется на поиске остовного дерева в графе в следствии чего реже генерирует фрактальные структуры. В том числе одним из плюсов алгоритма является то, что он позволяет генерировать лабиринты бесконечного размера за линейное время.
Алгоритм базируется на том, что мы объединяем ячейки лабиринта в разные множества, а в последнем шаге алгоритма объединяем их в одно общем множество. Ячейки находятся в одном множестве — если от одной ячейки можно дойти до другой. Изначально все стены лабиринта подняты, так что все ячейки находятся в разных множествах.
Я видел множество различных описаний самого алгоритма (даже на хабре), поэтому не буду делать этого ещё раз, а вкратце напишу описание своей имплементации.
Сам алгоритм состоит из 3-ёх основных шагов.
В цикле:
1. Обрабатываем строку, случайным образом объединяя ячейки в строке принадлежащие разным множествам.
Код
private void CreateRow(W4Maze maze, int rowNum)
{
for(int i = 0; i < maze.ColumnCount - 1; i++)
{
var cell = maze.GetCell(i, rowNum);
var nextCell = maze.GetCell(i + 1, rowNum);
if (cell.Set != nextCell.Set)
{
if (UnityEngine.Random.Range(0, 2) > 0)
{
RemoveHorizonWallBetweenCells(
maze,
cell,
nextCell,
rowNum);
}
}
}
}2. Проходим по той же строке и случайным образом объединяем ячейки из строки выше с нашей строкой (с некоторыми ограничениями)
Код
private void CreateVerticalConnections(
W4Maze maze,
int rowNum)
{
bool removeVertical = false;
bool isAddedVertical = false;
for (int i = 0; i < maze.ColumnCount - 1; i++)
{
W4Cell cell = maze.GetCell(i, rowNum);
W4Cell nextCell = maze.GetCell(i + 1, rowNum);
W4Cell topCell = maze.GetCell(i, rowNum + 1);
if (cell.Set != nextCell.Set)
{
if (!isAddedVertical)
{
RemoveVerticalWall(cell, topCell);
}
isAddedVertical = false;
}
else
{
removeVertical = Random.Range(0, 2) > 0;
if (removeVertical)
{
RemoveVerticalWall(cell, topCell);
isAddedVertical = true;
}
}
}
CheckLastVertical(maze, rowNum, isAddedVertical);
}Последним шагом:
Обрабатываем последнюю строку объединяя ячейки из разных множеств
Код
private void CreateLastRow(W4Maze maze)
{
int y = maze.RowCount - 1;
for(int i = 0; i < maze.ColumnCount - 1; i++)
{
var cell = maze.GetCell(i, y);
var nextCell = maze.GetCell(i + 1, y);
if(cell.Set != nextCell.Set)
{
RemoveHorizonWallBetweenCells(
maze,
cell,
nextCell,
y);
}
}
}В целом это и есть алгоритм.
Лабиринт нужно в чём-то хранить. В моём решении есть 2 структуры для хранения лабиринтов.
W4Maze — который по сути представляет из себя массив ячеек 16-ти типов по количеству поднятых стен. Сама ячейка W4Cell хранит в себе просто 4 bool поля, которые говорят о том, какие стены подняты. Эта структура удобна для генерации лабиринта алгоритмом Эллера и удобна для сериализации.
Но с другой стороны она совершенно неудобна для генерации стен. Идея в том, что у лабиринта стены должны обладать толщиной, для того чтобы реализовать подобный алгоритм удобны именно графовые структуры. Для этого была заведена структура MazeGraph и реализовано преобразование из W4Maze в него. Кроме того, для удобства, в нём было создано 2 списка — путей и стен. В итоге написав простенькую визуализацию с помощью Gizmos мы получаем такой лабиринт. Желтый — это стены, а зелёный — это пути.

В целом уже неплохо, но в стенах и путях слишком много лишних узлов, что будет неудобно в дальнейшем для генерации трёхмерной визуализации, так что мы их упрощаем. Это позволит сгенерировать меньше мешей и избежать артефактов освещения на стыках.
К примеру код для стен
private void ProcessWallEdges()
{
for(int i = 0; i < _WallEdges.Count; i++)
{
for(int j = i + 1; j < _WallEdges.Count; j++)
{
var edge1 = _WallEdges[i];
var edge2 = _WallEdges[j];
if (Mathf.Abs(edge1.Normal.x)
== Mathf.Abs(edge2.Normal.x)
&& Mathf.Abs(edge1.Normal.y)
== Mathf.Abs(edge2.Normal.y))
{
if (Edge.IsCanMerge(edge1, edge2))
{
var edge = Edge.Merge(edge1, edge2);
_WallEdges.Remove(edge1);
_WallEdges.Remove(edge2);
_WallEdges.Remove(edge);
_WallEdges.Insert(i, edge);
j = i;
}
}
}
}
}
Остальное уже дело техники. У меня написан свой инструмент для генерации плоскостей класс MeshTools с самой простой триангуляцией (так как мы знаем порядок добавления точек) В целом можно было бы использовать и юнитёвые Quad’ы, но в любом случае в было бы необходимо пересчитать uv координаты для того, чтобы тайлинг материала на всех стенах был одинаковый и при этом можно было бы использовать один материал. Более подробно можно посмотреть по ссылке на GitHub.

Итак, лабиринт построен, правильно выставлены uv-шки. Теперь хочется показать простейший пример возможности пост процессинга на примере автоматической расстановки света. Для этого я создал класс LightPlacer и тут нам снова пригодится лабиринт W4Maze. Алгоритм пост обработки довольно простой. Мы просто задаём уровни освещённости, переводим тип ячейки в int и принимаем решение, ставить источник света или нет.
И снова код
public GameObject SetUpLights(
W4Maze maze,
float height)
{
GameObject lights = new GameObject();
for(int i = 0; i < maze.ColumnCount; i++)
{
for(int j = 0; j < maze.RowCount; j++)
{
var cell = maze.GetCell(i, j);
if(cell.ToInt() < (int) _LightLevel)
{
var lightGo = CreatePointLight();
lightGo.transform.position = new Vector3(
i ,
height * 0.9f,
j);
}
}
}
return lights;
}
public enum LightLevel : byte
{
Low = 3,
Medium = 5,
High = 10,
VeryHigh = 16
}И вот наш финальный лабиринт!

С помощью подобной пост обработки можно расставлять декали, врагов, ловушки, да и всё что угодно.
Спасибо за внимание! Кому хочется ознакомится с решением подробнее ссылка на GitHub.
Если кому-то была бы интересна подробнее тема генерации мешей, которая является важной частью решения — могу написать про это отдельной статьёй.

