Алгоритм коллапса волновой функции (Wavefunction Collapse Algorithm) учит компьютер импровизировать. На входе он получает архетипичные данные и создаёт процедурно генерируемые данные, похожие на исходные.


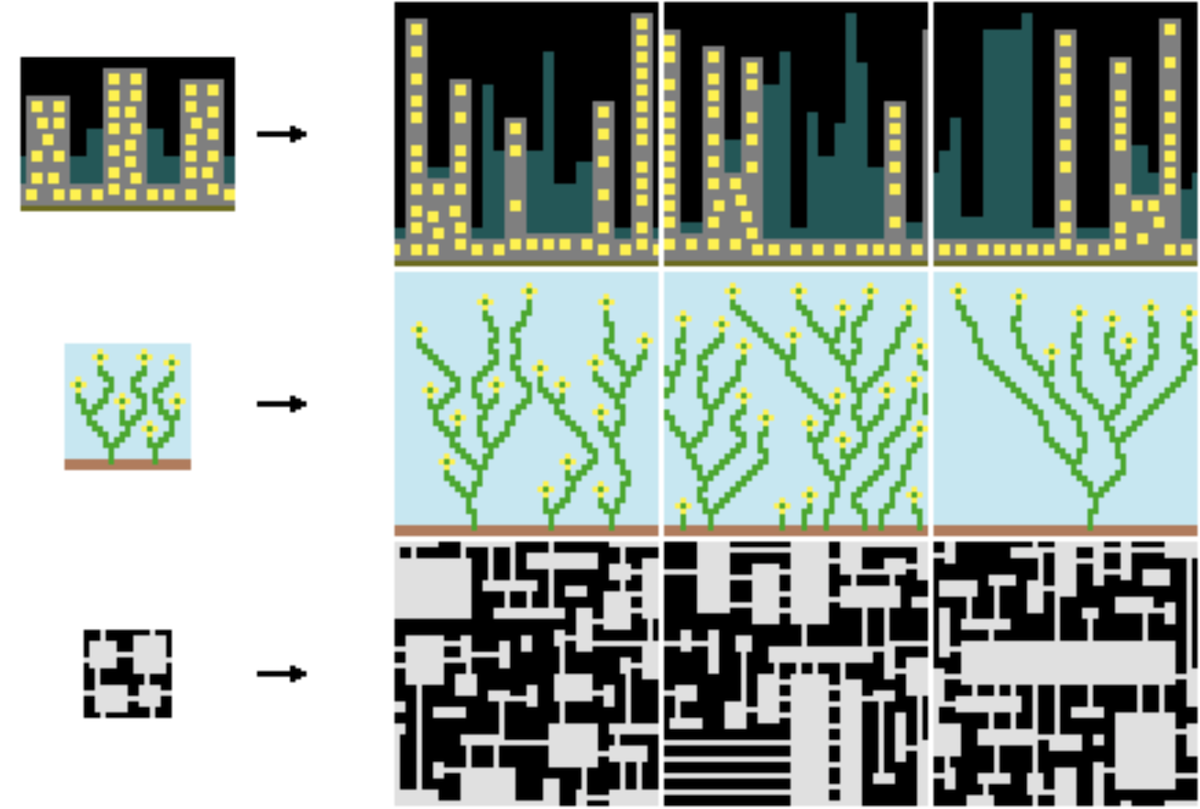
(Источник)

Чаще всего он используется для создания изображений, но может также строить города, скейтпарки и писать ужасные стихи.


(Источник)

Коллапс волновой функции — это очень независимо мыслящий алгоритм, не требующий практически никакой помощи или инструкций извне. Вам нужен только пример стиля, которого нужно достичь, а всё остальное он сделает сам. Несмотря на свою самодостаточность, он на удивление прост. Он не использует никаких нейронных сетей, случайных лесов или чего-то другого, похожего на машинное обучение. Если разобраться с идеей, он станет для вас очень понятным и интуитивным.

Большинство реализаций и объяснений коллапса волновой функции — это полная, оптимизированная по скорости версия алгоритма. Разумеется, все они важны и необходимы, но в них сложно разобраться с нуля. В этом посте я буду объяснять всё понятным я простым языком, сосредоточившись на версии Wavefunction с ограничениями, которую я назвал Even Simpler Tiled Model. Кроме того, я выложил пример реализации ESTM на Github. Код в нём неэффективный и медленный, но очень хорошо читаемый и подробно прокомментирован. Как только вы разберётесь в технологии, лежащей в основе ESTM, то станете ближе к пониманию более сложных версий алгоритма. Если хотите понять алгоритм коллапса волновой функции, то эта статья будет хорошим началом.

Давайте начнём с истории.

Свадьба

Представьте, что вы планируете свою свадьбу. Кроме подбора украшений и музыки вам нужно создать план рассаживания гостей для обеда. Ваша семья любит поспорить и капризничать, поэтому это может оказаться сложным. Отец не может сидеть ближе чем в двух столах от матери. Двоюродной сестре становится одиноко, если она не сидит с другой двоюродной сестрой. А дядю Роя лучше не сажать рядом с экологически настроенными членами семьи вашего партнёра. Осталось всего 5 часов до прибытия еды, поэтому вы решаете атаковать эту упрямую задачу при помощи алгоритма коллапса волновой функции.

Вы начинаете с длинного списка правил и пустого плана рассаживания гостей.


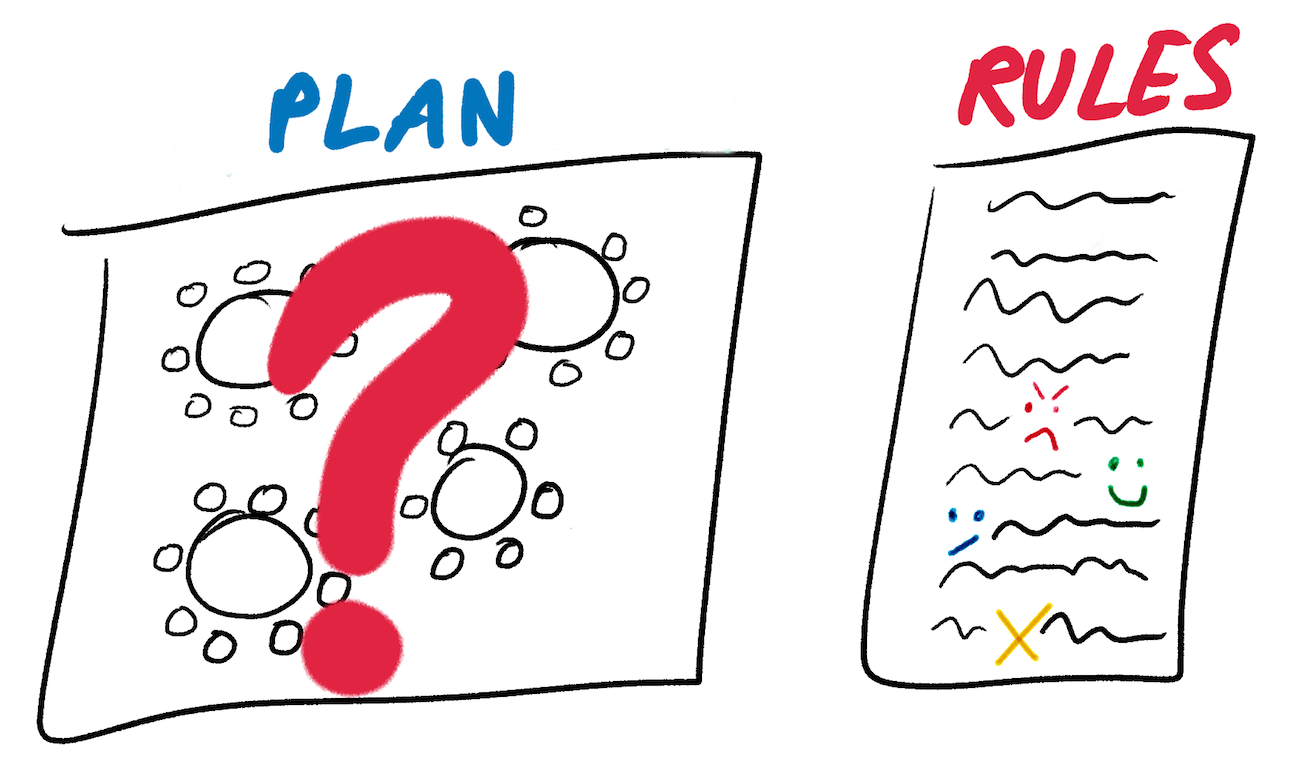
Вы создаёте исходную волновую функцию плана. Она привязывает каждый стул к списку людей, которые на нём могут сидеть. Пока на любой стул может сесть любой человек. Волновая функция рассаживания гостей начинается с полной суперпозиции (понятие заимствовано из квантовой физики) каждой возможной схемы.


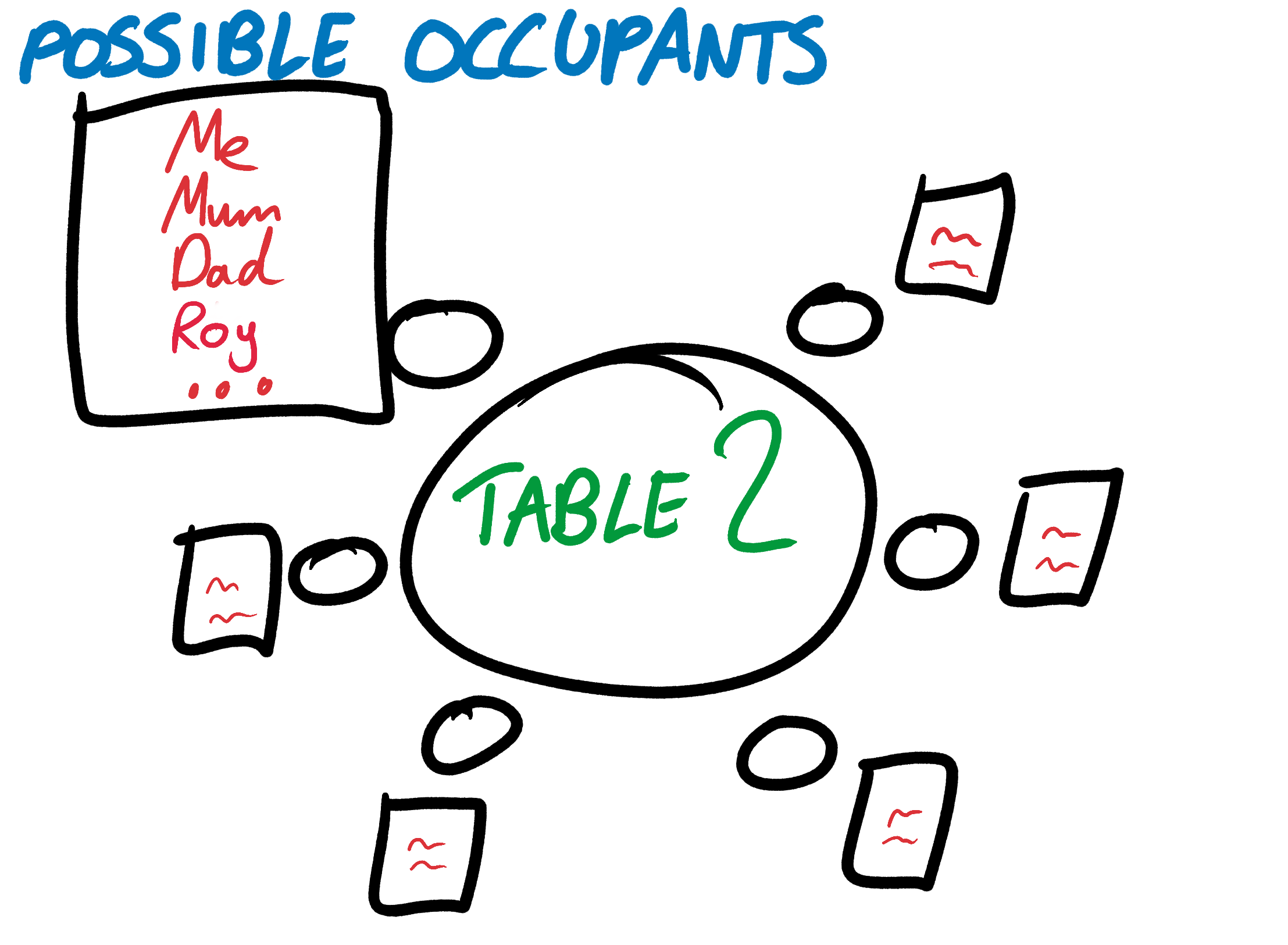
Кот Шрёдингера был одновременно мёртвым и живым, пока кто-нибудь не откроет ящик и не проверит; ваш план одновременно является каждой возможной схемой, пока вы не наведёте в нём порядок. Полная суперпозиция — полезная теоретическая конструкция, но она не поможет вашей бабушке разобраться, где ей нужно сидеть. Вам нужно привести волновую функцию расположения гостей к единственному определённому состоянию, которую потом можно превратить в обычные, неквантовые карточки с именами.

Начинаем мы это делать, выполняя коллапс волновой функции для одного стула. Выбираем стул, смотрим на список людей, которые могут на нём сидеть, и случайным образом назначаем его одному из них. При этом волновая функция стула становится коллапсированной.


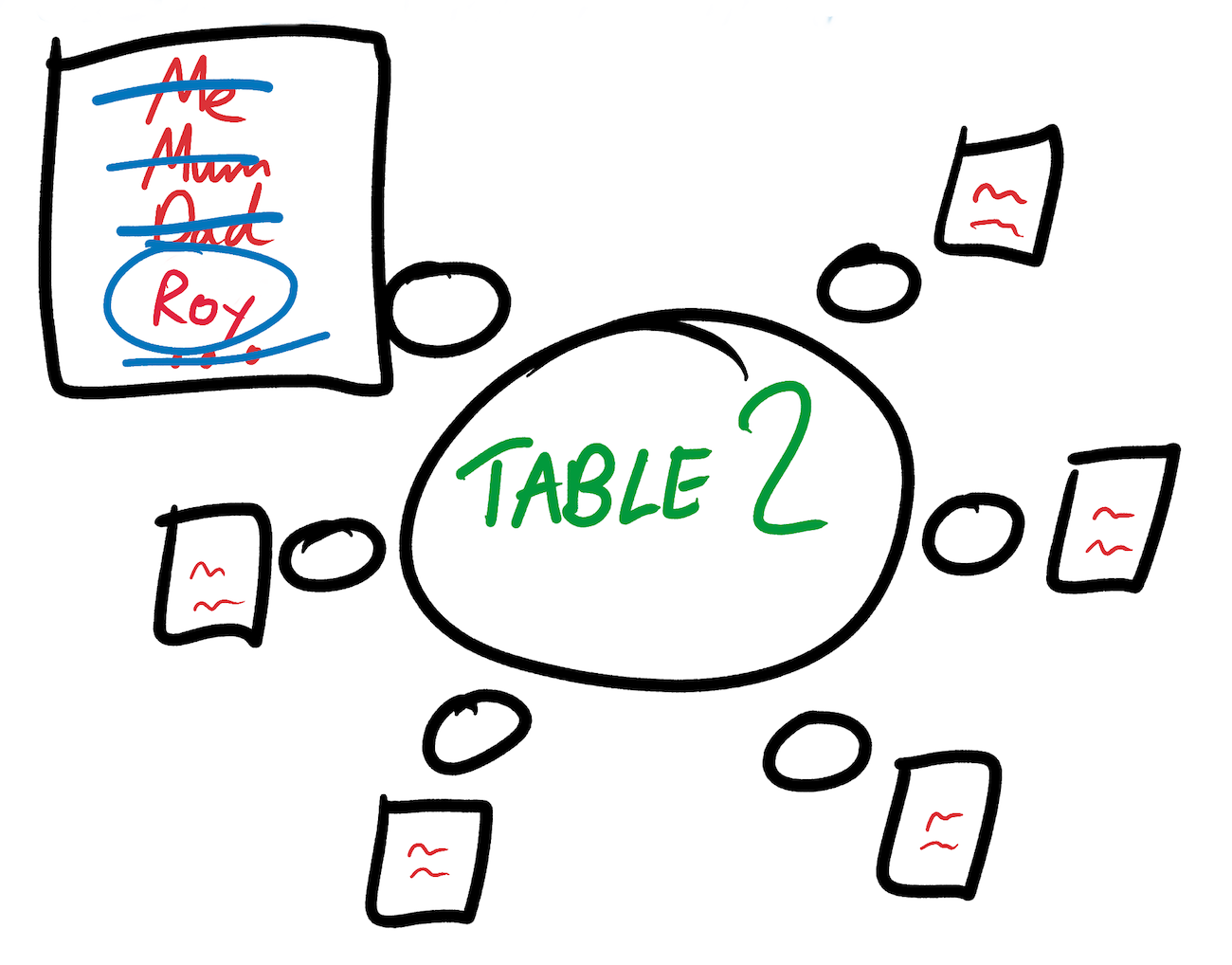
Этот выбор имеет последствия, распространяющиеся на волновые функции остальных стульев. Если дядя Рой будет сидеть за столом 2, то кузен Фрэнк и Мишель Обама (друг семьи вашего партнёра) точно не будут рядом с ним. А если Мишель не сядет за стол 2, то Барака за ним тоже не будет. Мы обновляем волновую функцию плана расположения, вычёркивая людей из списков возможных кандидатов.


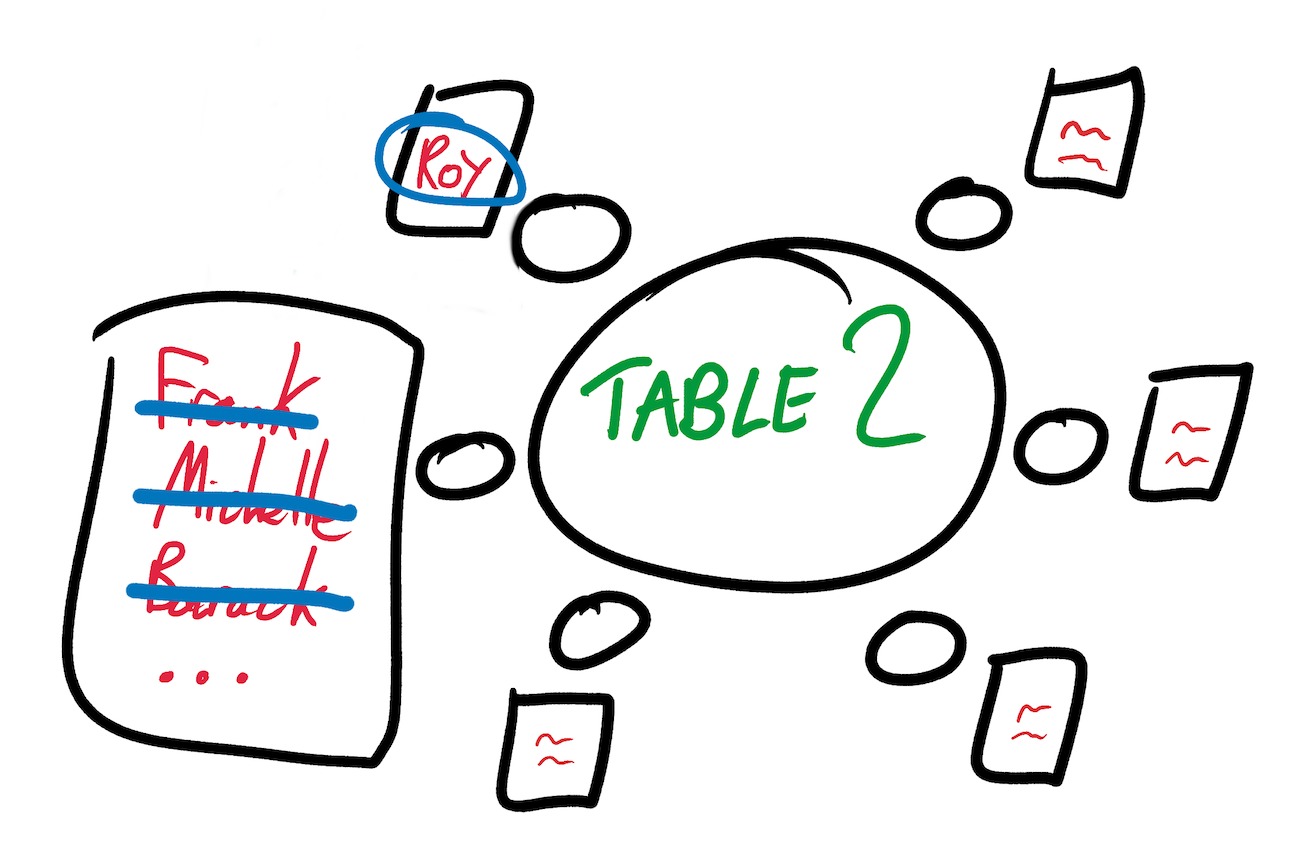
Как только колебания устоятся, мы повторяем этот процесс. Выбираем ещё один стул с несколькими возможными кандидатами и коллапсируем его волновую функцию, случайным образом выбирая одного из допустимых для него людей. Снова распространяем колебания, вызванные этим выбором, на весь остальной план, удаляя из волновой функции стула людей, если они больше не могут на нём сидеть.

Мы повторяем этот процесс или пока волновая функция не коллапсирует (то есть в ней не останется ровно 1 сидящий человек), или пока мы не достигнем противоречия. Противоречие — это стул, на котором не может сидеть никто, потому что всех их исключили из-за предыдущих выборов. Противоречие делает невозможность коллапс всей волновой функции.

Если вы достигли противоречия, то проще всего будет начать сначала. Отбросить всю предыдущую работу, найти новый пустой план и запустить алгоритм заново, выполнив коллапс волновой функции для другого случайного стула. Можно также реализовать систему возврата назад, позволяющую отменять отдельный выбор, а не отказываться сразу от всего («что если пересадить Шейлу на стул 54?»).

После нескольких фальстартов вы наконец достигнете полностью коллапсированного состояния, в котором каждый стул назначен ровно одному человеку и соблюдены все правила. Готово!

От свадьбы к битовым картам

Это не теоретический пример. Вы действительно можете реализовать вариант коллапса волновой функции, который будет создавать план рассаживания гостей для свадьбы. Однако в более традиционном Wavefunction Collapse мы обычно пытаемся не рассадить людей на свадьбе, а расставить пиксели на выходящем изображении. Тем не менее, процесс будет очень похожим. Мы обучаем алгоритм набору правил, которым должны удовлетворять выходные данные. Инициализируем волновую функцию. Выполняем коллапс одного элемента и распространяем последствия на остальную часть волновой функции. И продолжаем так делать, или пока волновая функция полностью не коллапсирует, или пока мы не достигнем противоречия.

Традиционный коллапс волновой функции отличается от свадебного коллапса тем, как мы обучаем алгоритм правилам, которые он должен соблюдать. В свадебной версии нам пришлось записывать правила самостоятельно. Но в традиционной версии мы просто даём алгоритму изображение-пример, и исходя из него алгоритм создаёт всё остальное. Он парсит пример, анализирует его паттерны и выясняет, как должны выстраиваться пиксели или тайлы.

Давайте начнём исследование реального коллапса волновой функции с рассмотрения простого особого случая, который ExUtumno (создатель алгоритма) называет простой тайловой моделью (Simple Tiled Model).

Simple Tiled Model

В модели Simple Tiled Model входящие и выходящие изображения строятся из небольшого количества заранее определённых тайлов, и каждый квадрат в выходящем изображении ограничивается только его четырьмя ближайшими соседями. Например, предположим, что мы генерируем случайные миры для двухмерной игры с видом сверху. У нас могут быть тайлы для суши, побережья и моря, а также набор правил вида «побережье может находиться рядом с морем», «суша может быть рядом с побережьем» и «море может быть рядом с другим морем».


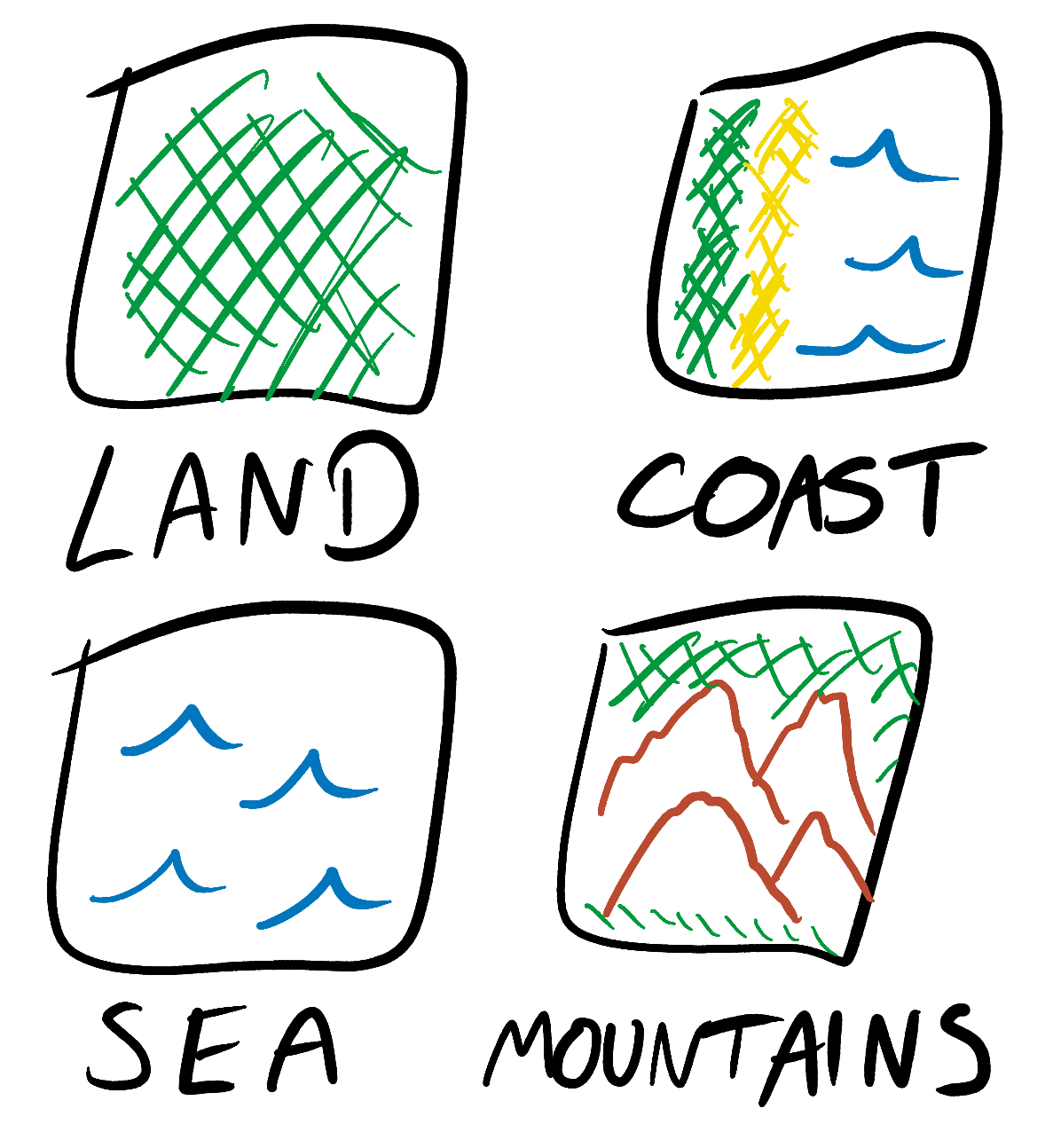
Simple Tiled Model учитывает симметрию и поворот своих тайлов. Например, суша может находиться рядом с побережьем, но только в правильной ориентации.


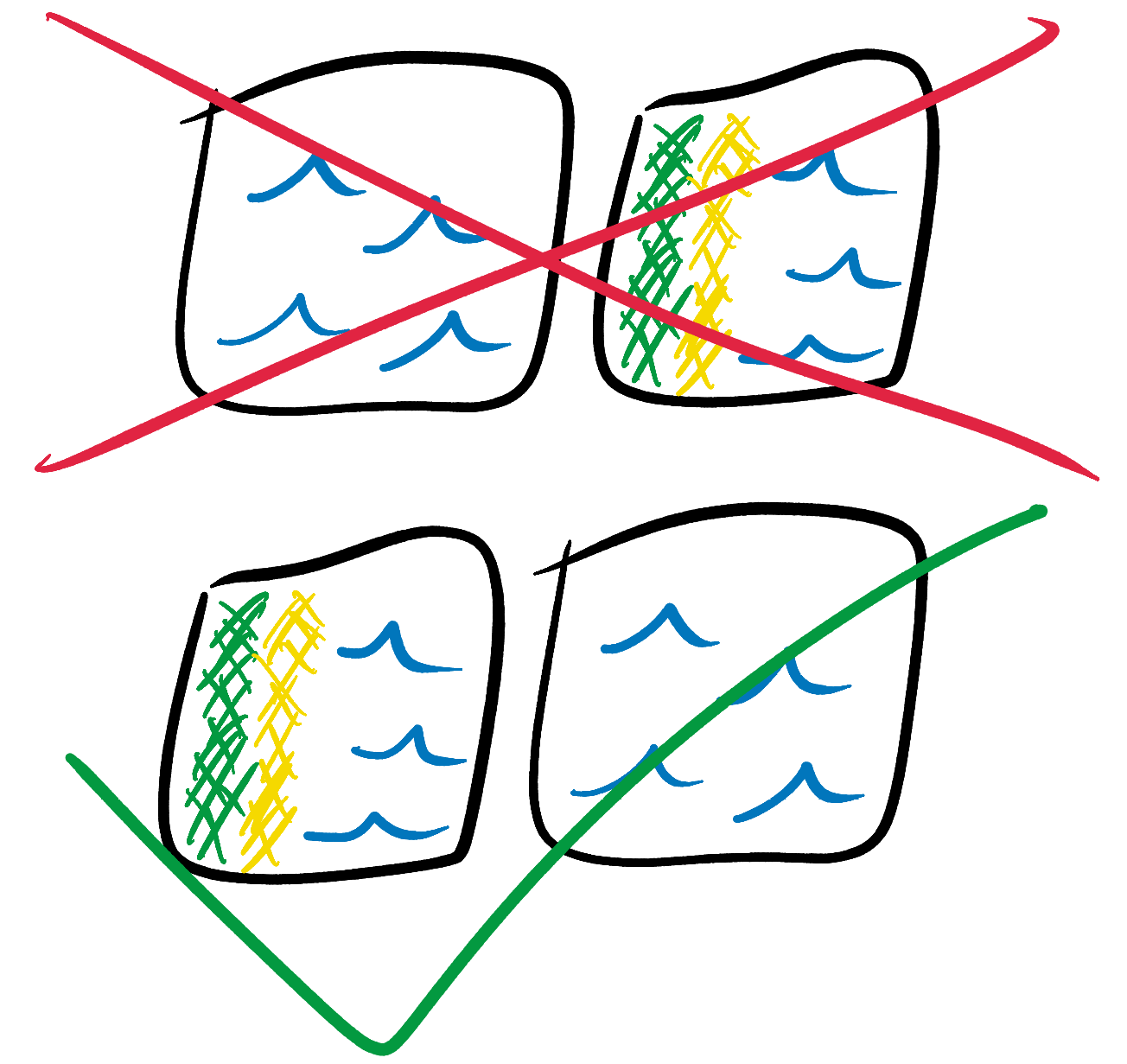
Эта обработка симметрии обеспечивает более качественные выходные изображения, но усложняет код. Чтобы не усложнять, давайте рассмотрим ещё более простой вид коллапса волновой функции, который я назвал Even Simpler Tiled Model.

Even Simpler Tiled Model

Even Simpler Tiled Model («ещё более простая тайловая модель») похожа на Simple Tiled Model, но её тайлы не имеют свойств симметрии. Каждый тайл — это один пиксель одного цвета, то есть мы никак не сможем перепутать их края.


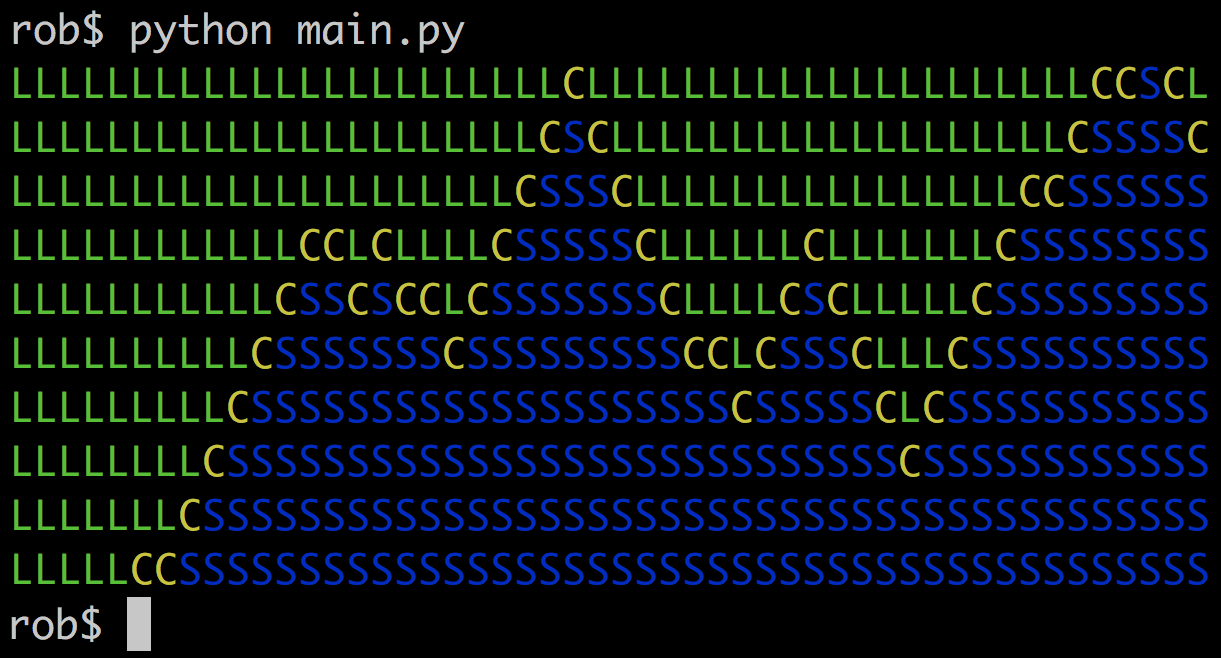
Правила Even Simpler Tiled Model определяют, какие тайлы можно размещать рядом друг с другом и в какой ориентации. Каждое правило представляет собой кортеж из трёх элементов (3-tuple): двух тайлов и направления. Например, (SEA, COAST, LEFT) означает, что тайл SEA (море) может размещаться СЛЕВА от тайла COAST (побережье). Это правило должно сопровождаться другим правилом, описывающим ситуацию с точки зрения COAST — (COAST, SEA, RIGHT).


Если вы хотите, чтобы тайлы SEA могли располагаться не только СЛЕВА, но и СПРАВА от тайлов COAST. то им нужны дополнительные правила: (SEA, COAST, RIGHT) и (COAST, SEA, LEFT).

Как я сказал выше, нам не нужно создавать список всех этих правил самостоятельно. Коллапс волновой функции может создать набор правил для Even Simpler Tile Model парсингом изображения-примера и собиранием списка всех 3-tuple, которые в нём содержатся.


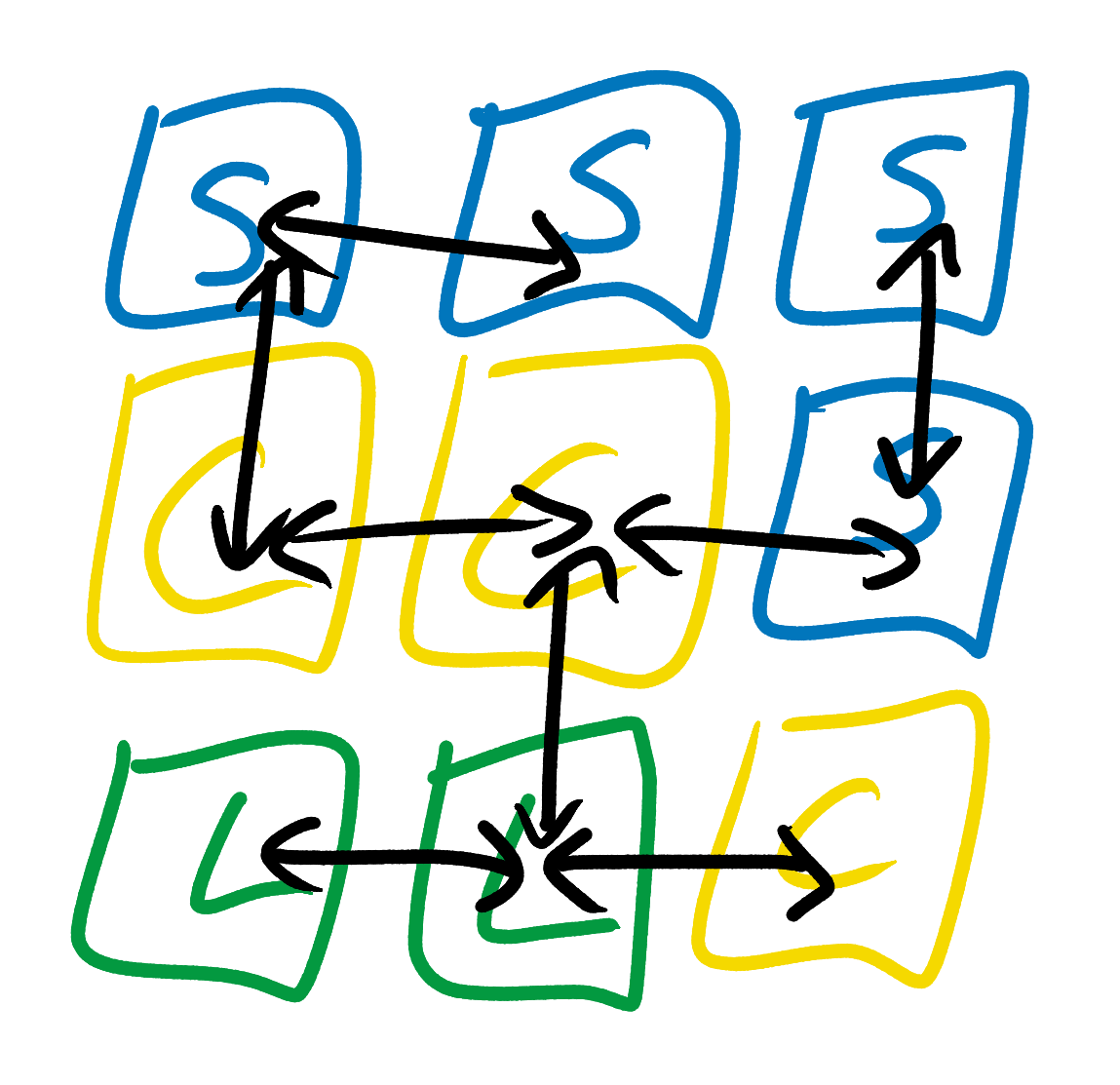
Исследовав показанный выше пример изображения, Even Simpler Tiled Model замечает, что тайлы моря могут быть только под или сбоку от тайлов побережья, или в любом месте рядом с другими тайлами моря. Также она замечает, что тайлы побережья могут располагаться рядом с сушей, морем или другими тайлами побережья, но только над тайлами моря и под тайлами суши. Она не пытается вывести никакие более сложные правила, например «тайлы моря должны быть рядом по крайней мере с одним тайлом моря» или «каждый остров должен содержать как минимум один тайл суши». Ни один из тайлов не может влиять на то, что какие-то типы тайлов могут или не могут располагаться в двух или более квадратах от них. Это похоже на модель плана свадьбы, в которой единственное правило: «X может сидеть рядом с Y».

При анализе входящего изображения нам также нужно записывать частоту, с которой встречается каждый из тайлов. Позже мы используем эти числа как веса при выборе волновой функции квадрата, коллапс которой нужно выполнить, а также при выборе тайла, назначаемого квадрату при его коллапсировании.

Узнав правила, которых должно придерживаться выходящее изображение, мы готовы к построению коллапсированию волновой функции выходящего изображения.

Коллапс

Как и в примере со свадьбой, мы начинаем процесс коллапсированя с волновой функции, в которой каждый квадрат выходящего изображения находится в суперпозиции каждого типа тайла.


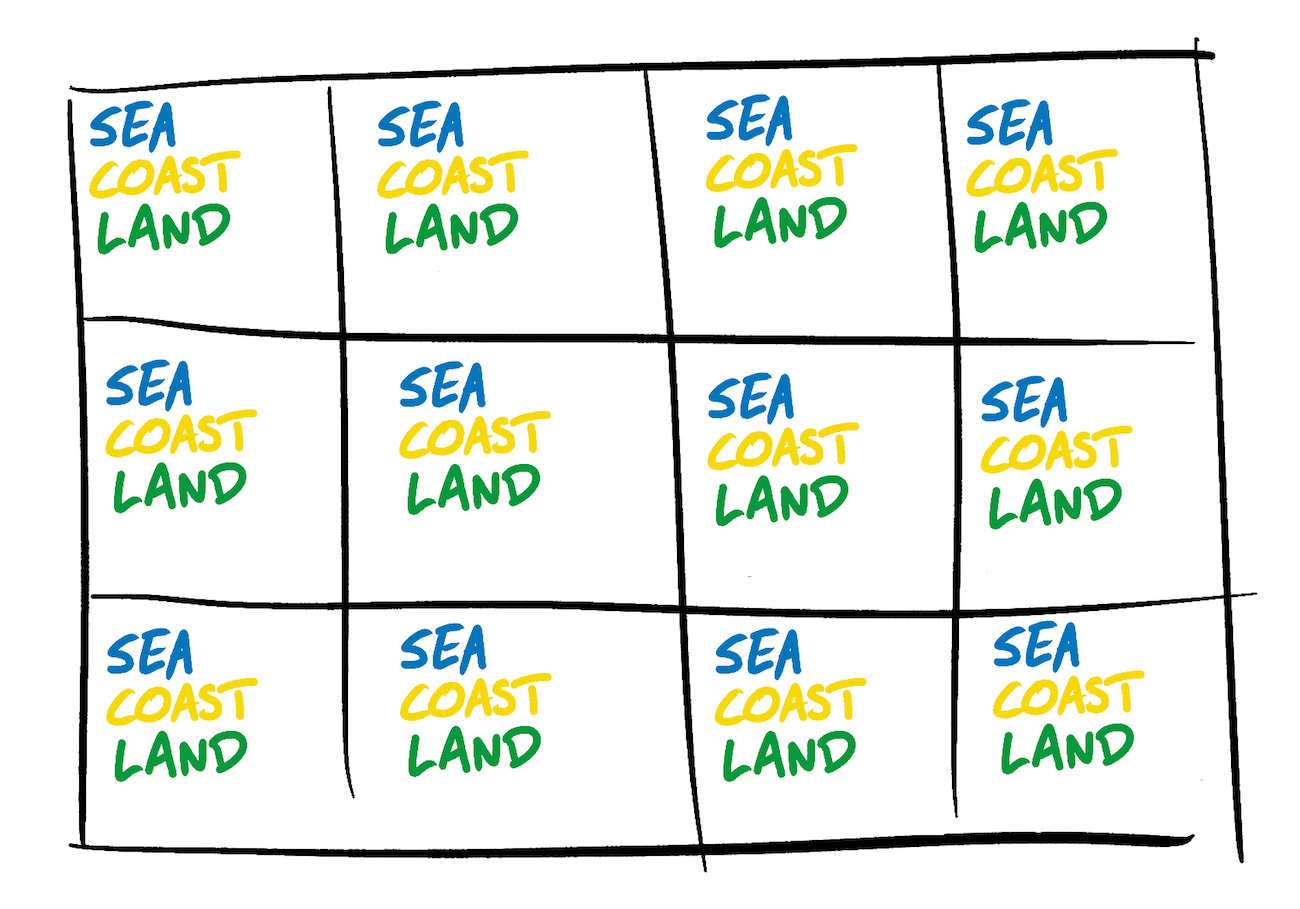
Начнём с выбора квадрата, волновую функцию которого будем коллапсировать. В примере со свадьбой этот выбор делался случайно. Однако, как заметил ExUtumno, люди обычно подходят к таким задачам иначе. Вместо этого они ищут квадраты с наименьшей энтропией. Энтропия — это мера неопределённости и беспорядка. В общем случае квадрат с высокой энтропией — это квадрат со множеством возможных тайлов, оставшихся в его волновой функции. Пока очень непонятно, к какому тайлу он в конечном итоге коллапсирует. Квадрат с низкой энтропией — это квадрат с малым количеством возможных тайлов в волновой функции. Набор тайлов, к одному из которых он в результате коллапсирует, уже очень ограничен.

Например, в модели Even Simpler Tile Model квадрат без информации об окружающих его квадратах ничем не ограничен и может стать любым тайлом. Следовательно, он имеет очень высокую энтропию. Но квадрат, вокруг которого уже коллапсировало несколько квадратов, может иметь на выбор всего 2 тайла.


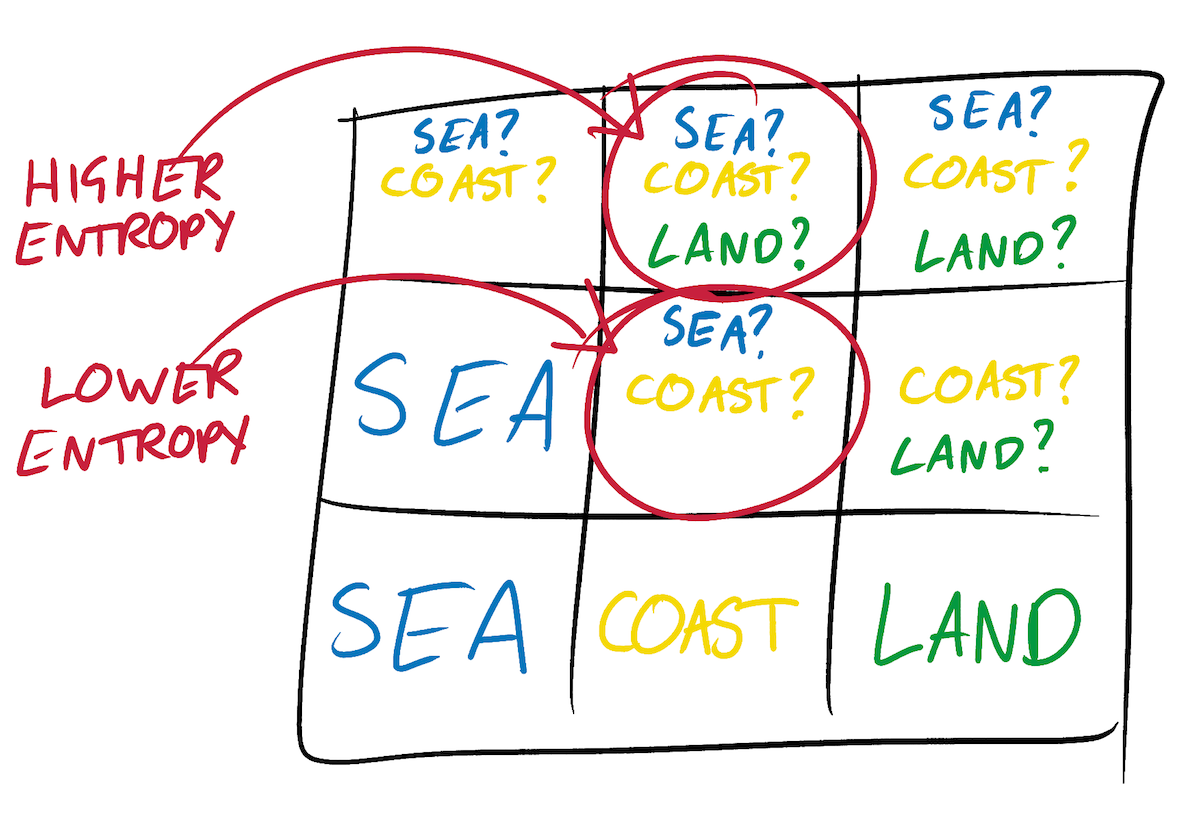
Волновая функция центрального квадрата на рисунке выше не полностью коллапсировала, но мы уже знаем, что она не может быть тайлом суши. Тем не менее, она уже ограничена, а значит, имеет энтропию ниже, чем у правого верхнего квадрата, который всё ещё может быть сушей, морем или побережьем.

Именно на такие ограниченные тайлы с низкой энтропией обычно и обращают внимание люди, когда вручную решают подобные задачи. Даже если вы не пользуетесь коллапсом волновой функции для создания плана размещения гостей на свадьбе и будете составлять его самостоятельно, то всё равно сосредоточитесь на тех областях плана, в которых уже есть наибольшее количество ограничений. Вы не будете сажать Дуэйна за стол 1, а затем случайным образом перепрыгивать, чтобы посадить Кэти за стол 7 (который пока пуст). Вы сначала посадите Дуэйна, потом разберётесь, кто может сидеть рядом с ним, затем кто может сидеть рядом с этим человеком, и так далее. Я пока не видел обоснований этого, но моя интуиция говорит, что при использовании этой эвристики минимальной энтропии скорее всего будет получаться меньше противоречий, чем при случайном выборе квадратов для коллапсирования.

В качестве формулы энтропии в алгоритме коллапса волновой функции применяется формула Шеннона. В ней используются веса тайлов, которые мы спарсили из входящего изображения на предыдущем этапе:

# Sums are over the weights of each remaining
# allowed tile type for the square whose
# entropy we are calculating.
shannon_entropy_for_square =
  log(sum(weight)) -
  (sum(weight * log(weight)) / sum(weight))

Вычислив квадрат волновой функции с наименьшей энтропией, мы коллапсируем её волновую функцию. Мы делаем это, случайным образом выбирая один из тайлов, пока ещё доступных для квадрата, взвешенный на веса тайлов, которые мы спарсили из входящего изображения. Веса используются потому, что это обеспечивает более реалистичное изображение на выходе. Допустим, волновая функция квадрата сообщает, что он может быть сушей или побережьем. Мы не всегда должны выбирать один из вариантов с вероятностью 50%. Если во входящем изображении больше тайлов суши, чем побережья, то нам стоит отразить этот перевес и в выходном изображении. Реализуется это при помощи простых глобальных весов. Если в примере изображения есть 20 тайлов суши и 10 тайлов побережья, то квадрат коллапсирует в сушу с вероятностью 2/3, а в побережье — с оставшейся вероятностью 1/3.

Затем мы распространяем последствия выбора на остальную волновую функцию выходных данных («если тот тайл оказался морем, то этот не может быть сушей, то есть этот не может быть побережьем»). Когда все эти сотрясения улягутся, мы повторяем процесс, используя эвристику минимальной энтропии для выбора следующего коллапсирующего тайла. Повторяем этот цикл коллапсирования-распространения, или пока вся волновая функция выходного изображения полностью не коллапсирует и мы сможем вернуть результат, или пока мы не достигнем противоречения и вернём ошибку.

В итоге мы создали мир (или ошибку).

Куда двигаться дальше

Разобравшись с моделью Even Simpler Tiled Model, вы готовы подниматься выше по лестнице мощности и сложности алгоритма. Начните с Simple Tiled Model, которую мы упоминали в начале этого поста, затем перейдите к полной Overlapping Model. В Overlapping Model тайлы или пиксели влияют друг на друга издалека. Если вы понимаете в таких вещах, то ExUtumno замечает, что Simple Tiled Model схожа с цепью Маркова порядка-1, а более сложные модели напоминают цепи большего порядка.

Wavefunction Collapse даже может учитывать дополнительные ограничения, например «этот тайл должен быть морем» или «этот пиксель должен быть красным» или «в выходных данных может быть только один монстр». Обо всё этом рассказывается README основного проекта. Также можно изучить оптимизации скорости, внесённые в полную реализацию. Необязательно повторно вычислять энторпию каждого квадрата в каждой итерации, а распространение информации по волновой функции можно сделать значительно быстрее. Эти аспекты становятся важнее при увеличении размеров выходящих изображений.

Коллапс волновой функции — это красивый и мощный инструмент, который стоит освоить. Вспомните об этом, когда в следующий раз будете планировать свадьбу или генерировать процедурный мир.