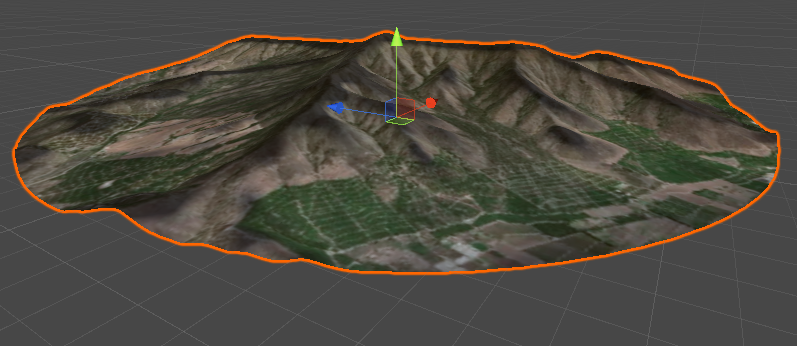
Этот туториал посвящён интерактивным картам и их созданию в Unity при помощи шейдеров.
Этот эффект может служить основой более сложных техник, например голографических проекций или даже песочного стола из фильма «Чёрная пантера».
Источником вдохновения для этого туториала стал опубликованный Baran Kahyaoglu твит, демонстрирующий пример того, что он создаёт для Mapbox.
Сцена (за исключением карты) взята из демо Unity Visual Effect Graph Spaceship (см. ниже), которое можно скачать здесь.
Часть 1. Смещение вершин
Анатомия эффекта
Первое, что можно сразу заметить — географические карты плоски: если их использовать в качестве текстур, то им не хватает трёхмерности, которую бы имела настоящая 3D-модель соответствующей области карты.
Можно применить такое решение: создать 3D-модель той области, которая нужна в игре, а затем наложить на неё текстуру из географической карты. Это поможет решить задачу, но требует много времени и не позволит реализовать эффект «прокрутки» из видео Baran Kahyaoglu.
Очевидно, что лучше всего применить более технический подход. К счастью, для изменения геометрии 3D-модели можно использовать шейдеры. С их помощью можно превратить любую плоскость в долины и горы нужной нам области.
В этом туториале мы используем карту коммуны Кильота в Чили, знаменитой своими характерными холмами. На изображении ниже показана текстура области, нанесённая на круглый меш.
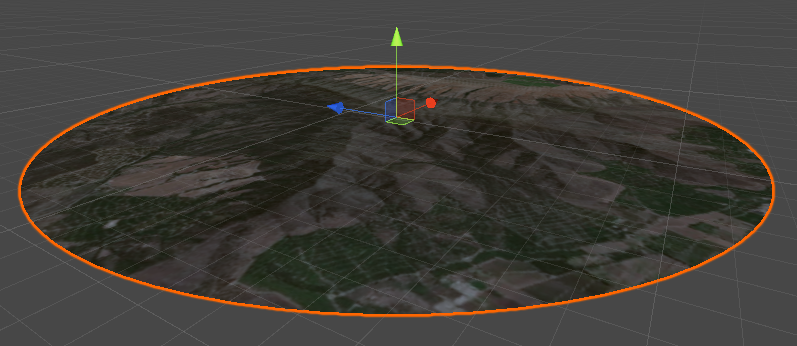
Хоть мы и видим холмы и горы, они всё-таки совершенно плоские. Это разрушает иллюзию реализма.
Экструдирование нормалей
Первым шагом к использованию шейдеров для изменения геометрии является техника под названием «экструдирование нормалей» (normal extrusion). Ей требуется модификатор вершин: функция, способная манипулировать отдельными вершинами 3D-модели.
Способ применения модификатора вершин зависит от типа используемого шейдера. В этом туториале мы будем изменять Surface Standard Shader — один из типов шейдеров, которые можно создавать в Unity.
Существует множество способов манипуляции вершинами 3D-модели. Один из самых первых способов, описываемых в большинстве туториалов по вершинным шейдерам — это экструдирование нормалей. Он заключается в выталкивании каждой вершины «наружу» (экструдировании), что придаёт 3D-модели более раздутый вид. «Наружу» обозначает, что каждая вершина движется вдоль направления нормали.
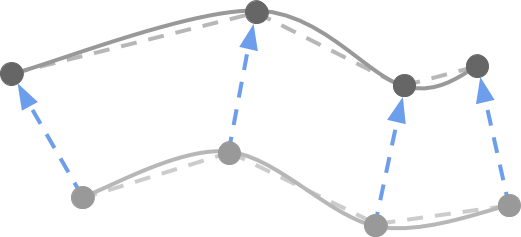
Для гладких поверхностей это срабатывает очень хорошо, но в моделях с плохим соединением вершин такой способ может создавать странные артефакты. Этот эффект хорошо объяснён в одном из моих первых туториалов: A Gentle Introduction to Shaders, где я показал, как экструдировать и интрудировать 3D-модель.

Добавить экструдирование нормалей в поверхностный шейдер очень легко. У каждого поверхностного шейдера есть директива
#pragma, которая используется для передачи дополнительной информации и команд. Одной из таких команд является vert, которая обозначает, что для обработки каждой вершины 3D-модели будет использоваться функция vert.Отредактированный шейдер выглядит следующим образом:
#pragma surface surf Standard fullforwardshadows addshadow vertex:vert
...
float _Amount;
...
void vert(inout appdata_base v)
{
v.vertex.xyz += v.normal * _Amount;
}Так как мы изменяем позицию вершин, нам также нужно использовать
addshadow, если мы хотим, чтобы модель правильно отбрасывала тени на саму себя.Что такое appdata_base?
Как видите, мы добавили функцию модификатора вершин (
В некоторых случаях этого недостаточно и нам могут потребоваться другие свойства, например цвет вершины (
vert), которая принимает в качестве параметра структуру под названием appdata_base. Эта структура хранит информацию о каждой отдельной вершине 3D-модели. Она содержит не только позицию вершины (v.vertex), но и другие поля, например направление нормали (v.normal) и связанную с вершиной информацию о текстуре (v.texcoord).В некоторых случаях этого недостаточно и нам могут потребоваться другие свойства, например цвет вершины (
v.color) и направление касательной (v.tangent). Модификаторы вершин могут задаваться при помощи множества других входящих структур, в том числе appdata_tan и appdata_full, которые предоставляют больше информации ценой малых затрат производительности. Подробнее о appdata (и её вариантах) можно прочитать в Unity3D wiki.Как возвращаются значения из vert?
Вершинная функция не имеет возвращаемого значения. Если вы знакомы с языком C#, то должны знать, что структуры передаются по значению, то есть при изменении
Однако
v.vertex это влияет только на копию v, область видимости которой ограничена телом функции.Однако
v также объявляется как inout, и это значит, что она используется и для ввода, и для вывода. Любые вносимые изменения изменяют саму переменную, которую мы передаём в vert. Ключевые слова inout и out очень часто используются в компьютерной графике, и их примерно можно соотнести с ref и out в C#.Экструдирование нормалей с текстурами
Использованный нами выше код работает правильно, но он далёк от того эффекта, которого мы хотим достичь. Причина заключается в том, что мы не хотим экструдировать все вершины на одинаковую величину. Мы хотим, чтобы поверхность 3D-модели соответствовала долинам и горам соответствующего географического региона. Сначала нам каким-то образом нужно хранить и извлекать информацию о том, насколько поднята каждая точка карты. Мы хотим, чтобы на экструдирование влияла текстура, в которой закодированы высоты ландшафта. Такие текстуры часто называют картами вершин (heightmaps), однако нередко они также называются картами глубин (depthmaps), в зависимости от контекста. Получив информацию о высотах, мы сможем модифицировать экструдирование плоскости на основании карты высот. Как показано на схеме, это позволит нам контролировать поднятием и опусканием областей.

Довольно просто найти спутниковое изображение интересующей вас географической области и связанную с ней карту высот. Ниже показана спутниковая карта Марса (сверху) и карта высот (снизу), которые использовались в этом туториале:


Я подробно рассказывал о концепции карты глубин в ещё одной серии туториалов под названием «3D-фотографии Facebook изнутри: шейдеры параллакса» [перевод на Хабре].
В этом туториале мы будем считать, что карта высот хранится как изображение в градациях серого, где чёрный и белый цвет соответствуют меньшим и большим высотам. Также нам нужно, чтобы эти значения масштабировались линейно, то есть разность цветов, например в
0.1 соответствовала разности высот между 0 и 0.1 или между 0.9 и 1.0. Для карт глубин это не всегда верно, потому что многие из них хранят информацию о глубине в логарифмическом масштабе.Для сэмплирования текстуры необходимы два элемента информации: сама текстура и UV-координаты точки, которую мы хотим сэмплировать. К последним можно получить доступ через поле
texcoord, хранящееся в структуре appdata_base. Это UV-координата, связанная с текущей обрабатываемой вершиной. Сэмплирование текстур в поверхностной функции выполняется при помощи tex2D, однако когда мы находимся в вершинной функции, требуется tex2Dlod.В показанном ниже фрагменте кода текстура под названием
_HeightMap используется для модификации величины экструдирования, выполняемого для каждой вершины:sampler2D _HeightMap;
...
void vert(inout appdata_base v)
{
fixed height = tex2Dlod(_HeightMap, float4(v.texcoord.xy, 0, 0)).r;
vertex.xyz += v.normal * height * _Amount;
}Почему в качестве вершинной функции нельзя использовать tex2D?
Если взглянуть на код, который Unity генерирует для Standard Surface Shader, то можно заметить, что он уже содержит пример того, как сэмплировать текстуры. В частности, он сэмплирует основную текстуру (под названием
_MainTex) в поверхностной функции (под названием surf) при помощи встроенной функции tex2D.И в самом деле,
tex2D используется для сэмплирования пикселей из текстуры, вне зависимости от того, что в ней хранится, цвета или высоты. Однако можно заметить, что tex2D невозможно использовать в вершинной функции.Причина в том, что
tex2D не только считывает пиксели из текстуры. Она также решает, какую версию текстур использовать, в зависимости от расстояния до камеры. Эта техника называется MIP-текстурированием (mipmapping): она позволяет иметь уменьшенные версии одной текстуры, которые можно автоматически использовать на различных расстояниях.В поверхностной функции шейдер уже знает, какую MIP-текстуру использовать. Эта информация может быть ещё не доступна в вершинной функции, и поэтому
tex2D нельзя использовать с полной уверенностью. В отличие от неё, функции tex2Dlod можно передать два дополнительных параметра, которые в этом туториале могут иметь нулевое значение.Результат чётко заметен на изображениях ниже

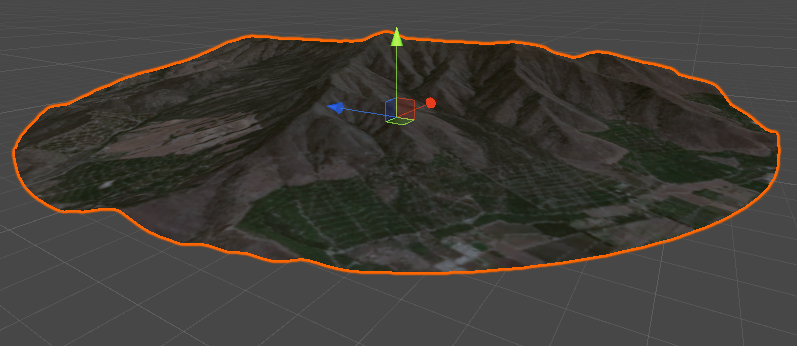
В данном случае можно выполнить одно небольшое упрощение. Код, который мы рассматривали ранее, может работать с любой геометрией. Однако мы можем допустить, что поверхность абсолютно плоская. На самом деле мы действительно хотим применить этот эффект к плоскости.
Следовательно, можно удалить
v.normal и заменить её на float3(0, 1, 0):void vert(inout appdata_base v)
{
float3 normal = float3(0, 1, 0);
fixed height = tex2Dlod(_HeightMap, float4(v.texcoord.xy, 0, 0)).r;
vertex.xyz += normal * height * _Amount;
}Мы могли это сделать, потому что все координаты в
appdata_base хранятся в пространстве модели, то есть они задаются относительно центра и ориентации 3D-модели. Перенос, поворот и масштабирование при помощи transform в Unity меняют позицию, поворот и масштаб объекта, но не влияют на исходную 3D-модель.Часть 2. Эффект прокрутки
Всё, что мы сделали выше, довольно неплохо работает. Прежде чем продолжить, вынесем код, необходимый для вычисления новой высоты вершины, в отдельную функцию
getVertex:float4 getVertex(float4 vertex, float2 texcoord)
{
float3 normal = float3(0, 1, 0);
fixed height = tex2Dlod(_HeightMap, float4(texcoord, 0, 0)).r;
vertex.xyz += normal * height * _Amount;
return vertex;
}Тогда вся функция
vert будет иметь вид:void vert(inout appdata_base v)
{
vertex = getVertex(v.vertex, v.texcoord.xy);
}Мы сделали так потому, что в ниже нам понадобится вычислять высоту нескольких точек. Благодаря тому, что эта функциональность будет в собственной отдельной функции, код станет намного проще.
Вычисление UV-координат
Однако это приводит нас к другой проблеме. Функция
getVertex зависит не только от позиции текущей вершины (v.vertex), но и от её UV-координат (v.texcoord).Когда мы хотим вычислить смещение высоты вершины, которую в данный момент обрабатывает функция
vert, оба элемента данных доступны в структуре appdata_base. Однако что произойдёт, если нам нужно сэмплировать позицию соседней точки? В этом случае мы можем знать позицию xyz в пространстве модели, но не имеем доступа к её UV-координатам.Это означает, что имеющаяся система способна вычислять смещение высоты только для текущей вершины. Такое ограничение не позволит нам двигаться дальше, поэтому нужно найти решение.
Проще всего будет найти способ вычисления UV-координат 3D-объекта, зная позицию его вершины. Это очень сложная задача, и существует несколько техник её решения (одна из самых популярных — это трипланарная проекция). Но в данном конкретном случае нам не нужно сопоставлять UV с геометрией. Если мы допустим, что шейдер всегда будет применяться к плоскому мешу, то задача становится тривиальной.
Мы можем вычислять UV-координаты (нижнее изображение) из позиций вершин (верхнее изображение) благодаря тому, что на плоском меше и те, и другие накладываются линейно.

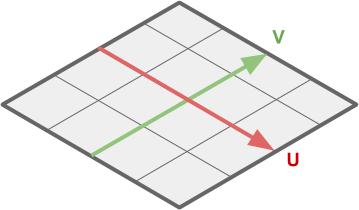
Это значит, что для решения нашей задачи нам нужно преобразовать компоненты XZ позиции вершины в соответствующие UV-координаты.
Такая процедура называется линейной интерполяцией. Она подробно рассмотрена на моём веб-сайте (например: The Secrets Of Colour Interpolation).
В большинстве случаев значения UV находятся в интервале от до ; координаты каждой вершины, напротив, потенциально ничем не ограничены. С точки зрения математики, для преобразования из XZ в UV нам нужны только их предельные значения:
- ,
- ,
- ,
- ,
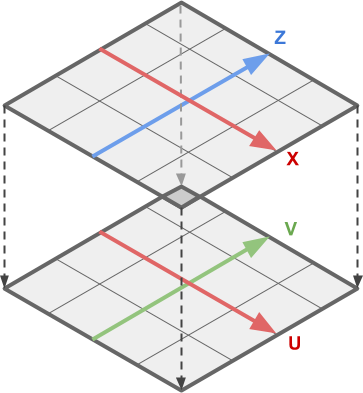
которые показаны ниже:

Эти значения изменяются в зависимости от используемого меша. На плоскости Unity UV-координаты находятся в интервале от до , а координаты вершин находятся в интервале от до .
Уравнения преобразования XZ в UV имеют вид:
(1)
Как они выводятся?
Если вам незнакомо понятие линейной интерполяции, то эти уравнения могут показаться довольно пугающими.
Однако выводятся они достаточно просто. Давайте рассмотрим только пример . У нас есть два интервала: один имеет значения от до , другой — от до . Входящими данными для координаты является координата текущей обрабатываемой вершины, а выходными данными будет координата , используемая для сэмплирования текстуры.
Нам необходимо сохранить свойства пропорциональности между и его интервалом, и и его интервалом. Например, если имеет значение 25% от его интервала, то тоже будет иметь значение 25% от его интервала.
Всё это показано на следующей схеме:

Из этого мы можем вывести, что пропорция, составляемая красным отрезком по отношению к розовому, должна быть такой же, что и пропорция между синим отрезком и голубым:
(2)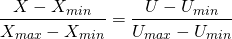
Теперь мы можем преобразовать показанное выше уравнение, чтобы получить :

и это уравнение имеет точно такой же вид, что и показанное выше (1).
Однако выводятся они достаточно просто. Давайте рассмотрим только пример . У нас есть два интервала: один имеет значения от до , другой — от до . Входящими данными для координаты является координата текущей обрабатываемой вершины, а выходными данными будет координата , используемая для сэмплирования текстуры.
Нам необходимо сохранить свойства пропорциональности между и его интервалом, и и его интервалом. Например, если имеет значение 25% от его интервала, то тоже будет иметь значение 25% от его интервала.
Всё это показано на следующей схеме:

Из этого мы можем вывести, что пропорция, составляемая красным отрезком по отношению к розовому, должна быть такой же, что и пропорция между синим отрезком и голубым:
(2)
Теперь мы можем преобразовать показанное выше уравнение, чтобы получить :

и это уравнение имеет точно такой же вид, что и показанное выше (1).
Эти уравнения можно реализовать в коде следующим образом:
float2 _VertexMin;
float2 _VertexMax;
float2 _UVMin;
float2 _UVMax;
float2 vertexToUV(float4 vertex)
{
return
(vertex.xz - _VertexMin) / (_VertexMax - _VertexMin)
* (_UVMax - _UVMin) + _UVMin;
}Теперь мы можем вызывать функцию
getVertex без необходимости передачи ей v.texcoord:float4 getVertex(float4 vertex)
{
float3 normal = float3(0, 1, 0);
float2 texcoord = vertexToUV(vertex);
fixed height = tex2Dlod(_HeightMap, float4(texcoord, 0, 0)).r;
vertex.xyz += normal * height * _Amount;
return vertex;
}Тогда вся функция
vert принимает вид:void vert(inout appdata_base v)
{
v.vertex = getVertex(v.vertex);
}Эффект прокрутки
Благодаря написанному нами коду на меше отображается вся карта. Если мы хотим усовершенствовать отображение, то нужно внести изменения.
Давайте ещё немного формализуем код. Во-первых, нам может понадобиться приблизить отдельную часть карты, а не смотреть на неё целиком.
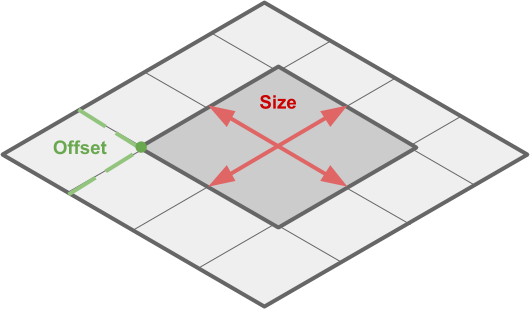
Эту область можно определить двумя значениями: её размерами (
_CropSize) и расположением на карте (_CropOffset), измеряемыми в пространстве вершин (от _VertexMin до _VertexMax).// Cropping
float2 _CropSize;
float2 _CropOffset;Получив эти два значения, мы можем ещё раз использовать линейную интерполяцию, чтобы
getVertex вызывалась не для настоящей позиции вершины 3D-модели, а для отмасштабированной и перенесённой точки.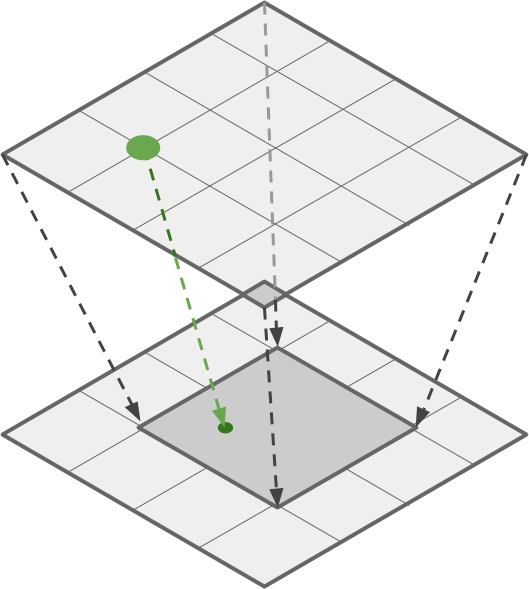
Соответствующий код:
void vert(inout appdata_base v)
{
float2 croppedMin = _CropOffset;
float2 croppedMax = croppedMin + _CropSize;
// v.vertex.xz: [_VertexMin, _VertexMax]
// cropped.xz : [croppedMin, croppedMax]
float4 cropped = v.vertex;
cropped.xz = (v.vertex.xz - _VertexMin) / (_VertexMax - _VertexMin)
* (croppedMax - croppedMin) + croppedMin;
v.vertex.y = getVertex(cropped);
}Если мы хотим, чтобы выполнялась прокрутка, то достаточно будет обновлять
_CropOffset через скрипт. Благодаря этому область усечения будет двигаться, фактически выполняя прокрутку по ландшафту.public class MoveMap : MonoBehaviour
{
public Material Material;
public Vector2 Speed;
public Vector2 Offset;
private int CropOffsetID;
void Start ()
{
CropOffsetID = Shader.PropertyToID("_CropOffset");
}
void Update ()
{
Material.SetVector(CropOffsetID, Speed * Time.time + Offset);
}
}Чтобы это сработало, очень важно указать для режима Wrap Mode всех текстур значение Repeat. Если этого не сделать, то мы не сможем зацикливать текстуру.
Для эффекта отдаления/приближения достаточно будет просто изменять
_CropSize.Часть 3. Затенение рельефа
Плоское затенение
Весь написанный нами код работает, но имеет серьёзную проблему. Затенение модели выполняется как-то странно. Поверхность правильно искривляется, но реагирует на свет так, как будто является плоской.
Это очень чётко видно на показанных ниже изображениях. На верхнем изображении показан имеющийся шейдер; на нижнем показано, как он работает на самом деле.


Устранение этой проблемы может быть большой сложностью. Но сначала нам нужно разобраться, в чём же ошибка.
Операция экструдирования нормалей изменила общую геометрию плоскости, которую мы использовали изначально. Однако Unity изменила только позицию вершин, но не их направления нормалей. Направление нормали вершины, как понятно из названия, — это вектор единичной длины (направление), указывающий перпендикулярно поверхности. Нормали необходимы, потому что они играют важную роль в затенении 3D-модели. Они используются всеми поверхностными шейдерами для вычисления того, как свет должен отражаться от каждого треугольника 3D-модели. Обычно это нужно для улучшения трёхмерности модели, например, это заставляет свет отражаться от плоской поверхности так же, как он отражался бы от изогнутой. Этот трюк часто используется, чтобы низкополигональные поверхности выглядели более плавными, чем есть на самом деле (см. ниже).

Однако в нашем случае происходит обратное. Геометрия искривлённая и плавная, но так как все нормали направлены вверх, свет отражается от модели так, как будто она плоская (см. ниже):

Подробнее о роли нормалей в затенении объекта можно прочитать в статье о Normal Mapping (Bump Mapping), где одинаковые цилиндры выглядят очень разными, несмотря на одну 3D-модель, из-за разных способов вычислений нормалей вершин (см. ниже).


К сожалению, ни в Unity, ни в языке создания шейдеров нет встроенного решения для автоматического пересчёта нормалей. Это значит, что придётся изменять их вручную в зависимости от локальной геометрии 3D модели.
Вычисление нормалей
Единственный способ устранения проблемы с затенением — это вычисление нормалей вручную на основании геометрии поверхности. Подобная задача рассматривалась в посте Vertex Displacement – Melting Shader Part 1, где она использовалась для симуляции таяния 3D-моделей в игре Cone Wars.
Хотя готовый код должен будет работать в 3D-координатах, давайте пока ограничим задачу только двумя измерениями. Представим, что на нужно вычислить направление нормали, соответствующей точке на 2D-кривой (большая синяя стрелка на схеме ниже).
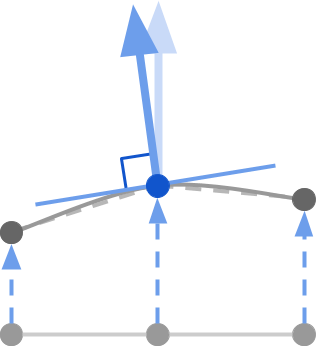
С геометрической точки зрения, направление нормали (большая синяя стрелка) — это вектор, перпендикулярный касательной, проходящей через интересующую нас точку (тонкую синюю линию). Касательную можно представить как линию, расположенную на кривизне модели. Касательный вектор — это единичный вектор, который лежит на касательной.
Это значит, что для вычисления нормали нужно сделать два шага: сначала найти прямую, касательную к нужной точке; затем вычислить вектор, перпендикулярный ей (который и будет необходимым направлением нормали).
Вычисление касательных
Для получения нормали нам сначала нужно вычислить касательную. Её можно аппроксимировать, сэмплировав точку поблизости и использовав его для построения отрезка рядом с вершиной. Чем меньше отрезок, тем точнее будет значение.
Необходимы три этапа:
- Этап 1. Сдвинуться на небольшую величину по плоской поверхности
- Этап 2. Вычислить высоту новой точки
- Этап 3. Использовать высоту текущей точки для вычисления касательной
Всё это можно увидеть на изображении ниже:
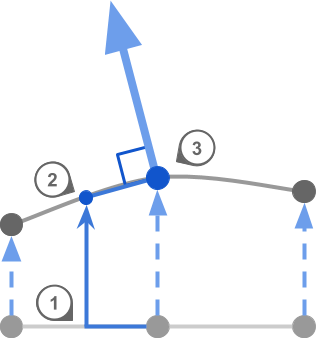
Чтобы это сработало, нам нужно вычислить высоты двух точек, а не одной. К счастью, мы уже знаем, как это сделать. В предыдущей части туториала мы создали функцию, сэмплирующую высоту ландшафта на основании точки меша. Мы назвали её
getVertex.Мы можем взять новое значение вершины в текущей точке, а затем ещё в двух других. Одна будет для касательной, другая — для касательной в двух точках. С их помощью мы получим нормаль. Если исходный меш, который использовался для создания эффекта, является плоским, (а в нашем случае так и есть), то нам не нужен доступ к
v.normal и мы можем просто использовать для касательной и касательной к двум точкам соответственно float3(0, 0, 1) и float3(1, 0, 0). Если бы мы хотели сделать то же самое, но, например, для сферы, то найти две подходящие точки для вычисления касательной и касательной к двум точкам было бы намного сложнее.Векторное произведение
Получив подходящие векторы касательной и касательной к двум точкам, мы можем вычислить нормаль при помощи операции под названием векторное произведение. Существует множество определений и объяснений векторного произведения и того, что оно делает.
Векторное произведение получает два вектора и возвращает один новый. Если два исходных вектора были единичными (их длина равна единице), и они расположены под углом 90, то получившийся вектор будет расположен под 90 градусов относительно обоих.
Поначалу это может сбивать с толку, но графически это можно представить так: векторное произведение двух осей создаёт третью. То есть , но ещё и , и так далее.
Если мы сделаем достаточно малый шаг (в коде это
offset), то векторы касательной и касательной к двум точкам будут находиться под углом 90 градусов. Вместе с вектором нормали они образуют три перпендикулярные оси, ориентированные вдоль поверхности модели.Зная это, мы можем написать весь необходимый код для вычисления и обновления вектора нормали.
void vert(inout appdata_base v)
{
float3 bitangent = float3(1, 0, 0);
float3 tangent = float3(0, 0, 1);
float offset = 0.01;
float4 vertexBitangent = getVertex(v.vertex + float4(bitangent * offset, 0) );
float4 vertex = getVertex(v.vertex);
float4 vertexTangent = getVertex(v.vertex + float4(tangent * offset, 0) );
float3 newBitangent = (vertexBitangent - vertex).xyz;
float3 newTangent = (vertexTangent - vertex).xyz;
v.normal = cross(newTangent, newBitangent);
v.vertex.y = vertex.y;
}Соединяем всё вместе
Теперь, когда всё работает, мы можем вернуть и эффект прокрутки.
void vert(inout appdata_base v)
{
// v.vertex.xz: [_VertexMin, _VertexMax]
// cropped.xz : [croppedMin, croppedMax]
float2 croppedMin = _CropOffset;
float2 croppedMax = croppedMin + _CropSize;
float4 cropped = v.vertex;
cropped.xz = (v.vertex.xz - _VertexMin) / (_VertexMax - _VertexMin)
* (croppedMax - croppedMin) + croppedMin;
float3 bitangent = float3(1, 0, 0);
float3 normal = float3(0, 1, 0);
float3 tangent = float3(0, 0, 1);
float offset = 0.01;
float4 vertexBitangent = getVertex(cropped + float4(bitangent * offset, 0) );
float4 vertex = getVertex(cropped);
float4 vertexTangent = getVertex(cropped + float4(tangent * offset, 0) );
float3 newBitangent = (vertexBitangent - vertex).xyz;
float3 newTangent = (vertexTangent - vertex).xyz;
v.normal = cross(newTangent, newBitangent);
v.vertex.y = vertex.y;
v.texcoord = float4(vertexToUV(cropped), 0,0);
}И на этом наш эффект наконец-то завершён.

Куда двигаться дальше
Этот туториал может стать основой более сложных эффектов, например, голографических проекций или даже копии песочного стола из фильма «Чёрная пантера».
Пакет Unity
Полный пакет для этого туториала можно скачать на Patreon, он содержит все ассеты, необходимы для воспроизведения описанного эффекта.


Normal_Mur
Mesh.RecalculateNormals — пересчитывает нормали.
Для создания эффекта острых углов достаточно разделить меш на треугольники так, чтобы для каждого angle был свой vertice.