Хорошая гипотеза притягивает ум математика. Она говорит о чем-то сложном и глубоком точно и лаконично, требуя доказательства или опровержения. Перед хорошей формулой тяжело устоять.
Но выдвинуть красивую гипотезу сложно. Все самые элегантные и естественные, вроде гипотезы Эйлера, теоремы Ферма, формулы Римана — были предложены ещё сотни лет назад. Для развития математики ей нужны новые проблемы. И новые формулы, доказательства к которым можно было бы находить.
Для этого группа исследователей из института Технион в Израиле вместе с Google создала автоматизированную систему генерации математических гипотез. Её назвали «Машиной Рамануджана» — в честь знаменитого математика начала XX века, разработавшего тысячи новаторских формул почти без формального обучения. Программа уже выдвинула несколько оригинальных и важных уравнений для некоторых математических констант, а вокруг машины уже развивается активное математическое сообщество. Научный труд ученых был опубликован на прошлой неделе в журнале Nature.

Сриниваса Рамануджан — в центре
Машина Рамануджана не берет на себя доказательство гипотез. Она предназначена быть своего рода «кормушкой» для существующих математиков. Как объясняют исследователи в своей статье, всю отрасль математики можно, грубо говоря, разбить на два процесса: предположения и доказательства. Чем больше гипотез — тем больше материи для развития математического ума, поводов для проведения дальнейших математических исследований. Но находить их сейчас человеку почти невозможно, нужна огромная удача. Без помощи алгоритмов на составление одной красивой, полезной и правдоподобной формулы может уйти несколько десятков лет.
Ученые в своей статье говорят, что особенно полезными при поиске гипотез оказались два алгоритма: метод встречи посередине и алгоритм оптимизации градиентного спуска. Они оба работают путем сопоставления ожидаемых и полученных числовых значений. Машина строит гипотезы о формулах, не зная, есть ли у них решения, и не опираясь ни на какие предыдущие знания. Она просто «чувствует», что формула подходящая, и видит, что она хорошо предсказывает требуемый результат.
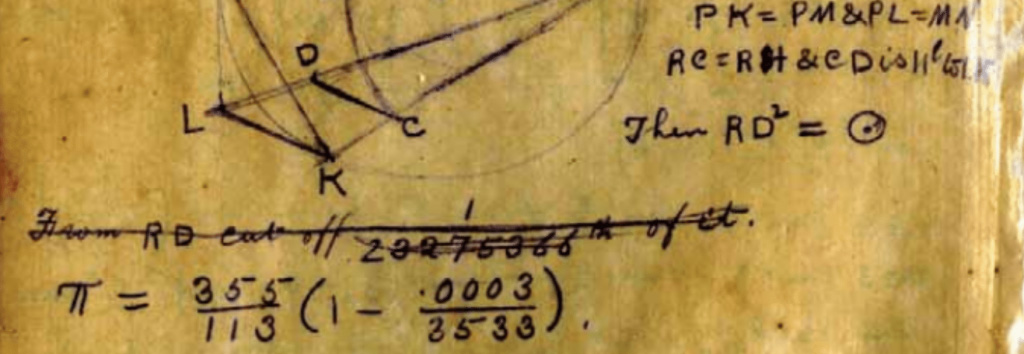
Записки Рамануджана, начало XX века
Исследователи из Техниона говорят, что их алгоритмы «могут заменить интуицию великих математиков, и открыть новые проблемы для будущих поколений». Сейчас машина выдвигает предположения о формулах, идеально описывающих значения универсальных иррациональных математических констант (например, Пи, e, ?, постоянной Апери, G, ?, log(2) и так далее). Такие константы у неё записываются в виде непрерывных дробей — то есть, дробей, знаменатель которых состоит из суммы двух членов, второй из которых сам является дробью, знаменатель которой тоже содержит два члена (один из которых является дробью, которая… и так до бесконечности).
Как это работает
Непрерывные дроби давно привлекают математиков сочетанием внешней простоты и внутренней глубины. Помимо того, что они «по своей природе очаровательны» эстетикой, они также полезны для определения фундаментальных свойств констант, как выяснили в марте 2020 года Роберт Доуттери-Блисс и Дорон Зейлбергер из Ратгерского университета в США.
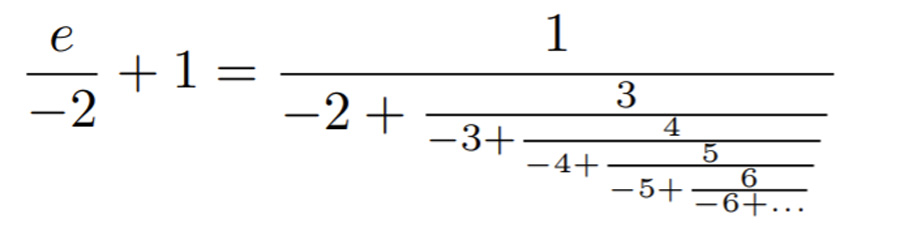
Одна из найденных формул
Машина Рамануджана находит формулы непрерывных дробей, которые с очень большой точностью кажутся равными универсальным константам. Эта высокая достоверность (вплоть до триллионных значений) — крайне важна, иначе предположения были бы легко отброшены и не имели бы большой ценности.
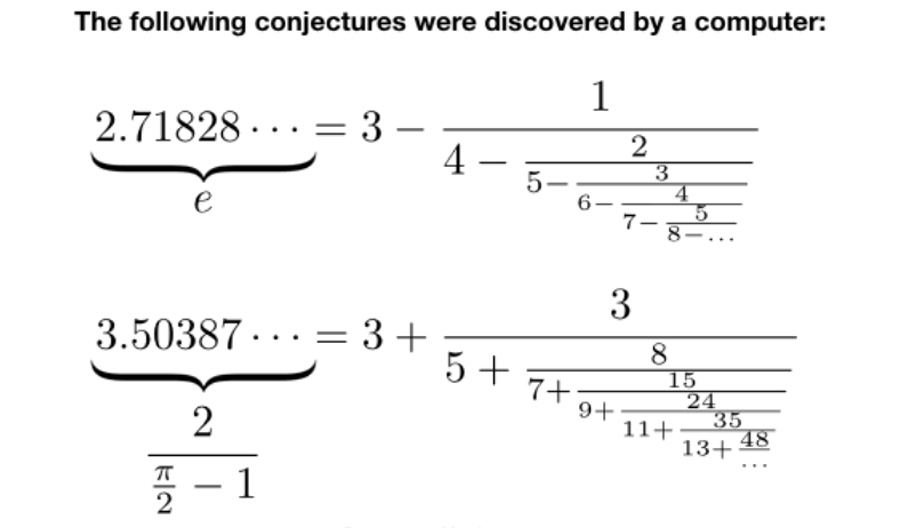
Каждая гипотеза принимает форму уравнения. Слева — формула, включающая универсальную константу. Справа — непрерывная дробь. Один из алгоритмов в машине проверяет их совпадение, и если чувствует, что за что-то зацепился, пытается найти более точную формулу. Второй — как обычно, пытается его опровергнуть, найдя несоответствие. Если кажется, что значения с двух сторон от знака равенства всегда совпадают, формула рассчитывается с более высокой точностью. Если ошибки не найдено, итоговая гипотеза выдается на обсуждение и решение людям.
Потом математики могут использовать эти предположения для реинжиниринга скрытых теорем или поиска более элегантных результатов, как уже показали исследования из Ратгерского университета.
Результаты
Самое заметное открытие исследователей — новая гипотеза удивительной важности. Несколько выражений (pdf), созданных Машиной, способны вычислять значение числа Каталана более эффективно, чем все предыдущие формулы, открытые человеком. Точное значение этой постоянной необходимо для решения многих математических задач.
Новые выражения в виде непрерывной дроби позволяют максимально быстро вычислить число Каталана (G). Для проверки предыдущих формул на компьютере требовалось в разы больше времени.
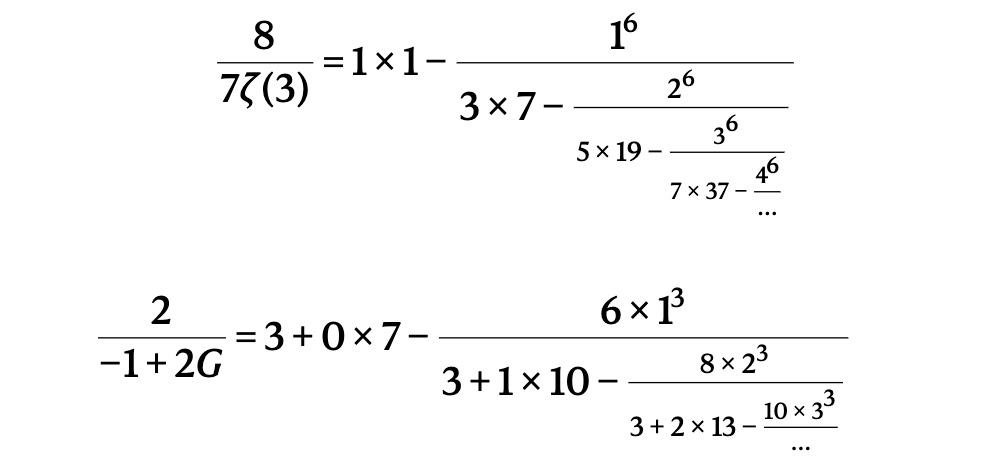
Основная работа ведется на сайте http://www.ramanujanmachine.com/. Новые найденные гипотезы добавляются в специальный раздел. На данный момент машина нашла около сорока правдоподобных гипотез для вычисления числа Пи и 25 новых формул, описывающих e, число Эйлера. А также под сотню других формул для быстрого вычисления различных иррациональных математических констант.
Как можно помочь
Исследователи пригласили математическое сообщество помочь развитию Машины Рамануджана. Сделать это можно одним из трех способов:
- Запустить машину Рамануджана у себя на компьютере. Для этого у них есть GitHub с кодом Python. Формула, найденная вашей машиной, будет названа вашим именем. Например, Пол Михальски нашел новую, ранее неизвестную формулу вычисления Пи, а Чжу Хэ — уравнение, включающее log(2). Ученые также работают над распределенным приложением на основе BOINC, которое позволит автоматически запускать машину каждый раз, когда компьютер простаивает.
- Попытаться доказать предположения машины. Алгоритмы обнаруживают математические формулы, но не доказывают их. Можно попытаться доказать их предположения и внести свой вклад в математику, отправив ссылку с PDF/DOC/TXT-файл с доказательством к ним на сайт.
- Предложить или разработать свои алгоритмы. Если у вас есть идеи по улучшению алгоритмов для поиска математических формул, можно предложить их на GitHub проекта. Разработка длится уже несколько лет, она началась задолго до официальной публикации в Nature, и команда считает, что машине ещё есть, куда расти.
Раньше компьютеры эффективнее нас решали готовые задачи. Теперь они оказались лучше людей и в составлении гипотез.



Sdima1357
Ученики занимались этими упражнениями по шесть часов в день, и профессор показал мне множество фолиантов, составленных из подобных отрывочных фраз; он намеревался связать их вместе и от этого богатого материала дать миру полный компендий всех искусств и наук; его работа могла бы быть, однако, облегчена и значительно ускорена, если бы удалось собрать фонд для сооружения пятисот таких станков в Лагадо и обязать руководителей объединить полученные ими коллекции.
Он сообщил мне, что это изобретение с юных лет поглощало все его мысли, что теперь в его станок входит целый словарь и что им точнейшим образом высчитано соотношение числа частиц, имен, глаголов и других частей речи, употребляемых в наших книгах.
Я принес глубочайшую благодарность этому почтенному мужу за его любезное посвящение меня в тайны своего великого изобретения и дал обещание, если мне удастся когда-нибудь вернуться на родину, воздать ему должное как единственному изобретателю этой изумительной машины, форму и устройство которой я попросил у него позволения срисовать на бумаге и прилагаю свой рисунок к настоящему изданию. Я сказал ему, что в Европе хотя и существует между учеными обычай похищать друг у друга изобретения, имеющий, впрочем, ту положительную сторону, что возбуждает полемику для разрешения вопроса, кому принадлежит подлинное первенство, тем не менее я обещаю принять все меры, чтобы честь этого изобретения всецело осталась за ним и никем не оспаривалась.
:: Джонатан Свифт. Путешествия Лемюэля Гулливера
alexxz
"В сущности, это очень просто. Мы составляем список, который включит в себя все возможные имена бога." 9 миллиардов имён бога. Артур Кларк.
"Высоко над ними, тихо, без шума, одна за другой гасли звезды."
Sdima1357
Очень красивый рассказ, мне он тоже очень нравится, но он навеян легендой о ханойской башне.
en.m.wikipedia.org/wiki/Tower_of_Hanoi
amarao
Чувство прекрасного у этой машины так себе. Я знаю, что цепные дроби вызывают у некоторых людей очарование, но я обычно содрогаюсь от мысли о размере формул, связанных с "суммированием в знаменателе".
А вот пример красоты (робот, где такое же?):
F + V = E + 2
Или вот:
e^ix = cos x + i sin x
alexxz
Я раньше тоже содрогался от этих дробей и не понимал какое такое больное сознание их придумало. А вот недавно посмотрел видео от Mathologer и все стало на свои места и обрело смысл. https://youtu.be/WL_Yzbo1ha4
lpssp
Что-то кажется они создали машину, которая может подбирать цепные дроби для констант.
То-есть решает одну конкретную задачу, а не делает какие-то новые предположения, как это делали великие математики.
Тоесть вот это утверждение:
выглядит как просто PR чистейшей воды и никаких великих математиков она конечно не заменит. Да и новые проблемы врядли откроет.
Ну, если под составлением гипотез автор понимает составление цепных дробей для констант, то возможно.
А так хотелось бы конечно убавить оттенки желтого в статье :).
speakingfish
Какие-то частности.
Как будто и не было Дугласа Лената с его AM 1977 года, или более позднего Eurisko 1980 года.
Flux
Лютый кликбейт, вся "статья" ради баннера в футере (впрочем, как и всегда в корпоративных блогах).
Вы бы хоть имели совесть не употреблять фразу "изобретение математики" для скрипта поиска цепных дробей. Но какая там совесть и уважение к математикам если на кону стоят просмотры, правда?
Dr_Faksov
А доказательства опять будут вида — " Я всё проверил, ошибок нет, мамой клянусь!"
GeMir
vics001
Да, какое-то внутреннее чувство, формула простая, поэтому проверять нужно до 50 знака. И ведь никак не опровергнешь.
Только если чисто с теории вероятности, что простая формула будет ошибаться в 50 знаке, вероятность встретить ее в жизни равно 0 :-)
Dr_Faksov
Что такое 50-й знак? Ни-че-го!
Уж не помню кто из знаменитых рассказывал, что считали они сходимость вроде. Дошли до предела разрядности машины, а ряд не сходится, хотя в теории должен. И спасла их аналоговая машина. Оказалось что ряд начинает сходится где-то после 1800-го знака.
А вы говорите — 50-й…
technic93
Я понимаю что математикам надо рекламировать свою программу чтобы люди запускали ее у себя на компьютере. Но с каждой итерацией репостов заголовок всё желтее и желтее. Узко специализированная задача преподносится как ответ 42.