Введение: зачем нужна линейная алгебра в 3D и операции над векторами.

Это первый, вводный урок по линейной алгебре для разработки 3D-приложений от Александра Паничева — ведущего разработчика логики в UNIGINE. В этом уроке разберемся зачем 3D-разработчикам вообще нужна линейная алгебра, а также рассмотрим основные операции над векторами.

Во втором уроке будут разобраны более сложные темы: углы Эйлера, кватернионы и матрицы.

Почему именно линейная алгебра?

Во-первых, в любом 3D-приложении мы так или иначе сталкиваемся с векторами и вращениями. Vector, Matrix — об этих терминах слышали все. Мы двигаем объекты, поворачиваем их на определенные градусы, вытаскиваем в процессе всякую полезную информацию для дальнейших вычислений… Поэтому умение оперировать с ними быстро и эффективно, минуя лишнюю тригонометрию там, где она не нужна, крайне важно!

Во-вторых, даже после работы в геодезических координатах все сводится к обычному трехмерному евклидову пространству. Таков уж рендер: простой, не кривой. Поэтому знать линал — основа жизни 3D-шника!

А кроме того, у многих знания по математике обрывочные. Надо заполнить пробелы!

Из чего состоит математическая библиотека 3D-движка?

В игровых движках обычно есть 3 группы:

1. Вектора. Может быть точкой, радиус-вектором, направлением (нормаль), линейной скоростью, угловой скоростью, углами в градусах или радианах (углах Эйлера).

Вектор-точка — просто позиция в пространстве. Радиус-вектор означает, что его начало находится в 0 относительно начала координат. Направление — это нормализованный вектор, который можно назвать радиус-вектором фиксированной (единичной) длины. Линейная скорость и угловая скорость отвечают за динамику. А углы Эйлера подробно разберем во втором уроке.

2. Матрицы. Матрица смещения, матрица вращения, матрица масштабирования, матрица трансформации (TRS), проекции (перспективная, ортографическая), система линейных алгебраических уравнений, матрица Якоби и Тензор инерции, матрица гомографии.

Матрица гомографии используется в камерах для правильной проекции с разных углов обзора.

3. Кватернионы. Вращение, выраженное в кватернионах.

Через что можно представить ориентацию объекта?

1. Матрица вращения 3х3 (Matrix 3x3). Чтобы получить поворот, достаточно перемножить матрицу вращения на вектор или на матрицу трансформации. Но возникают проблемы, когда нужно плавно вращать объект из одних углов в другие — простыми способами это не сделать. Кроме того, легко накапливаются ошибки округлений, если много раз перемножать матрицу. В результате объект становится скошенным (ромбообразным).

2. Углы Эйлера (Euler Angles). Состоят из крена (Roll), тангажа (Pitch) и рысканья (Yaw). С этим легко разобраться и легко представить. Интерполяция вокруг одной оси тоже делается легко, но интерполяция по двум осям будет происходить не по кратчайшему пути, а по S-образной кривой. Кроме того, удобно ограничивать вращение сочленений в градусах. Главный недостаток — шарнирный замок (о нем позже).

3. Ось-Вращение (Axis – Angle). Простой метод с простой интерполяцией и удобным ограничением вращения. Однако с помощью него неудобно складывать несколько вращений вместе, чтобы получить единый объект вращения.

4. Кватернионы (Quaternion). Можно представить, как точку на поверхности трисферы единичного радиуса в четырехмерном пространстве. Легко складываются вращения, интерполяция идет по кратчайшему пути. Нет такого недостатка, как шарнирный замок. Просто ограничивать вращение. Однако сложны для прочтения. Кроме того, накапливают ошибку при многоразовом перемножении — нужно периодически нормализовать.

5. Экспоненциальное отображение (Exponential Map). Напоминает Ось-Вращение. Легко складывать вращения. Меньше степеней свободы, поэтому годится только как динамика вращения.

6. 6-мерное представление (6D Representation). Зачастую случайно получается в конце вычислений. Часто используется в нейросетях. По сути — две оси: Forward и Up. Используется как основа для создания матрицы 3x3.

Кстати…

Для x нужно взять cos от угла, а для y — sin от угла. Также можно использовать функцию atan2, которая работает в диапазоне от -π до π.

Пару слов про производительность мат. функций

Сложение (plus), вычитание (minus), умножение (mult) и деление (div) занимает примерно одно время. А, например, вычисление квадратного корня (sqrt) в 3,6 медленнее. Самое медленное: аркосинусы (acos), арксинусы (asin), арктангенсы (atan) и округление (round).

Выводы:

1. Тригонометрия очень медленная. Особенно та, что возвращает углы.

2. Взятие квадратного корня (sqrt) по скорости примерно как 6 умножений (6_mult).

3. Вычисление наибольшего элемента (max) и округление (round), внезапно, сильно медленные.

Операции над векторами в 2D

Основные: сложение векторов, вычитание векторов, умножение вектора на скаляр и нормализация вектора. У них внутри простой код с простой нормализацией и взятием длины.

Пример. Есть персонаж, он стоит в начале координат и хочет добежать до дерева. В этом примере можно использовать все 4 базовые операции:

vec2 pos = vec2(2,2); // позиция персонажа
vec2 tree = vec2(6,4); // позиция дерева
vec2 distance = tree - pos // radius vector
vec2 direction = distance.normalize(); // нормализованный unit vector

vec2 new_pos = pos + direction * IFps // берем старую позицию и умножаем вектор на скаляр

dot product — скалярное произведение векторов

Это операция над двумя векторами, результатом которой является скаляр:

float dot(vec2 v0, vec2 v1) { v0.x * v1.x + v0.y * v1.y; // 2 умножения, 1 сложение }

1. Равен произведению длин векторов на косинус угла между ними:

dot(a,b) = |a||b|cos(angle_rad)

2. Скалярное произведение > 0, если вектора направлены в одну сторону, 0 — если вектора перпендикулярны и < 0, если направлены противоположно.

3. Является длиной проекции произвольного вектора на нормализованный вектор:

proj_length = dot(a, normal)

4. Скалярное произведение самого на себя является квадратом длины вектора:

dot(a,a) == length2(a)

5. Получить вектор-проекцию можно так:

proj_point = b*dot(a,b)/dot(b,b)

6. dot(a,b) == dot(b,a)

Где еще используется dot?

А как найти перпендикуляр?

В 2D все просто: переставляем (x,y) местами и у какого-нибудь компонента меняем знак. Например, для поворота по часовой стрелке нужно поставить минус у второго компонента, а против часовой — у первого.

А если совместить dot и нахождение перпендикуляра?

Для этого есть операция skew product — косое произведение векторов. Это операция над двумя векторами, результатом которой является псевдоскаляр:

float skew(vec2 v0, vec2 v1) { v0.x * v1.y - v0.y * v1.x; // 2 умножения, 1 вычитание }

В UNIGINE такая операция называется cross.

Где еще используется skew?

Операции над векторами в 3D

Работа с векторами в 3D мало чем отличается от 2D. Можно сказать, что решив задачу в 2D, вы решите ее и в 3D. Так, например, скалярное произведение векторов dot product, о котором речь ниже, одинаково работает в 2D и 3D.

Но в 3D появляется операция cross product — векторное произведение векторов. О нем поговорим в конце главы.

Где еще используется dot в 3D?

В шейдерах. Повсеместно. Например, рассмотрим простейшую модель освещения Ламберта (Lambert, Lambertian Reflectance, или Diffuse Light):

У нас есть модель с набором нормалей и где-то источник света.

Просто вычисляем угол между источником света и нормалью поверхности. Чем меньше угол, тем ярче пиксель.

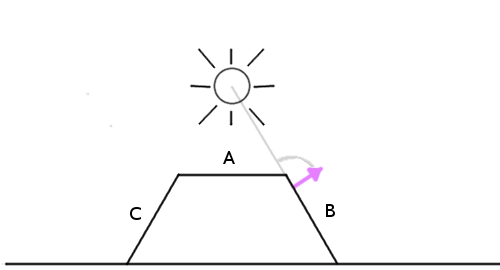
Вот как выглядит алгоритм:

1. Получаем вектор нормали текущего пикселя — NormalVector.

2. Получаем вектор направления света относительно текущего пикселя — LightVector.

3. Нормализуем векторы.

4. Вычисляем угол между ними — dot.

5. Умножаем конечный цвет на этот коэффициент и коэффициент затухания.

float diffuse = max(dot( LightVector, NormalVector ), 0.0);
float attenuation = saturate(1.0 - DistanceToLight / LightRadius);

FragColor = color * diffuse * attenuation;

cross product — векторное произведение векторов

cross product появляется в 3D-пространстве. Это операция над двумя векторами, результатом которой является вектор, перпендикулярный исходным двум:

vec3 cross(const vec3 &v0, const vec3 &v1)
{
    vec3 ret;
    ret.x = v0.y * v1.z - v0.z * v1.y;
    ret.y = v0.z * v1.x - v0.x * v1.z;
    ret.z = v0.x * v1.y - v0.y * v1.x;
    return ret; // 6 умножений, 3 вычитания
}

1. Длина результирующего вектора равна площади параллелограмма, образованного исходными векторами.

2. Длина результата — это еще и |a||b|sin(angle_rad)

3. Перпендикуляр строится по правилу «правой руки».

4. Не коммутативен. То есть: cross(a,b) != cross(b,a)

Если вам вдруг интересно как потом этот результат можно использовать для вращения тела:

vec3 torque; // крутящий момент
quat rotation; // текущее вращение тела

// qnew = q0 + 0.5 * w * q0
quat q = (rotation + quat(torque * ifps) * rotation * 0.5f).normalize();

Конечно, задачу с танком можно решить и через:

vec3 rel_pos =
    inverse(tank_transform_mat4) * vec3_target_position;

Если известна обратная матрица, то такой способ будет примерно равен по скорости комбинации dot(cross).

Но… Не всегда у нас есть обратная матрица на руках. Мы можем быть в процессе изменения направления. Да и не всегда есть матрица как таковая.

Fun fact: Помните задачу нахождения отраженного вектора? Зная ее, можно легко то же самое сделать через dot (еще и быстрее будет работать!):

vec3 new_dir = dir - normal * dir(dir, normal);

dot(cross()) — scalar triple product, смешанное произведение

Скалярное произведение вектора a на векторное произведение векторов b и c

float scalar_triple(const vec3 &a, const vec3 &b, const vec3 &c)
{
    // 9 умножений, 5 сложений
    return dot(a, cross(b, c));
}

1. Модуль смешанного произведения численно равен объему параллелепипеда, образованного векторами a,b,c.

2. dot(a,cross(b,c)) == dot(cross(a,b),c)

3. Равен детерминанту (определителю) матрицы, составленной из векторов a,b,c. В том числе и по перфу.

4. Аналог skew в мире 3D.

* * *

На этом пока все. Во втором уроке разберем сложные темы: углы Эйлера, кватернионы и матрицы.