04.05.2023 08:36
alexlyk314 10 1800 Источник

Как найти площадь произвольного многоугольника с вершинами в узлах клетчатой бумаги?

В простых ситуациях его можно разбить на треугольники (рис. 1а) или, наоборот, достроить до прямоугольника (рис. 1б). Но как быть в общем случае? Посмотрите, скажем, на рисунок 1в.

Оказывается, достаточно подсчитать числоIвершин внутри многоугольника и число Bна его границе — тогда его площадьSбудет равна

S = I + \frac B 2 − 1.

Это формула называется формулой Пика в честь австрийского математика Георга Пика (1859–1942), открывшего её в 1899 году. Так, для многоугольника на рисунке 1в имеем

I = 13, B = 20, поэтому S = 13 + \frac {20} {2} − 1 = 22.

Формула выглядит удивительно просто. Интересно, столь же просто её доказать?

Этап 1: ШАГ ИНДУКЦИИ. Предположим, что многоугольник разбит диагональю на два, для которых формула доказана. Тогда несложно показать, что она верна и дляM.

Этап 2: ТРИАНГУЛЯЦИЯ. Многократно проводя внутренние диагонали, разобьём наш многоугольник на элементарные треугольники (не содержащие узлов ни на границе, ни внутри, кроме вершин). Для такого треугольника I = 0 иB = 3,поэтому площадь должна быть равнаS = 1/2.

Этап 3: БАЗА ИНДУКЦИИ. Остаётся доказать, что площадь элементарного треугольника равна1/2.Мы приведём важное и красивое рассуждение.

Пусть треугольник имеет вершины (0, 0), (a, b)и(c, d).Достроим его до параллелограмма, добавив вершину (a + c, b + d),и замостим его копиями всю плоскость (рис. 2).

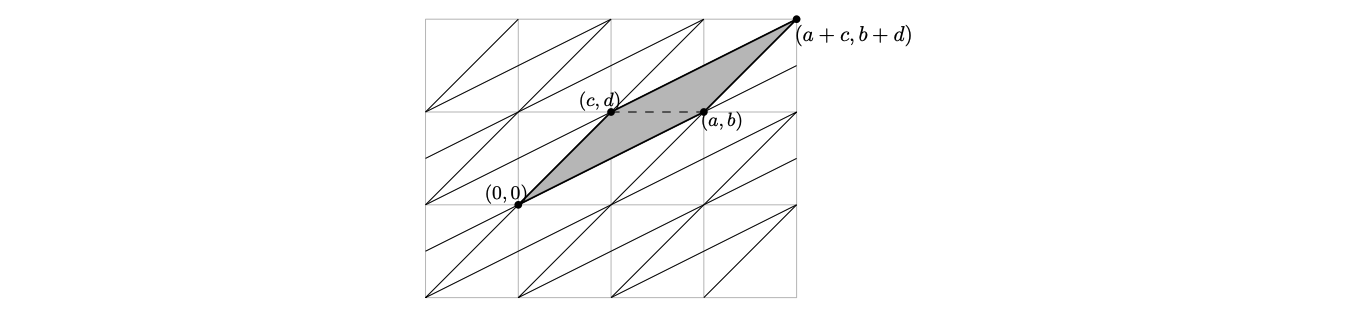
Элементарность нашего треугольника равносильна тому, что любой узел(e, f)можно получить из узла(0, 0)целочисленными сдвигами сторон(a, b)и(c, d).Иными словами, для любых целыхeиfнайдутся целыеxиyтакие, что

x(a, b) + y(c, d) = (e, f) \Longleftrightarrow \begin{cases} ax + cy = e \\ bx + dy = f. \end{cases}

Неожиданно, геометрическая задача свелась к чисто алгебраической — системе линейных уравнений. Её решение даётся формулами Крамера

x = \frac {de − cf} ∆ , \;\; y = \frac {af − be} ∆ , \;\;где \;\; ∆ = ad − bc \;\; — \;\; \textit {определитель} \;\;системы .

Хорошо известно, что определитель∆по модулю равен площади параллелограмма, построенного на векторах(a, b)и(c, d),поэтому нам надо доказать, что∆ = ±1.
При(e, f) = (1, 0)имеем(x, y) = (d/∆, −b/∆),а при
(e, f) = (0, 1) - (x, y) = (−c/∆, a/∆).Так какx, yвсегда должны быть целыми, то a, b, c, dкратны∆откуда∆ = ad − bcкратно ∆^2, что возможно, лишь при ∆ = ±1.Формула Пика доказана.

В заключение сделаем несколько замечаний.

  • Приведённое рассуждение с замещением плоскости на школьном языке иллюстрирует важные идеи высшей алгебры — описание базисов свободной абелевой группы\mathbb Z^2и группы её автоморфизмов:

    Aut(\mathbb Z^2) \; \cong \; GL_2 (\mathbb Z)=\left\{\begin{pmatrix} a & b \\ c & d \end{pmatrix} \middle| ad-bc=\pm 1 \right\}.

  • Последний факт можно обобщить на высшие размерности: Aut(\mathbb Z^n) \; \cong \; \{ {A| det \;A = ±1} \}.

  • А вот формула Пика неверна уже в трёхмерном пространстве: объём многогранника с целыми вершинами не выражается через количества вершин внутри, на гранях и рёбрах.

  • Вместе с тем существуют варианты обобщения формулы Пика для некоторых классов целочисленных многомерных многогранников (например, с центрально-симметричными гранями).

Автор: Андрей Канунников, к. ф.-м. н., мехмат МГУ, преподаватель ШАД Хелпер

Комментарии (10)