15.08.2023 11:31
anikengur 0 300 Источник

Данная статья является продолжением "Рекомендательная система SVD". Если вам не знакома терминология (user-item matrix, SVD-разложение, PCA, метод главных компонент и пр.), то рекомендую прежде прочитать первую часть.

Netflix Prize - одно из самых известных соревнований в области машинного обучения. Целью было создание алгоритма, который улучшал бы рекомендации фильмов и телешоу на 10%.

Один из наиболее успешных алгоритмов был алгоритм Саймона Фанка, основной идеей которого является матричная факторизация.

Матричная факторизация - разложение матрицы на произведение двух или более матриц. Например, SVD-разложение.

Пусть у нас имеется матрица рейтингов пользователей R (разряженная user-item matrix). r_{ui}- элементы R. Обозначим через \hat R- прогнозируемые рейтинги и \hat r_{ui}- элементы \hat R. Представим R как произведение матриц Pна Q. Подразумевается, что P- скрытые факторы пользователя (user), p_u- u-ая строка. Q- скрытые факторы элемента (item), q_i- i-ый столбец (такие методы называют Latent Models for Collaborative Filtering). Тогда прогнозируемый рейтинг для u-го пользователя и i-го товара вычисляется как скалярное произведение: \hat r_{ui} = q^T_i p_u.

Обучение состоит в минимизации квадратичной ошибки:

\sum_{r_{ui} \in R_{train}} \left(r_{ui} - \hat{r}_{ui} \right)^2 +\lambda \left(||q_i||^2 + ||p_u||^2\right)

где \lambda - некоторый коэффициент (гиперпараметр).

Однако, при прогнозировании оценок необходимо учитывать предубеждения пользователей.

Например, пользователь, вероятно, поставит более завышенную оценку фильму, который признан каким-то сообществом. В то время как менее популярный фильм получит более умеренную оценку.

Или, можно разделить пользователей на более и менее критичных. Кто-то легко ставит высокие рейтинги, кто-то - наоборот.

Эти смещения (предубеждения) необходимо учитывать при прогнозировании.

Введем новые переменные:

  • \mu- среднее значение баллов, выставленных по всем items всеми users;

  • b_i - смещение, вносимое элементом;

  • b_u- предвзятость, внесенная пользователем;

Тогда, скорректированный прогноз (с учетом смещения) :

\hat{r}_{ui} = \mu + b_i + b_u + q^T_i p_u

В таком случае минимизируем следующий функционал:

\sum_{r_{ui} \in R_{train}} \left(r_{ui} - \mu + b_i + b_u + q^T_i p_u \right)^2 + \lambda\left(b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2\right) =\sum_{r_{ui} \in R_{train}} \left(r_{ui} - \hat{r}_{ui} \right)^2 + \lambda\left(b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2\right)

Оптимальное решение будем искать с помощью градиентного спуска.

Ошибку обозначим как e_{ui} = r_{ui} - \hat{r}_{ui}

Градиенты по b_u, b_i, p_u, q_i:

\nabla b_u = \left(r_{ui} - \mu + b_i + b_u + q^T_i p_u \right) - \lambda b_u = e_{ui} - \lambda b_u

\nabla b_i = e_{ui} - \lambda b_i

\nabla p_u = e_{ui} \cdot q_i - \lambda p_u

\nabla q_i = e_{ui} \cdot p_u - \lambda q_i

Тогда градиентный шаг выполняется по формулам:

b_u \leftarrow b_u + \gamma (e_{ui} - \lambda b_u)

b_i \leftarrow b_i + \gamma (e_{ui} - \lambda b_i)

p_u \leftarrow p_u + \gamma (e_{ui} \cdot q_i - \lambda p_u)

q_i \leftarrow q_i + \gamma (e_{ui} \cdot p_u - \lambda q_i)

где \gamma - коэффициент скорости обучения learning rate (гиперпараметр).

Реализуем алгоритм.

Данные возьмем из первой части статьи. 

import numpy as np
import pandas as pd
k = 10 # максимальная оценка

movies = ['Фантазия', 'ВАЛЛ-И', 'Пиноккио', 'Бемби' , 'Шрэк', 'Дамбо', 'Спасатели', 'Геркулес', 'Кунг-фу Панда']
m_movies = len(movies)

users = ['Андрей', 'Аня', 'Алиса', 'Ваня', 'Леша', 'Оксана', 'Саша', 'Паша', 'Сеня', 'Гриша']        
n_users = len(users)

Созданим рейтинги R_train случайным образом

np.random.seed(42)

N = np.random.randint(50, 60) # сколько оценок будет поставлено

ind_users, ind_movies, rating = [], [], []
user_movie = [] # чтобы пара user-movie не повторялись

for _ in range(N):
    user = np.random.randint(0, n_users)
    movie = np.random.randint(0, m_movies)
    if not [user, movie] in user_movie:
        ind_users.append(user)
        ind_movies.append(movie)
        rating.append(np.random.randint(1, k)) # случайная оценка пользователя фильму
        user_movie.append([user, movie])        
N = len(user_movie)

data = {'userId': ind_users, 'movieId': ind_movies, 'rating': rating}
R_train = pd.DataFrame(data = data)
R_train.head(3)

Посмотрим как выглядит User-item matrix

User_item_matrix = R_train.pivot(columns = 'movieId', index = 'userId', values = 'rating')
User_item_matrix.rename(columns = dict(zip(User_item_matrix.columns, movies)), inplace = True)
User_item_matrix.set_index(pd.Index(users), inplace=True)
User_item_matrix

Найдем среднее по всем рейтингам:

mu = R_train['rating'].mean()
mu

5.441860465116279

Инициализируем смещение, вносимое фильмами и "предвзятость" пользователей

bu = np.zeros(n_users)
bm = np.zeros(m_movies)
print(bu.shape, bm.shape)

(10,) (9,)

Инициализируем скрытые факторы пользователей и скрытые факторы фильмов

d = 5  # главных компонент
pu = np.random.normal(0, 0.1, (n_users, d))
qm = np.random.normal(0, 0.1, (m_movies, d))
print(pu.shape, qm.shape)

(10, 9) (9, 9)

Градиентный спуск

epoch = 5
gamma = 0.02
lmbda = 0.03

for _ in range(epoch):
    
    for index in range(R_train.shape[0]):

        user_id = R_train['userId'][index] 
        movie_id = R_train['movieId'][index] 
        rating = R_train['rating'][index]

        err = rating - (mu + bu[user_id] + bm[movie_id] + qm[movie_id] @ pu[user_id])

        bu[user_id] += gamma * (err - lmbda * bu[user_id]) 
        bm[movie_id] += gamma * (err - lmbda * bm[movie_id]) 
        pu[user_id] += gamma * (err * qm[movie_id] - lmbda * pu[user_id])
        qm[movie_id] += gamma * (err * pu[user_id] - lmbda * qm[movie_id])

Посчитаем предсказания для всех пользователей и фильмов:

R_pred = np.zeros((n_users, m_movies))

for user in range(n_users):
    for movie in range(m_movies):
        R_pred[user][movie] = round(mu + bu[user] + bm[movie] + qm[movie] @ pu[user], 2)

pd.DataFrame(R_pred, users, movies)

Можно воспользоваться библиотекой scikit-surprise.

from surprise import Reader, Dataset, SVD
from surprise.model_selection import train_test_split
from surprise import accuracy

# создание объекта класса Reader
reader = Reader(rating_scale=(1, 10))

# создание объекта класса Dataset
dataset = Dataset.load_from_df(R_train[['userId', 'movieId', 'rating']], reader)

# разбиение данных на обучающую и тестовую выборки
trainset, testset = train_test_split(dataset, test_size = 0.1)

# создание экземпляра класса SVD
model = SVD()

# обучение модели на обучающей выборке
model.fit(trainset)

# предсказание рейтингов на тестовой выборке
predictions = model.test(testset)

# оценка качества модели
print('RMSE:', accuracy.rmse(predictions))
print('MAE:', accuracy.mae(predictions))

R_pred_surprise = np.zeros((n_users, m_movies))
for u in range(n_users):
    for m in range(m_movies):
        R_pred_surprise[u][m] = model.predict(u, m).est
        
pd.DataFrame(np.round(R_pred_surprise, 2), users, movies)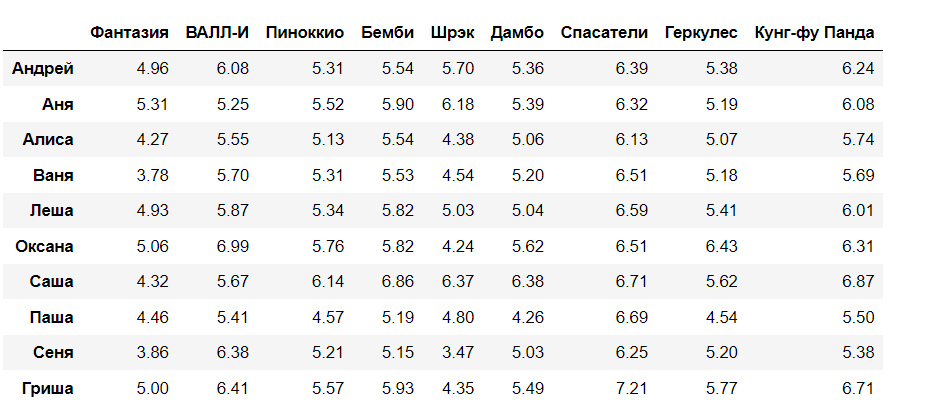

В конце соревнования Netflix выплатил миллион долларов победителям. Позже, организаторы конкурса признались, что за такую ничтожную сумму они не смогли бы заставить работать столько ученых по всему миру целых три года.

Однако, благодаря конкурсу, мы теперь знаем все о разложении user-item. Такие задачи принято называть 2D-задачи, потому что имеем данные о взаимодействии двух разных множеств.

Но мы можем учитывать, например, ситуативный контекст (если планируется семейный просмотр фильма - это один вид рекомендаций, если с друзьями - другой, если наедине - третий и тд), тогда мы можем говорить о больших размерностях для данной задачи. Современные рекомендательные системы уходят именно туда: как рекомендовать в условиях когда у нас много разнообразной разнородной дополнительной информации.

Комментарии (0)