Collaborative Filtering - подход, основанный на отношениях между пользователями (users) и товаром (items), при этом нет никакой информации о пользователях или товарах.
Взаимодействие между пользователем и товаром разделят на две категории:
Явное взаимодействие. Например, рейтинг, который пользователь ставит товару.
Неявное взаимодействие. Например, клик, просмотр или покупка товара не очевидны с точки зрения рейтинга.
User-item matrix — это таблица, в которой каждая строка представляет собой пользователя, каждый столбец - товар, а каждая ячейка содержит информацию о взаимодействии между пользователем и товаром. Например, в ячейке может быть указано количество раз, которое пользователь купил товар, или оценка, которую пользователь поставил товару. User-item matrix используется в рекомендательных системах для определения предпочтений пользователей и предложения им наиболее подходящих товаров. Очевидно, что user-item matrix - очень большая и разряженная матрица.

Для таких задач применяют матричную факторизацию (представление user-item matrix в виде произведения двух или более матриц более простого вида).
Часто матричная факторизация применяется для уменьшения размерности, где мы пытаемся уменьшить количество элементов, сохраняя при этом соответствующую информацию.
Так дело обстоит с основным компонентным анализом (PCA) и разложение по сингулярному значению (SVD).
где — user-item matrix,
— диагональная матрица с неотрицательными сингулярными числами,
и
— ортогональные матрицы и
.
PCA — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Вычисление главных компонент может быть сведено к вычислению SVD разложения матрицы данных или к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных.
Математическое содержание метода главных компонент — это SVD разложение ковариационной матрицы, то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств
, а самой матрицы
— в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами
.
Оставив -первых (главных) компонент (
) в SVD разложении, получим наиболее точное приближение к
по норме Фробениуса.
За "Скрытым текстом" пример использования SVD и PCA.
Hidden text
Наглядно как работает SVD и PCA.
import numpy as np
from matplotlib import image
from matplotlib import pyplot as plt
import cv2img = image.imread("photo.jpg")
plt.imshow(img)
plt.show()
Для работы с меньшей размерностью перейдем к черно-белому изображению.
gray_img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
plt.imshow(gray_img, cmap='gray')
plt.show()
gray_img.shape
(558, 563)Применим SVD разложение
U, lmbd, V = np.linalg.svd(gray_img)
U.shape, lmbd.shape, V.shape
((558, 558), (558,), (563, 563))S = np.zeros((U.shape[1], V.shape[0]))
S[ : U.shape[1], : U.shape[1]] = np.diag(lmbd)
S.shape
(558, 563)Вернем как было, убедимся что ничего не изменилось
plt.imshow(U @ S @ V, cmap='gray')
plt.show()
Попробуем оставить первые 100 компонент и посмотрим насколько изменится качество изображения.
d = 100
U_crop = U[:, :d]
S_crop = S[:d, :d]
V_crop = V[:d, :]
plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray')
plt.show()
Качество картинки почти не изменилось, зато сколько сэкономлено памяти!
Попробуем оставить первые 50 компонент.
d = 50
U_crop = U[:, :d]
S_crop = S[:d, :d]
V_crop = V[:d, :]
plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray')
plt.show()
Оставим первые 10 компонент.
d = 10
U_crop = U[:, :d]
S_crop = S[:d, :d]
V_crop = V[:d, :]
plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray')
plt.show()
Сингулярные числа в матрице S расположены по убыванию: чем ближе к началу, тем компоненты важнее и сильнее влияют на качество изображения.
Уберем первые 5 компонент.
k = 5U_crop = U[:, k:]
S_crop = S[k:, k:]
V_crop = V[k:, :]
plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray')
plt.show()
Качество картинки значительно хуже.
Представим нашу user-item matrix как произведение следующих матриц:
Тогда ‑aя строка
— это представление
‑го пользователя, а
‑ый столбец
— представленте
‑го товара. Их отношение (рейтинг) выражается с помощью скалярного произведения:
Матрицы и
найдем с помощью градиентного спуска.
В качестве возьмем
без регуляризации для простоты:
Посчитав градиенты по и по
, получим формулы обновления весов:
k пробегает от 1 до d, где d - число главных компонент.
Продемонстрируем работу алгоритма. Пусть нам заданы пользователи и их оценки к просмотренным фильмам. Задача - спрогнозировать незаполненные ячейки user-item matrix.
import numpy as np
import pandas as pdЗададим пользователей и фильмы:
k = 10 # максимальная оценка
movies = ['Фантазия', 'ВАЛЛ-И', 'Пиноккио', 'Бемби' , 'Шрэк', 'Дамбо', 'Спасатели', 'Геркулес', 'Кунг-фу Панда']
m_movies = len(movies)
users = ['Андрей', 'Аня', 'Алиса', 'Ваня', 'Леша', 'Оксана', 'Саша', 'Паша', 'Сеня', 'Гриша']
n_users = len(users)Оценки раскидаем случайным образом. С учетом чтобы пара user-movie не повторялась
RANDOMSEED = 42
np.random.seed(42)
N = np.random.randint(50, 60) # сколько оценок будет поставлено
ind_users, ind_movies, rating = [], [], []
user_movie = [] # чтобы пара user-movie не повторялись
for _ in range(N):
user = np.random.randint(0, n_users)
movie = np.random.randint(0, m_movies)
if not [user, movie] in user_movie:
ind_users.append(user)
ind_movies.append(movie)
rating.append(np.random.randint(1, k)) # случайная оценка пользователя фильму
user_movie.append([user, movie])
N = len(user_movie)
def get_user_item_matrix(n_users, m_movies, ind_users, ind_movies, rating):
R = [[0] * m_movies for _ in range(n_users)]
N = len(ind_users)
for i in range(N):
R[ind_users[i]][ind_movies[i]] = rating[i]
R = np.array(R)
return R
R = get_user_item_matrix(n_users, m_movies, ind_users, ind_movies, rating)
pd.DataFrame(R, users, movies) 
Ошибку будем считать как:
def MSE(R, U, V):
mse = 0
for ind in range(N):
i = ind_users[ind]
j = ind_movies[ind]
mse += ( R[i][j] - np.dot(U[i,:], V[:,j]) )**2 / N
return mseИспользовать будем стохастический градиентный спуск c фиксированным шагом step. Сделаем n_iters итераций.
def SVD(ind_users, ind_movies, R, d, step, n_iters):
# инициализация матриц разложения
P = np.random.rand(R.shape[0], d)
Q = np.random.rand(d, R.shape[1])
start_mse = MSE(R, P, Q)
# Стохастический градиентный спуск
for n in range(n_iters):
ind = np.random.randint(0, N)
i = ind_users[ind]
j = ind_movies[ind]
for k in range(0, d):
P[i, k] = P[i, k] + step * (R[i][j] - P[i, :] @ Q[:, j]) * Q[k, j]
Q[k, j] = Q[k, j] + step * (R[i][j] - P[i, :] @ Q[:, j]) * P[i, k]
mse = MSE(R, P, Q)
return P, Q, start_mse, mse
P, Q, start_mse, mse = SVD(ind_users, ind_movies, R, 3, 0.1, 3000) start_mse, mse
(22.327189007469947, 0.9592817343783187)Спрогнозируем user-item matrix
R_pred = np.zeros((R.shape[0], R.shape[1]))
for i in range(n_users):
for j in range(m_movies):
R_pred[i][j] = round(P[i,:] @ Q[:,j], 2)
pd.DataFrame(R_pred, users, movies)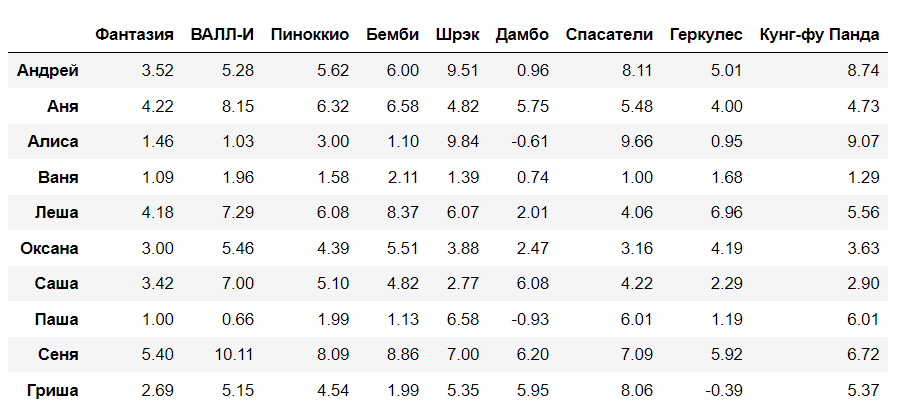
# Вывод еще раз для сравнения
pd.DataFrame(R, users, movies)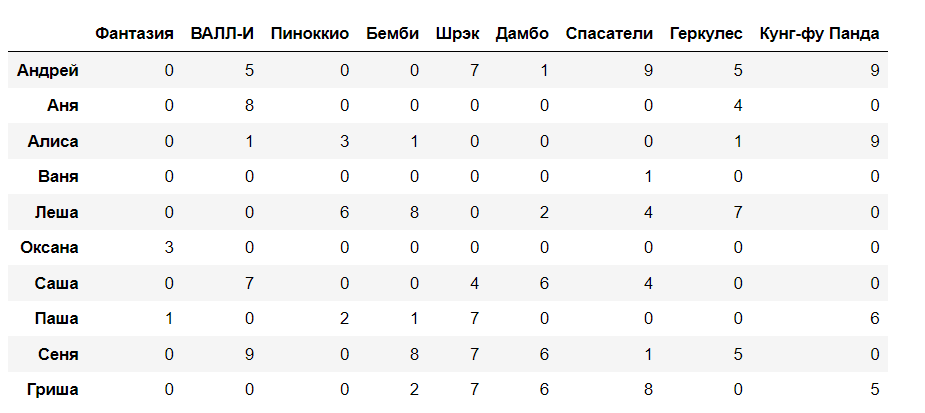
Комментарии (2)

vbogach
31.07.2023 10:57А есть какое-то обоснование, почему матрицы, найденные градиентным спуском эквивалентны матрицам, полученным алгоритмом PCA? Будут ли совпадать собственные значения/собственные векторы? Если матрица PCA является наилучшим приближением, то градиентный спуск до полной численной сходимости не будет эквивалентен PCA (поскольку на следующей итерации градиентного спуска приближение будет лучше текущего, следовательно, текущее приближение не является наилучшим, следовательно не эквивалентно PCA)?


bredd_owen
Большое спасибо! Не поверите, но я буквально за час до публикации Вашей статьи читал то же самое на https://machinelearningmastery.com/using-singular-value-decomposition-to-build-a-recommender-system/