Введение

Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.
Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.
Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.
Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.
Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:
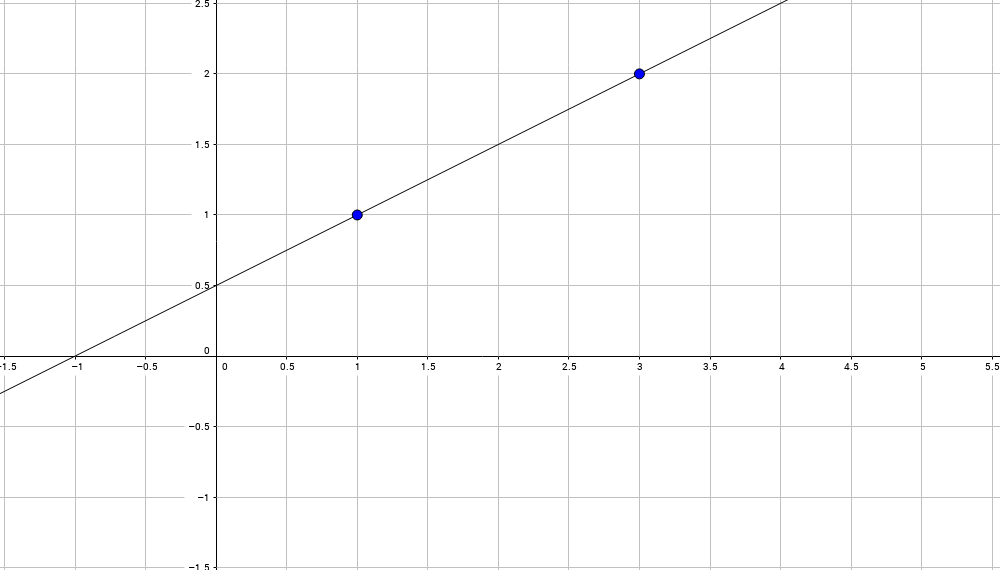
Эта прямая должна иметь уравнение типа следующего:
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
Можно записать это уравнение в матричном виде:
Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.
Давайте заменим конкретные матрицы на их символьное представление:
Тогда (alpha, beta) может быть легко найдено:
Более конкретно для наших предыдущих данных:
Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):
Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:
В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha\*i + beta\*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:
И будем стараться минимизировать эту ошибку:
Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.

Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:

Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:
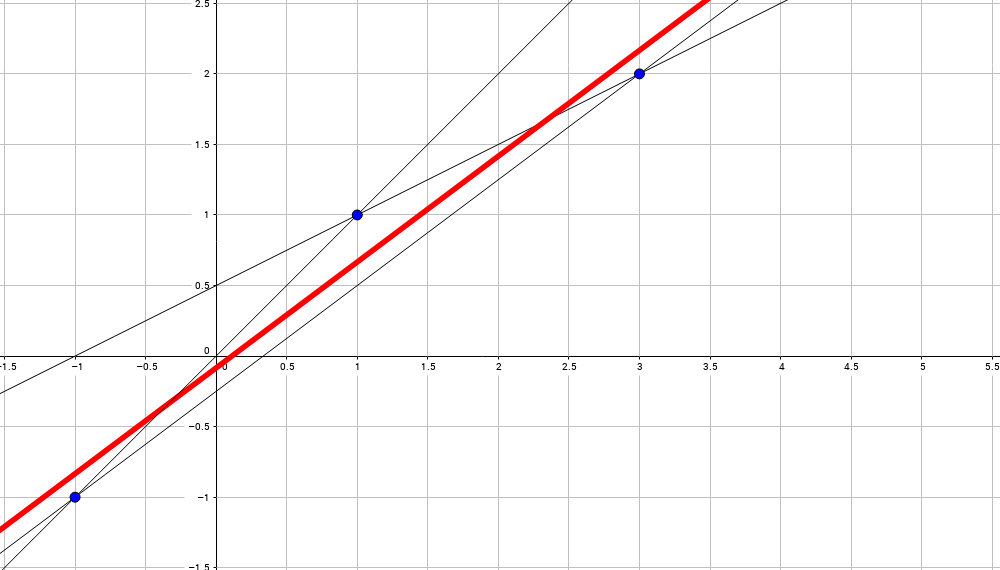
Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.
Минимум квадратичной формы
Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:
Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:
Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:
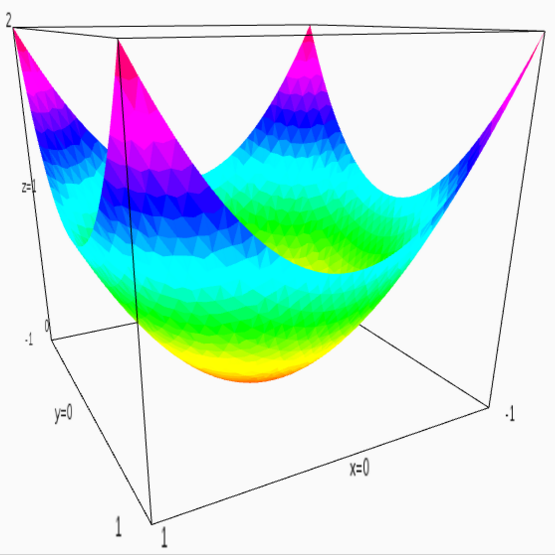
Вся эта гимнастика известна под именем линейной регрессии.
Уравнение Лапласа с граничным условием Дирихле
Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:

Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:
for (int d=0; d<3; d++) {
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, verts.size());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<(int)verts.size(); i++) {
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(verts[i][d]);
nlEnd(NL_ROW);
}
for (unsigned int i=0; i<faces.size(); i++) {
std::vector<int> &face = faces[i];
for (int j=0; j<3; j++) {
nlBegin(NL_ROW);
nlCoefficient(face[ j ], 1);
nlCoefficient(face[(j+1)%3], -1);
nlEnd(NL_ROW);
}
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
for (int i=0; i<(int)verts.size(); i++) {
verts[i][d] = nlGetVariable(i);
}
}
X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.
Все последующие строки матрицы A (faces.size()*3 = количеству рёбер всех треугольников в сетке) имеют одно вхождение 1 и одно вхождение -1, причём вектор b имеет нулевые компоненты напротив. Это значит, я вешаю пружинку на каждое ребро нашей треугольной сетки: все рёбра стараются получить одну и ту же вершину в качестве отправной и финальной точки.
Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.
Вот результат:

Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:
for (int i=0; i<(int)verts.size(); i++) {
float scale = border[i] ? 1000 : 1;
nlBegin(NL_ROW);
nlCoefficient(i, scale);
nlRightHandSide(scale*verts[i][d]);
nlEnd(NL_ROW);
}
В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:

Давайте вдвое усилим пружинки между вершинами:
nlCoefficient(face[ j ], 2);
nlCoefficient(face[(j+1)%3], -2);
Логично, что поверхность стала более гладкой:

А теперь ещё в сто раз сильнее:

Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.
Уравнение Пуассона
Давайте ещё крутое имя вспомним.
Предположим, что у меня есть такая картинка:

Всем хороша, только стул мне не нравится.
Разрежу картинку пополам:


И выделю руками стул:

Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:
for (int i=0; i<w*h; i++) {
if (m.get(i%w, i/w)[0]<128) continue;
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(a.get(i%w, i/w)[0]);
nlScaleRow(100);
nlEnd(NL_ROW);
}
for (int i=0; i<w-1; i++) {
for (int j=0; j<h-1; j++) {
for (int d=0; d<2; d++) {
nlBegin(NL_ROW);
int v1 = b.get(i, j )[0];
int v2 = b.get(i+d, j+1-d)[0];
nlCoefficient( i + j *w, 1);
nlCoefficient((i+d)+(j+1-d)*w, -1);
nlRightHandSide(v1-v2);
nlScaleRow(10);
nlEnd(NL_ROW);
}
}
}
Вот результат:

Код и картинки доступны здесь.
Пример из жизни
Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:
У меня есть некоторое количество фотографий образцов ткани типа вот такой:

Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:

Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:

Вот фрагмент, где чётко видно шов:

Поэтому я вырезать буду не по ровной линии, вот линия разреза:

А вот повторённый четыре раза паттерн:

И его фрагмент, чтобы было виднее:

Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:

Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.
Комментарии (367)

grigorym
23.02.2016 11:42+1У автора там в середине промелькнула картинка, где минимизировались расстояния от точек до искомой прямой по перпендикуляру. Это ошибка. В методе МНК минимизируются не расстояния по перпендикуляру, а разница между модельным значением и истинным значением при одном и том же иксе. Другими словами, минимизируются не красные отрезки, а зеленые:

splav_asv
23.02.2016 11:53Они отличаются умножением на константу, так что это то же самое.

grigorym
23.02.2016 12:06Минимизация F(p) = Sum (yi — f(xi, p))^2 -> min подразумевает именно зеленые линии.
khim
23.02.2016 14:02+1Это ни разу не "то же самое". Рассмотрите четыре точки в вершинах высокого и узкого прямоугольника. Минимизация красных линий дала бы вам вертикальную прямую, минимизация зелёных — даст горизонтальную. То же самое будет если вы возьмёте не одну точку, а "рой" точек.
Проблема в том, что ваша "константа" зависит от угла наклона прямой! Вот для уравнения "y = x + ?" (при неизменном наклоне прямой) это действительно неважно — но в статье-то речь не об этом!

Mrrl
23.02.2016 14:05"Константа" зависит от угла наклона прямой. В случае минимизации зелёных линий оптимальная прямая будет иметь несколько меньший угол наклона, чем в случае минимизации красных. Так что это не то же самое.

Keroro
25.02.2016 09:00+2Завис на фразе "Можно записать это уравнение в матричном виде", пока не вспомнил правило перемножения матриц. Как-то не вполне вяжется со следующей фразой: "Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит.". Значит всё таки не только способ записи, но и определённые законы? И как определить, когда "можно записать в матричном виде", а когда — нельзя?

haqreu
25.02.2016 12:08Ох. Зависит. Для меня лично никаких операций над двумерным массивом делать нельзя, пока вы не вложили смысл в то, что в нём хранится. Например, весьма распространено выражать точки через вектор-столбцы. Казалось бы, в общем и целом сложение может быть определено для матриц. А вот для точек сложение не определено. Таким образом, лично я считаю, что первично определить, что за объект мы храним в двумерном массиве, а затем уже говорить про операции.

MichaelBorisov
25.02.2016 23:34"Линейно-квадратичный регулятор" — к сожалению, это заимствованный термин, вытеснивший наш родной, русский. ТОУ ведь во многим обязана русским ученым, таким как Л.С. Понтрягин.
В русской школе ТОУ эта штука называлась "Аналитическое конструирование регуляторов".
Ну а если на пальцах — то упомянутый регулятор — это по сути тот же ПИД, но только с оптимально рассчитанными коэффициентами. Ну и немного в более общем виде — это такой регулятор, выходные функции которого являются линейной комбинацией переменных состояния, и метод их конструирования в сущности занимается расчетом коэффициентов этой линейной комбинации. В одномерном случае u=k*(x-x0), где u — управляющее воздействие, k — неизвестный коэффициент, x — измеряемая переменная состояния, x0 — ее желаемое значение.
haqreu
25.02.2016 23:38Не совсем согласен про (только) пид, но большое спасибо за справку. Не обессудьте, про Понтрягина, конечно, слышал, но обучаюсь по англоязычной литературе, отсюда кальки.


Temmokan
К слову, не поясните, в какой области наук вы учёный (научный работник)? Ну там, направление работы, публикации, чем вообще занимаетесь. Из праздного любопытства.
Поскольку вброс ваш про квадратные уравнения вызвал достаточно продолжительную реакцию. Хотя, если подумать, людям, далёким от математики и точных наук большинство премудростей в жизни нафиг не нужны.
Не нужны им ни квадратные уравнения, ни все эти Ферма с их теоремами. Ни начала термодинамики, ни физхимия, ни идеальные газы, ни излучение Хокинга. Про таблицу Менделеева простой человек вспомнит только в связи с расхожей фразой "в [название продукта] сплошь химия!"
В общем-то, понятно, что квадратные уравнения ценны как этап в постижении математики, не сами по себе. Человеку обычному науки не нужны. Всё, что нужно, ему донесут из СМИ всех родов, и из общения с другими простыми людьми. И это вроде как нормально — поскольку, на самом деле, "на пальцах" (т.е., для полного невежды) ничего не объяснить. Без знания аксиоматики в математику не въехать, как и без знания английского не оценить красоту сонетов Шекспира в оригинале. Минимум знаний нужен всегда, ex nihili nihil fit, простите мою латынь.
Я, кстати видел реакцию человека девственного в смысле познаний в математике, на демонстрацию листа Мёбиуса. Так это был реальный шок — и осознание односторонности, и последствия разрезания по середине листа, и не по середине. Так что математика и рассудку повредить может, если упадёт на неподготовленный рассудок.
Пусть уже всем этим занимаются специально обученные люди. Всерьёз, в смысле. А популяризация — дело нужно, как минимум — чтобы заинтересовать потенциальных новых учёных. Которые научные работники.
rocknrollnerd
Слушайте, но это же не вброс, серьезно) Автор просто говорит, что это такой метод познания, условно говоря — сделать глупое лицо и сказать "я не понимаю, зачем это нужно", чтобы потом получить простой пример — и понять) Нигде же не было фразы "квадратные уравнения не нужны, давайте жечь учебники и выть на луну".
То есть среднестатистический школьник на уроке о квадратных уравнениях должен иметь возможность поднять руку, встать и честно заявить "я не понимаю, зачем эти штуки мне нужны, объясните, пожалуйста?". После чего преподаватель рассказывает ему о компьютерной графике, у школьника загораются глаза, и вернувшись домой, он закапывается в книжки и добирается до линейной алгебры
и пишет свой OpenGL. Сейчас школы так не делают, и это плохо, по-моему — в результате, когда среднестатистические школьники потом становятся среднестатистическими родителями, у них вечные проблемы с ответом на вопрос "а зачем моим детям вообще учить математику?", на который они отвечают что-то в духе "ну, чтобы мозги упражнять".И все то же самое применимо к взрослым людям и чуть более замороченной математике. Вот читал я статью вчера, и не мог понять — нафига мне нужен minimum description length principle? Но я нашел более простую статью и все понял)
Temmokan
Вброс это провокационное заявление (необязательно в негативном смысле). Подтверждение — приведённая ниже цитата из OP:
Что это, как не вброс? (вопрос риторический)
haqreu
Да, большое спасибо. Мои студенты избегают математики как огня именно потому, что им в принципе не объясняли, что это всё полезно. Моё основное утверждение состоит в том, что при обучении школьников и студентов всегда можно привести вполне говорящий пример, зачем это всё нужно. Лично я окончил матмех СПбГУ, отделение чистая математика. Да, меня обучали топологии, только за пять лет мне не привели ни единого примера, зачем нужна топология. Зачем вон те самые когомологии, о которых спросили выше. А ведь они очень даже нужны, чтобы 3Д модели текстурировать, и объясняется там всё куда как прозаичнее и понятнее, нежели на приведённой выше ссылке.
Именно поэтому я стараюсь никогда не читать лекции из разряда: "Ну это же фундаментально! Пригодится потом!" Нет. Градиент? Окей, градиентный спуск, минимизация усилий. Ковариации? Не вопрос, вот вам лабораторная по распознаванию звука. И тому подобное.
И читая школьные и вузовские учебники, у меня волосы дыбом встают, я вообще не понимаю, как я сам-то через это продрался. А мне было отчаянно скучно считать про две трубы в бассейне именно потому, что это просто лицемерно — давать словесное определение задачи, когда оно лишено житейского смысла. Давайте сразу уравнение, его и решим. Или приводите нормальные примеры.
rocknrollnerd
Я немного удивлен количеству людей в комментах, которые из вашей фразы сделали прямо противоположные выводы) В любом случае, пишите еще, и побольше таких преподавателей)
(напальцево-практический подход недавно очень порадовал вот в этом курсе на Курсере. Кому, казалось бы, легче от того, что функцию Бесселя можно увидеть, если покрутить свободным концом веревки? Мне, например, очень)
Arastas
Помню, что на первом курсе спросил — а зачем матрице детерминант. Мне сказали — "много зачем!" и я отстал.
haqreu
Очень показательный пример, спасибо.
Temmokan
В аналогичной ситуации я потребовал конкретных примеров. Получил (чтобы выяснить, не являются ли строки или столбцы линейно зависимыми; для решения системы линейных уравнений и т.д.).
От преподавателя зависит.
haqreu
Это равенство определителя нулю, весьма ограниченное применение. А ещё?
Temmokan
Чем, простите, ограниченное?
В моём комментарии упомянуто два использования детерминанта. Третье, навскидку — вычисление обратной матрицы.
haqreu
Из ваших слов мне кажется наиболее вероятным, что с определителями/собственными числами вы имели дело только на семинаре по линейной алгебре на первом курсе вуза. Почему мне так кажется?
Потому, что вы предлагаете проверить детерминант на строгое равенство нулю (линейная зависимость и остальные ваши применения, типа обратной матрицы). А что если он равен не нулю, а 1e-10? А если 1e10?
Именно поэтому мне кажется, что вы оперируете этими понятиями на уровне синтаксическом: вам определили алфавит и набор грамматических правил на нём. А картинки, которая объясняет что это такое в голове у вас нет. Применения вытекают только из того, чем объект является. А этого понимания, опять же, насколько я понимаю, у вас нет.
Temmokan
Громкие слова для человека, который называет себя учёным, но по великой скромности не хочет продемонстрировать хотя бы одну научную работу.
Есть у меня понимание или нет, простите, выясняется исключительно практическим путём — когда мне требуется решить задачу, в которой нужен детерминант. Или объяснить кому-нибудь, что это такое — в картинках и схемах, как нам в своё время объясняли.
Ноль — специальное значение детерминанта, при котором у его матрицы есть вполне конкретные свойства. Например, что у неё отсутствует обратная. "Почти ноль" или "совсем не ноль" — это все прочие случаи. Ничего, что я объясняю очевидное?
Надеюсь, что вы не скажете своим студентам "если у матрицы определитель ничтожно мал, можно считать, что обратной матрицы не существует".
haqreu
Голубчик, тема статьи и обсуждения — линейная алгебра, а не моя карьера. Не переходите на личности. Мне глубоко всё равно, что вы лично считаете меня болтуном и хвастуном, положение дел в обучении от этого не меняется.
Нет никаких специальных значений. Есть конкретные задачи, которые нужно решать, используя имеющийся инструментарий. Выбор инструментария обуславливается пониманием того, что из себя представляет каждый инструмент.
А в данном случае вы вообще забываете про стабильность численных вычислений. Видимо, просто потому, что это не входит в круг ваших интересов/занятий, а в вузе вам про это не рассказали.
Temmokan
"Врачу, исцелися сам".
Из чего следует, что я считаю вас болтуном и хвастуном? Вообще-то я просто считаю вас человеком, который научной работой не занимается, а занимается преподаванием. Заметьте: не употреблено ни единого уничижительного слова.
Не играйте в телепата, пожалуйста. Хотите знать, что дуамет собеседник — просто спросите.
Ноль для детерминанта — вполне специальное значение. При нём у матрицы вполне конкретные свойства, которых не наблюдается при других значениях.
Это утверждение не противоречит утверждению, о том, что ноль для определителя матрицы — специальное значение.
Трудно забывать о том, о чём и разговор-то не шёл.
haqreu
Здрасте приехали. Всю дорогу тут идёт речь о реальных применениях математики, а вы так и не сумели привести ни одного.
Temmokan
Посмотрите, на что я отвечал, когда речь зашла о том, "зачем матрице детерминант". Каким боком тут "реальное применение математики"?
Можно далеко не ходить. В своё время я занимался неэмпирическими квантовохимическими расчётами. Сейчас в т.ч. занимаюсь криптографическими алгоритмами. Во вполне практической области, ПО пишу.
Это подходит под "реальное применение математики"?
Если речь про использование математики, отличной от арифметики под управлением калькулятора, т.н. простыми людьми, то на эту тему я достаточно подробно высказался выше.
haqreu
Спасибо, конечно, но мне неинтересно знать, чем конкретно вы занимаетесь. Я вас об этом и не спрашивал, прошу заметить.
Именно на вопрос "зачем" и нельзя отвечать "если ноль, то матрица плохая, а если не ноль, то хорошая". Ваш ответ на вопрос "зачем" бесполезен.
Этот самый детерминант (вкупе с другими критериями) и определяет, что такое плохая. В том числе и порядок, не просто "А плохая, Б плохая". А ещё и отношение "А лучше Б".
Temmokan
То есть ответа, подходит ли упомянутое мной использование математики под "реальное применение математики", не будет?
Абстрагируйтесь от меня и ответьте тогда на вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики?
Товарищ выше уже упомянул: вы выносите суждения с формальной, строгой части (где чётко определяется, что такое определитель, каковы его свойства и пр.) с точки зрения прикладного применения. Что попросту лишено смысла.
FransuaMaryDelone
Подрабатывал я в студенчестве вахтером в общежитии и вот как-то ночью спускается ко мне на вахту студент-первокурсник и заводит разговор. Сначала про методы наименьших квадратов, потом уравнение Пуассона, матрицы и определители пошли в ход, а потом предложил мне выбрать: горчицей или кетчупом проголосовать за американского президента. Да так разошелся, что на шум люди набежали. Ну скрутили, дурку вызвали. Переутомился парень — сессия.
haqreu
К теме обсуждения (определитель, а более глобально преподавание абстракций) ваша карьера относится так же, как если бы я заявил, что могу проплыть триста метров баттерфляем.
С вами я дискуссию закрою, у меня нет больше времени. Для тех, кто прочитает: вся статья про то, что самой по себе абстрактной математики, без наглядных иллюстраций, в школе быть не должно.
А определитель — это мера того, насколько линейное отображение далеко от единичного. Отсюда вытекают применения.
Temmokan
При чём тут моя карьера, а?
Повторяю свой вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики? — Заметьте, никакой привязки ни к чьей карьере.
У вас привычка уклоняться от ответов, когда ничто не мешает их дать. Боитесь показать, что вы, как и все люди, можете ошибаться? Или ещё каким-то образом повредить свой нимб?
Впрочем, уже неважно, картина вполне понятна, спасибо. "Садитесь, два".
haqreu
Слушайте, у меня действительно мало времени с вами флейм разводить, мне куда как полезнее ответить на вопросы рецензентов по моей монографии, но вы настолько неумело троллите, что я вас всё же покормлю.
Я не знаю, относится ся ли использование программы или даже пусть её написание к реальному применению математики. Может да, а может и нет, мне не хватает данных, чтобы ответить на этот вопрос.
Только я даже отвечать на него не хочу, так как к теме обсуждения, напоминаю, определитель, а более глобально преподавание абстракций, это не относится никаким боком.
Temmokan
Это кто недавно просил не переходить на личности?
Я и не начинал ещё вас троллить, если что. Нет смысла — вы сами по каждому моменту сливаетесь в полный рост. Даже скучно как-то.
Ну наконец-то.
Нет чтобы сразу ответить, чесслово.
haqreu
Ну я ответил, что не знаю, относится ли ваша работа к практическому применению математики, дальше-то какой вы вывод делаете? :)
Temmokan
Делаю вывод, что не знаете. По вашим же словам, недостаточно информации.
haqreu
Голубчик, ну не томите же, не томите! Скажите, зачем вам нужно было знать, могу ли я классифицировать вашу деятельность? Только очень вас прошу, пишите мысли полностью, а не кусочками!
На всякий случай напоминаю тему дискуссии.
Temmokan
Томитесь в неведении — то, что мне было нужно, я узнал. А потому не отвлекаю вас более от важных дел.
haqreu
Слив засчитан.
Temmokan
Ваши студенты правда читают этот тред? Тогда непонятно, кому слив засчитан на самом деле. :) Будем здоровы!
haqreu
Безусловно, наикрепчайшего вам здоровья! И за моих студентов и меня вы не беспокойтесь, всё будет отлично.
Мне только очень жаль, что ни одной полной мысли вы так нигде и не оформили. В итоге флейма вагон, а вынести (например, мне) из беседы нечего.
Temmokan
Это не более, чем ваше мнение. Ну не обязан я формулировать всё исключительно в доступной именно для вас форме.
Но, раз тут я говорю ни много ни мало с преподавателем, добавлю немного за химию и математику.
Мне повезло с преподавателями (по химии, физике, математике). Ещё со школы попадались люди, которые умели так всё изложить, что хотелось узнать больше. Имена, если кому интересно, я назову.
Плюс книги (полагаю, все, кто любит математику, знают имена Бориса Кордемского, Щепана Еланьского, Мартина Гарднера, Сергея Боброва, и других популяризаторов).
Одна общая у них черта: они никогда не принижают собственный предмет, даже в шутку. От них услышать что-нибудь вроде
было абсолютно невозможно. За что их и уважаю.
Кстати, книги упомянутых полезно читать и перечитывать студентам, которые боятся математики.
haqreu
Неужели вы так и не поняли, что конкретно к математике у меня нет ни малейшей претензии? У меня есть очень большие претензии к тому, как она используется. Математик — слово мистическое для большинства аудитории. Им быть престижно, потому что большинство аудитории совсем не понимает, чем этот самый математик занимается. И это порочный круг, это плодит всё больше и больше недобросовестности, утапливая понимание в океане умных слов. Гарднер безусловный молодец. И теорема Ферма нужна, и квадратные уравнения. Только не в том формате, который в данный момент широчайшим образом используется в школе и в вузах. Если лично вам повезло с преподавателями — это прекрасно. Только вы сами использовали слово повезло. А везти не должно, это должно быть систематическим результатом.
Temmokan
Скажите, в приведённых выше цитатах слово "математика" вы используете в одном и том же смысле?
Вы всегда выбирали преподавателя сами, находя лучшего из имеющихся? Заведомо зная, что он научит именно тому, что вам нужно?
Поделитесь умением, мэтр.
haqreu
Нет. В одном случае я говорю про науку, которую безмерно уважаю, в другом про то, как она выглядит для обывателя и как она используется недобросовестными (зачастую неосознанно недобросовестными) людьми для своего личного карьерного роста.
Разумеется, нет. Я ел то, что давали. И зачастую давали пищевой наполнитель, а не еду. И весь мой дискурс ровно о том, что это ненормальная ситуация, что нужно её исправлять.
Пожалуйста, вздохните глубоко, и перечитайте ещё раз всё, что тут написано. Вы боретесь с тем, что вы же сами и придумали. Не ищите в моих словах того, чего там нет. Ну и чуточку больше уважения к собеседнику тоже не помешает: несмотря на вашу упёртость и прямо скажем, не очень вежливые заявления, я стараюсь аккуратно до вас доносить свою мысль. Не всегда получается, иногда меня тоже заносит, но я стараюсь. Постарйтесь и вы, пожалуйста.
Temmokan
Тогда как понимать вот это -
в ответ на фразу "повезло с преподавателями"?
(вопрос риторический, если что)
"Врачу, исцелися сам".
Нелепо давать добрые советы дважды, но что поделать.
haqreu
Мне казалось, что я предельно ясно написал, давайте другими словами: я считаю, что в данный момент отрасль больна. Что преподавательская масса должна улучшиться, чтобы не нужно было везения для получения качественного образования.
Это включает в себя не только школу и вуз, это включает в себя и научные публикации, которые пишутся языком, доступным лишь узкому кругу посвящённых. Причём зачастую ещё и настолько, что этот узкий круг посвящённых сам себя и рецензирует, поднимая свой личный карьерный индекс, при этом допуская в своих работах невоспроизводимые, а то и просто ложные результаты.
Ну вот пожалуйста, непосредственно после просьбы не хамить вы опять за своё. Зачем?
Temmokan
Увы, не поспоришь. тут согласие по всем практически пунктам. Однако я говорил, во всех своих комментариях, о математике как о науке — и добросовестных учёных.
Возможно, следует уточнять контекст, прежде чем набрасываться с резкими высказываниями.
Я могу задать вам тот же вопрос.
К слову о позитивном: кого вы можете посоветовать как добросовестного математика-популяризатора нашего времени?
haqreu
Прошу заметить, что это вы не уточнили контекст и ринулись в бой с миражом, накручивая себя сильнее и сильнее, с первых же комментариев требуя подтверждения моей карьеры и прочего.
Раз уж мы закрываем весь этот флейм, и если вам всё ещё интересно, можете полистать мою монографию, которую я написал для получения хабилитации. К непосредственно текстам моих статей, подозреваю, у вас не будет доступа, т.к. журналы их продают. К слову сказать, вся эта информация вполне доступна, мои полные данные висят прямо у меня в профайле, не здесь, так на гитхабе.
К сожалению, не знаю. И буду крайне благодарен за любые ссылки. Могу привести вот этот комикс, его автор молодец.
Temmokan
Договорились, спасибо за ссылки.
FransuaMaryDelone
Mrrl
Что-то здесь не то. "Мера того, насколько линейное отображение далеко от единичного" — это какая-нибудь норма матрицы A-E, например, используется при ответе на вопрос "насколько точно мы определили ориентацию камеры". Определитель, если применять его к отображениям — объём параллелепипеда, являющегося образом единичного куба. Ничего общего.
haqreu
Не совсем ничего общего. Если этот объём сильно меньше объёма изначального куба, то есть немаленькая вероятность получить очень плохую обусловленность. Самого определителя для этого не хватает, я согласен, потому я выше и писал, что вкупе с другими критериями, такими как след и тп.
haqreu
А, я понял. Это я дебил, у меня профессиональная деформация, мне настолько много нужно считать всякое, не зависящее от вращений, что у меня в мозгу любое вращение — это единичное преобразование :)
splav_asv
Вы подходите с позиции строгой математики. Вам аппонент — с позиции прикладного применения и реальных расчётов. Если СЛАУ плохо обусловлена — с практической точки зрения, по факту, это так же плохо, как если бы определитель был нулём.
Temmokan
Согласен.
В таких случаях нужно начинать разговор с того, что определять контекст: "а если мы говорим про..." — и далее станет ясно, при чём тут очень малое значение детерминанта. После этого и поводов для спора не будет.
haqreu
Кстати, само по себе малое значение детерминанта ничего говорит про обусловленность системы.
haqreu
Я не совсем согласен с самим существованием "позиции строгой математики". Математика не существует сама по себе, она существует потому что нужно лечить людей и строить дома. И вполне себе строгая математика используется для оценки погрешности вычислений...
Temmokan
Т.е. все эти доказательства Великой Теоремы Ферма, поиски закономерности в простых числах, все эти числа Грэма и т.д. и т.п. нафиг не нужны человечеству?
haqreu
Гражданин, если вы не видите практической пользы в поисках закономерностей в простых числах, то это лично ваши пробелы в образовании. Закономерности ищут не для поиска закономерностей, а для решения конкретных прикладных задач. Не надо мистифицировать науку, а?
Temmokan
Я-то как раз вижу, о чём и писал. Прекращайте уже приписывать собеседнику чёрт-те что, если по существу вам нечего сказать.
Для вашей эрудиции: как побочный продукт, из вроде бы чисто умозрительного поиска закономерностей в простых числах, мы сейчас имеет системы шифрования с открытым ключом. Очень даже практическое, вполне востребованное применение. Это к слову о пользе фундаментальной науки.
Sapienti sat.
haqreu
Спасибо, я в курсе этого "побочного" продукта. И я очень даже за существование фундаментальной науки. Вы сказать-то что хотели? Попробуйте выдать полностью вашу мысль в формате: "Моё основное утверждение состоит в том: xxx".
Mrrl
К применениям равенства определителя нулю ещё можно добавить поиск собственных значений (откуда следует много дальнейших применений), проверка наличия кратных корней многочлена или общих корней двух многочленов… Из применений самого значения детерминанта сходу вспоминаются только вычисление ориентации базиса и якобиан системы функций — для замены переменных в кратных интегралах.
Но важнее то, что из-за нескольких свойств (полилинейность, антисимметричность, мультипликативность) с детерминантом очень удобно работать. Когда что-нибудь хорошо выражается, скажем, через перманент (например, число возможных паросочетаний), мы отмечаем это, как курьёзный факт, и ищем другие подходы.
Arastas
Я к тому моменту уже представлял и обратные матрицы, и всё такое базовое. Так что этот ответ меня бы совершенно не устроил.
Меня больше интересовало, как так вышло, что хитрым образом вычисляемый скаляр вдруг оказывается таким важным для матриц, в чём тут глубинный смысл. К сожалению, на такие вопросы ответить, вроде как, сложнее, чем на "где используется".
haqreu
Давайте я вам расскажу, как работает общение в человеческом обществе именно на этом примере. Вот вы читаете текст, увидели слово, которое вам не нравится, в данном случае "учёный". Тут есть два варианта развития событий:
1) Вы пишете: "Вам не кажется, что это слово звучит довольно помпезно?" На это вы получаете от меня ответ: "Хм, действительно. Прошу прощения, никогда не доводилось говорить о моей работе на русском языке, вот и промахи в терминологии. Ни в коем случае не собирался ставить себя в один ряд с фигурами калибра Ладау."
2) Вы пишете про учёных собак и требуете список публикаций. На что получаете предложение прогуляться.
Конкретно вы выбираете скорее второй путь. А первый куда как продуктивнее. И не раздражён никто, и текст поправлен, один профит. Список моих публикаций находится в гугле за пару минут максимум, вы даже этого не попытались сделать, только начали громогласно его требовать прямо вот сюда.
В общем, проходите, гражданин, не засоряйте эфир.
Temmokan
Это вы решили, что оно мне не нравится? Логично бы меня спрашивать, а не делать за меня выводы, верно?
Про учёных собак писал не я — это раз. Требовать я не требовал — это два. Поинтересовался, ведёте ли вы научную работу — в смысле, являетесь ли научным работником. Где вы там рассмотрели требование?
Достаточно было просто ответить "нет, не являюсь".
Пока что могу сделать вывод, что вы научной деятельностью не занимаетесь, только преподаванием. Верно?
haqreu
Из того, что вы-таки меня поправляете с этими научными работниками, я и делаю вывод, что слово учёный из моих уст вам не нравится. Я ошибся?
Про чистое преподавание неверно.
Temmokan
Иными словами, "я учёной деятельностью занимаюсь, но подтверждать это не обязан". Без проблем.
Снимаю шляпу перед вашей скромностью. Ну и уступаю вам право, из нас двоих, засорять в этом треде эфир монопольно. :) Просто читать тоже весьма доставляет.
haqreu
Любезный, вы меня на слабо взять пытаетесь, что ли? :)
Temmokan
Я бы ответил вам, но ведь обещал не засорять эфир. Томитесь в неведении.
FransuaMaryDelone
Temmokan
Не смею претендовать на лавры Ландау, хотя звучит лестно.