Применение машинного обучения может включать работу с данными, тонкую настройку уже обученного алгоритма и т. д. Но масштабная математическая подготовка нужна и на более раннем этапе: когда вы только выбираете модель для дальнейшего использования. Можно выбирать «вручную», применяя разные модели, а можно и этот процесс попробовать автоматизировать.
Под катом — лекция ведущего научного сотрудника РАН, доктора наук и главного редактора журнала «Машинное обучение и анализ данных» Вадима Стрижова, а также большинство слайдов.
Мы поговорим о способах порождения и выбора моделей на примере временных рядов интернета вещей.
Концепция интернета вещей появилась уже более десяти лет назад. От обычного интернета он отличается прежде всего тем, что запрос делает не человек, а устройство или сообщение в сети, которое взаимодействует с другими устройствами без человека.
Пример первый. Никому не хочется каждый месяц лезть в угол с фонариком, смотреть, сколько намотал счетчик электроэнергии, и потом идти ногами платить. Понятно, что современные счетчики мониторят не только почасовое потребление энергии в квартире, но даже знают, сколько из каждой розетки ушло энергии.
Второй вариант. Мониторинг здоровья человека. Примерном временных рядов, которые находятся в этой области, является следующее. Сейчас больным тетраплегией, у которых отказали конечности, ставят прямо на кортекс датчик размером с ладошку. Его не видно изнутри, он полностью закрыт. Он даёт 124 канала с поверхности кортекса с частотой 900 герц. По этим временным рядам мы можем прогнозировать движение конечностей, то, как он хочет двигаться.
Следующий пример — торговля. Сейчас кассиры на выходе из магазина стоят дорого, и очередь на выходе из магазина — это тоже не есть хорошо. Требуется создать такую систему и получить такие сигналы, когда человек с тележкой, проезжая мимо выхода, получает сразу все значения цен купленных им продуктов.
Последний довольно очевидный пример — автоматическое регулирование работы городских служб: светофоров, освещения, датчиков погоды, наводнений и т. д.

Вот первый пример временных рядов, с которыми мы будем работать. У нас есть почасовое потребление электроэнергии, максимальная и минимальная суточная температура, влажность, ветер, длина светового дня.

Второй пример временных рядов, который иерархически находятся над первым, — то же самое, только для каждой точки некоторого региона. В данном случае показан кусочек Европы, и вместе с этими временными рядами, в частности, в каждой точке снимается значение загрязнения воздуха.

Ещё более сложный пример — значения электрического поля. По оси ординат отложены частоты, по оси абсцисс — время. Это тоже временной ряд. Если прошлый временной ряд — декартово произведение времени на пространство на пространство, то здесь мы имемм декартово произведение времени на частоты.
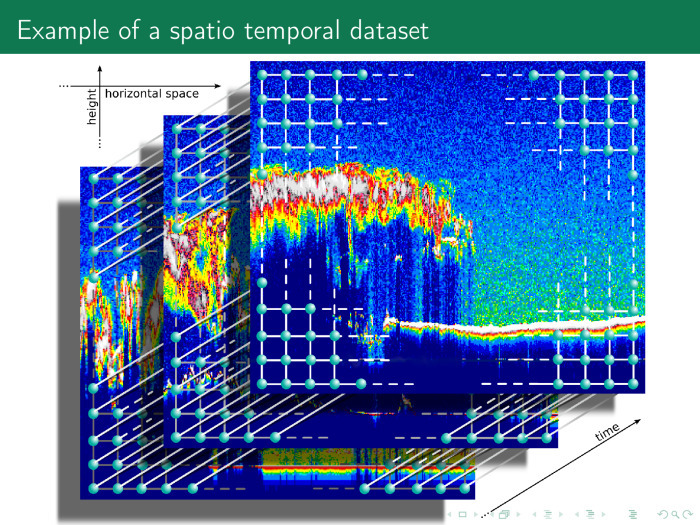
Следующий временной ряд ещё более сложный. По оси абсцисс и ординат пространство, по оси аппликат — время. Таким образом, у нас есть много разных красивых временных рядов, и временной ряд необязательно содержит только время и значения. Он может содержать декартово произведение нескольких осей времен, частот, пространств и т. д.
Рассмотрим самый простой вариант. У нас есть временные ряды потребления электроэнергии небольшого города. Есть цена, объем потребления, длина светового дня, температура и т. д. Эти временные ряды периодичны. Потребление электроэнергии колеблется в течение года, в течение недели и в течение суток.
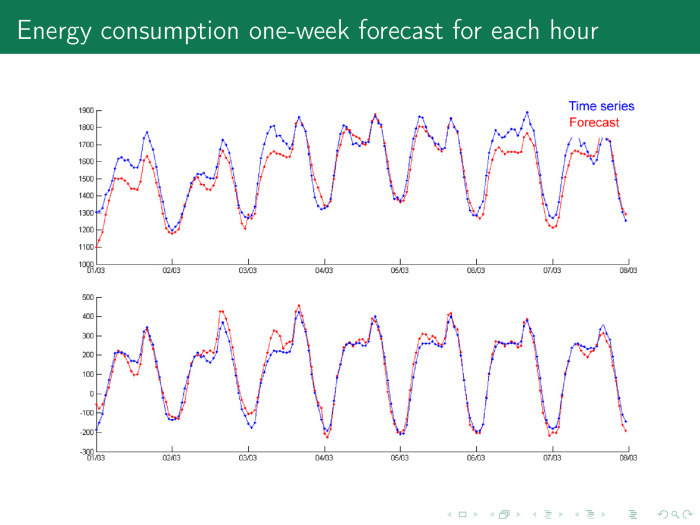
Возьмем произвольный день. Синий — временные ряды, красный — прогноз. 12 часов ночи, граждане засыпают, просыпается мафия. Временной ряд падает, потребление падает. Вся Москва ночью горит огнями, в общем-то, потому, что она окружена ТЭЦ, энергию девать некуда, и цена на электроэнергию может даже упасть ниже нуля, можно и доплачивать за электроэнергию — лишь бы потребляли.
6 часов, граждане просыпаются, едут на работу, пьют чай, потом работают, потом едут домой — этот цикл повторяется.
Задача — спрогнозировать по часам потребление электроэнергии на следующий день и закупить сразу всю электроэнергию на сутки. Иначе на следующий день придется доплачивать за разницу в потреблении, а это уже дороже.
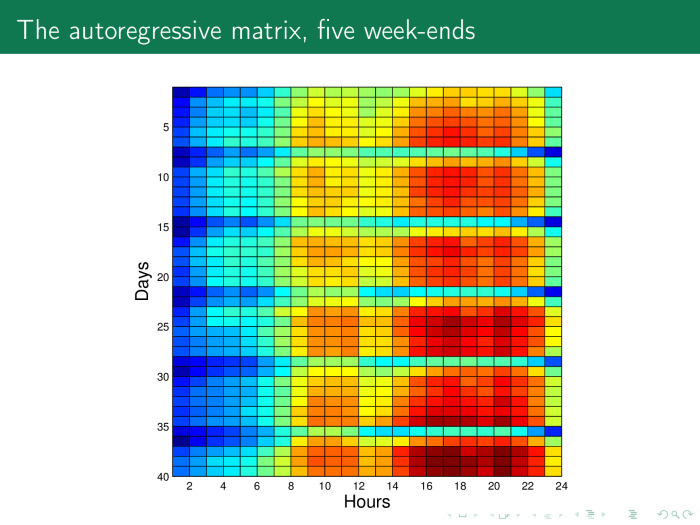
Каким образом решается такая задача? Давайте на основе предыдущего временного ряда построим такую матрицу. Здесь по строкам расположены дни, примерно 40 дней по 24 часа. И мы легко можем увидеть здесь особые строчки — субботы и воскресенья. Видно, что в Анкаре — так же, как и в Москве, — в субботу люди ведут себя довольно активно, а в воскресенье отдыхают.
Каждый столбец — в данном случае 20 часов какого-то дня недели. Всего здесь пять недель.

Представим эту матрицу в формальном виде. Мы берем временной ряд за хвостик, по дням недели или по неделям сворачиваем, получаем матрицу объект–признак, где объект — день, а признак — час, и решаем стандартную задачу линейной регрессии.
С помощью этого значения мы ищем, например, 12 часов следующего дня. То, что мы прогнозируем, мы считаем y за всю нашу историю. Х — вся история, кроме этих 12 часов. Прогноз — скалярное произведение последней недели, векторы значений и наших весов, которые мы получаем, например, с помощью метода наименьших квадратов.
Что надо сделать, чтобы получить более точный прогноз? Давайте породим различные элементы модели. Мы их называем порождающими функциями или примитивами.

Можно с временным рядом сделать следующее: взять из него корень. Можно его оставить, можно взять временной ряд – корень из временного ряда, временной ряд – логарифм из временного ряда и т. п.
Таким образом, мы добавляем столбцы к матрице объект–признак, увеличиваем число столбцов, а число строк остается прежним.
Более того, для порождения признаков мы можем использовать полином Колмогорова-Габора. Первый член — сами временные ряды. Второй член — все произведения временных рядов. Третий — произведение троек временных рядов. И так далее, пока нам не надоест.
Коэффициент собираем со всего временного ряда — и опять получаем линейную модель. После этого получаем довольно приличный прогноз. И даже возникает подозрение, не переобучились ли мы, не слишком ли хорош прогноз?
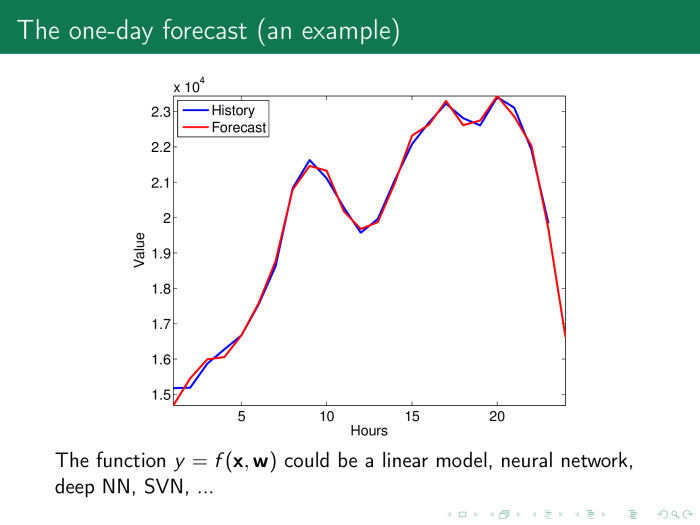
Он астолько хорош, что параметры вообще потеряли свой смысл.
Предположим, строка матриц плана — это неделя, 7 дней, 168 часов. Есть данные, например, за три года. В году 52 недели. Тогда базовая матрица за три года — это 156 строк на 168 столбцов.

Если мы используем шесть временных рядов, которые я перечислю, — то есть вместе с потреблением ещё учтём цену, влажность, температуру и так далее, — то столбцов в матрице станет уже более 1000. А если будет ещё четыре порождающих функции, то это 4000 строк и 156 столбцов. То есть матрица сильно вырождена, и нормально решить линейное уравнение не представляется возможным. Что же делать?
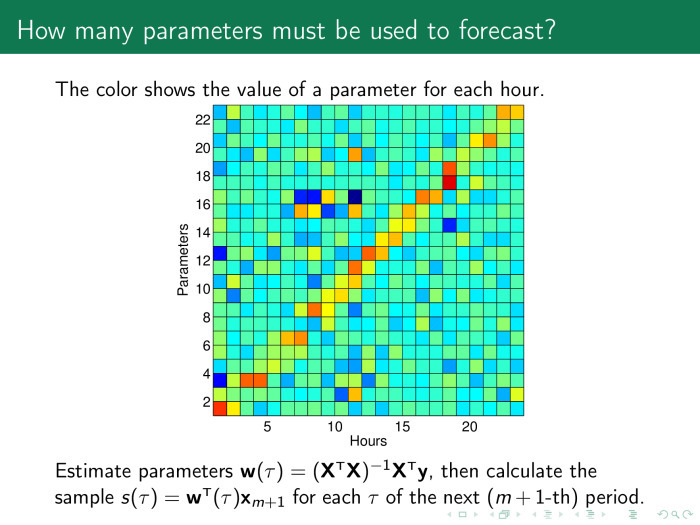
Наверное, надо запустить процедуру выбора моделей. Для этого надо посмотреть, какие веса имеют смысл. На каждый час мы строим свою модель, и здесь по оси абсцисс показаны значения параметров модели по часам на следующие сутки. А по оси ординат стоят сами параметры. Мы видим желто-красную диагональ, значение весов побольше там, где есть свой час в модели за предыдущие дни.
Принцип простой. Прогноз на завтра на 12 часов зависит от значений за 12 часов предыдущего дня, позавчерашнего и т. п. Таким образом, мы можем оставить только эти значения, а всё остальное выбросить.

Что именно надо выбрасывать? Представим матрицу х как набор столбцов. Мы приближаем временной ряд y линейной — или необязательно линейной — комбинацией столбцов матрицы х. Нам хотелось бы найти такой столбец ?, который был бы поближе к y. Значительная часть алгоритмов выбора признаков выберет нам столбцы ?1 и ?2, если мы захотим оставить два столбца. Но среди тех, что мы породили, нам нужны ?3 и ?4. Они дают одновременно точную и устойчивую модель. Точную — потому что линейная комбинация?3 и ?4 в точности приближает y, а устойчивую — потому что они ортогональны.
Почему именно два столбца? Надо посмотреть, в каком пространстве мы работаем, сколько объектов в нарисованной выборке. Здесь три объекта. Матрица х содержит 3 строки и 6 столбцов.
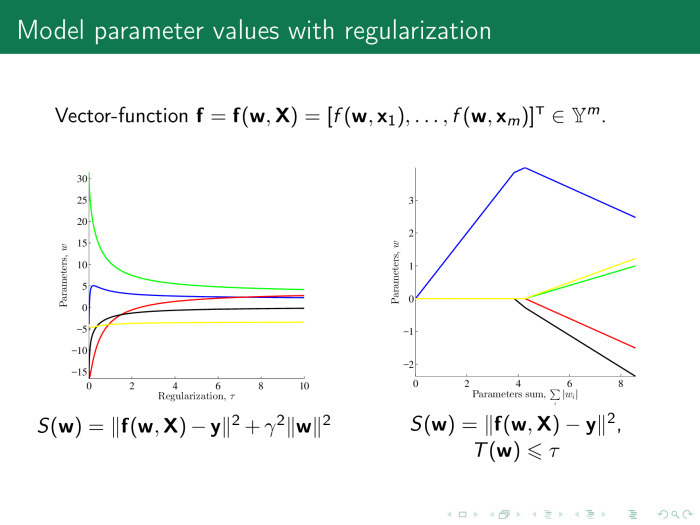
Как работают алгоритмы выбора признаков? Как правило, они используют функции ошибки. В линейной регрессии это суммы квадратов регрессионных остатков. И есть два типа алгоритмов выбора признаков. Первый тип — регуляризующие алгоритмы. Они кроме ошибки используют, как было сказано Константином Вячеславовичем в прошлой лекции, ещё и некоторый регуляризатор, штраф на значение параметров и какой-то коэффициент, который отвечает за важность штрафа.
Этот коэффициент может быть представлен в виде такого или такого штрафа. Веса должны быть не больше, чем некоторое значение ?.
В первом случае речь идет не о потере числа столбцов в матрице х, числа признаков, а только об увеличении устойчивости. Во втором случае мы как раз теряем значительное число столбцов.
При этом важно понимать, насколько столбцы коррелируют друг с другом. Как это выяснить?
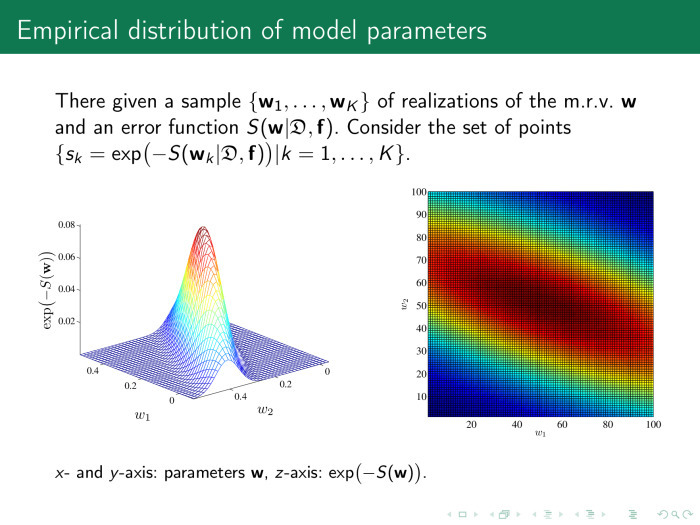
Рассмотрим пространство параметров нашей модели, вектор w, и вычислим значение ошибки в различных точках w. На рисунке справа показано само пространство, w1 или w2. Два веса отсемплированы, по 100 точек на каждый. Получается 100 пар весов. Каждая точка этого рисунка — значение функции ошибки. Слева, для удобства, то же самое —экспонента от минус значения функции ошибки.
Понятно, что оптимальные значения лежат где-то в точке 0,2–0,25 и это то, что мы ищем. А важность параметров определяется так: давайте из оптимального значения немножко качнем значений параметров. Если мы меняем w, функция ошибки практически не меняется. Зачем нам такой параметр нужен? Наверное, не нужен.
Здесь чуть качнули по оси w2 значение параметров, функция ошибки упала — прекрасно. Эта основа анализа пространства параметров — способ найти мультикоррелирующие признаки.
Откуда же берутся эти признаки? Давайте рассмотрим четыре основных способа порождения признаков. Первый — сами признаки. Откуда они? Мы берем временной ряд и рубим его на кусочки, например, кратные периоду. Или просто случайно, или с перехлестом. Эти порубленные сегменты мы складываем в матрицу Х, матрицу плана.
Второй способ. То же самое. Мы преобразуем временные ряды с помощью каких-то параметрических или непараметрических признаков.
Третий способ очень интересный и перспективный. Мы приближаем кусочки временного ряда какими-то моделями. Будем называть это локальным моделированием. И используем параметры этих моделей как признаки для прогноза.
Четвертое. Всё происходит в каком-то метрическом пространстве. Давайте найдем центроиды, сгущения кластеров в этом пространстве, и рассмотрим расстояния от каждого временного ряда до центроидов этих сгущений.

Плохая новость. Чтобы построить матрицу плана, отношения частот к семплированию временных рядов, если ряды разношкальные, должны быть краткими. При этом матрица плана разрастается. Правда, можно какие-то частички временных рядов выкинуть, как показано здесь. Весь временной ряд «длина светового дня» не нужен, нужна только одна точка в сутки, и матрица плана будет выглядеть так: 24 точки в строке — это потребление электроэнергии, а одна точка и ещё одна — длина светового дня.

Вот временной ряд. То, что мы уже рассмотрели. x ln x, по парам, — сумма, разница, произведение и разные другие комбинации.

Вот непараметрические трансформации. Просто усредненная сумма, стандартное отклонение. Гистограмма квантилей временного ряда.

Следующий вариант. Непараметрическое преобразование, преобразование Хаара. Мы берем среднее арифметическое и ставим его как одну точку вместо двух. Или берем разницу. Таким образом мы порождаем признак и снижаем число точек во временном ряде, соответственно снижаем размерность пространства.

Следующий набор порождающих функций — параметрические функции. С помощью них мы можем приближать временной ряд. Первое — этот приближенный ряд использовать вместо начального. Второе — использовать сами параметры, обозначенные как w.
Константа, парабола, гипербола, логарифмическая сигмоида, произведение, степенные функции, экспоненциальные функции.

Ещё один очень удобный класс — монотонные функции. Здесь знатоки нейронных сетей могут увидеть, например, функции активации, которые в сетях часто используются. Их можно использовать не только на выходе сетей, но и на входе. Это тоже сильно повышает качество прогноза.

Следующий класс порождающих функций — параметрические преобразования временных рядов. Здесь нам интересны сами параметры рядов. Мы берем вышеперечисленные функции и собираем их параметры в вектор b. У нас есть два типа параметров: первый — параметры самих аппроксимирующих функций, функции локальной аппроксимации, а второй вектор — параметры модели, те, которые были рассмотрены раньше, то есть параметры веса линейных комбинаций столбцов матрицы Х. Мы их можем настраивать одновременно, а можем настраивать итерационно и использовать их в том числе как столбцы матрицы плана. Другими словами, матрица плана, Х, итеративно меняется.
Откуда ещё мы можем получить параметры моделей? Буду рассматривать с конца. Сплайны при аппроксимации временного ряда имеют параметры, узлы сплайнов.
Быстрые преобразования Фурье. Мы можем использовать вместо временного ряда его спектр и тоже вставлять его в матрицу объект–признак.
Важный и хорошо работающий прием — использовать параметры метода «Singular structural analysis» или «Гусеница».

Этот метод работает следующим образом. Вначале мы строили матрицу Х — давайте построим новую матрицу по похожей схеме. Сейчас локальная матрица аппроксимации будет называться Н, и она будет построена так: сегмент временного ряда входит в строки матрицы не один за другим, а с перехлестом. Пусть здесь p = 1, а k = 3. Матрица по индексам будет выглядеть как 1,2,3; 2,3,4; 3,4,5 и так далее до конца.
Настраивать последний столбец по предыдущим мы будем тем же самым методом наименьших квадратов, а коэффициенты использовать в качестве наших признаков. В частности, этот прием хорошо работает при определении физической активности. Например, на руке у спортсмена есть часы и спортсмен хочет понять, насколько эффективно он двигается. У пловцов эта задача особенно популярна. Требуется определить не только тип заплыва, но ещё и мощность гребка.
Процессор там слабый, памяти никакой. И вместо того, чтобы решать большую задачу определения класса временного ряда или прогнозировать ряд, мы сразу же при поступлении данных его аппроксимируем похожим образом. Используем не аппроксимированный временной ряд, а параметры аппроксимации.
Работает это вот почему.
Здесь показан не сам временной ряд, а его логированные значения. Эта точка — значение ряда в данный момент времени и на один отсчет позднее. Понятно, что синус будет выглядеть как эллипс. Хорошая новость: размерность этого эллипса в пространстве логированных переменных всегда будет 2. Какой бы длины предысторию мы ни взяли в этом пространстве, размерность пространства всё равно останется фиксированной. А размерность пространства всегда можно определить с помощью сингулярного разложения.

Тогда каждый временной ряд мы можем представить в виде его главных компонент в сингулярном разложении. Соответственно, первой главной компонентой будет какой-то тренд, второй — главная гармоника и так далее по возрастанию гармоник. Веса этих компонент мы используем в качестве признаков в аппроксимирующих моделях.

Вот последний способ порождения признаков. Признаки метрические. Мы уже каким-то образом породили матрицу плана — давайте посмотрим, как её столбцы расположены в каком-то метрическом пространстве, например в евклидовом.
Мы назначаем метрику ? и выполняем кластеризацию строк матрицы объект–признак, Х.
Естественно, число расстояний от всех объектов выборки до всех объектов выборки — это мощность выборки в квадрате. Поэтому мы выбираем центры кластеров, измеряем расстояние от каждой строки до центра и используем полученные расстояния как признаки в матрице объект-признак.
На практике это выглядит следующим образом. Чтобы расстояние было вычислено корректно, мы сначала выравниваем временные ряды. Здесь показано шесть классов рядов для акселерометра: человек идет, идет вверх по ступеням, вниз по ступеням, стоит и лежит. Предлагается сначала выровнять ряды какой-то процедурой и получить, например, такие ряды. Дальше — вычислить средние значения или центроиды для каждого ряда.
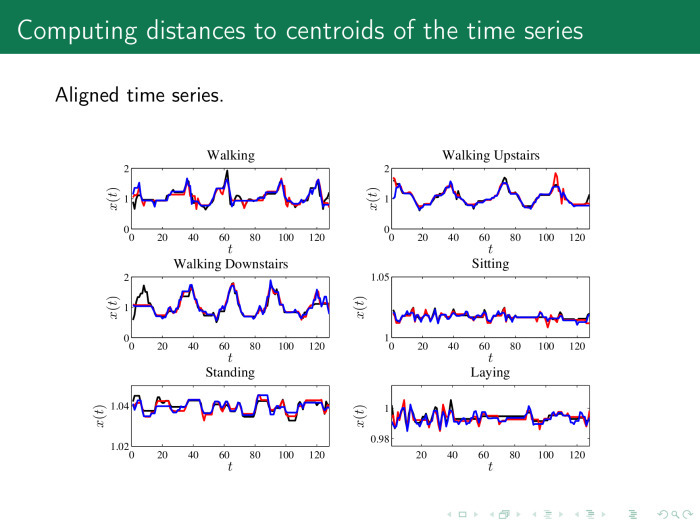
А потом вычислить расстояния от каждого временного ряда в матрице Х, объект–признак, до этих центроидов.
Что же получилось в результате порождения признаков разными способами? Давайте рассмотрим те же данные, что и вначале.
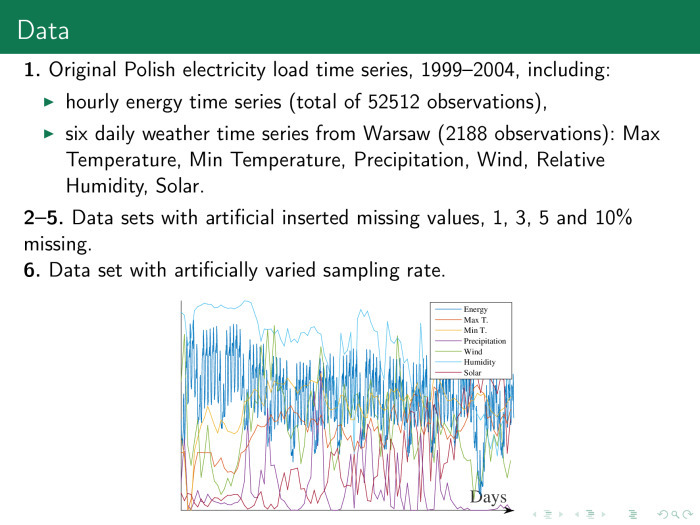
Это данные электропотребления в Польше, они почасовые. Кроме того, им сопутствуют разные временные ряды, которые их описывают. Вставим в эту выборку ещё и пропуски. Выбросим часть данных, например 3, 5, 10%. Заполним их, а потом попытаемся спрогнозировать значение всех рядов сразу.
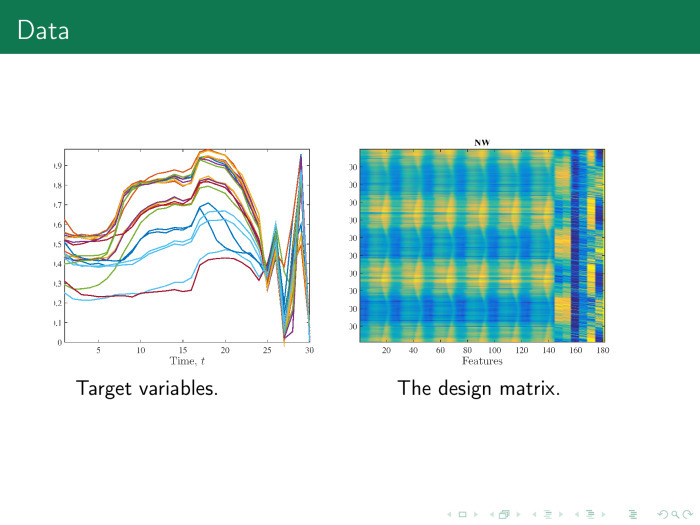
Справа мы получим вот такую матрицу объект–признак. Слева временные ряды, нарубленные на кусочки. Первые 24 временных ряда — сутки. Вместо зигзага следовало бы построить гистограмму.

Какие модели у нас есть? Самая хорошая модель — прогноз на завтра, то же самое, что и сегодня. Будем называть это базовым методом.
Линейная регрессия, которую мы рассмотрели вначале. Метод опорных векторов. Нейронная сеть random forest. Конечно, не хватило четвертого волшебного метода. Есть четыре метода, которые всегда работают хорошо, если задача вообще решается: нейронные сети, опорные вектора, random forest и градиентный бустинг.
Сравним, как работают четыре разных метода при различных способах порождения признаков. Вот опять эти четыре способа. Исторические временные ряды. Приближение временных рядов. И — расстояния от временных рядов до центроидов.
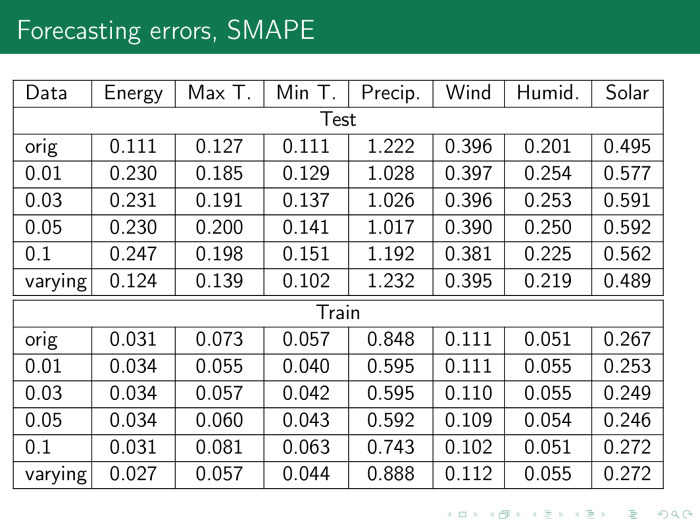
В результате строится такая табличка. Здесь значения — ошибка, фактически разность между фактом и прогнозом в процентах. Столбцы — это разное число пропусков.
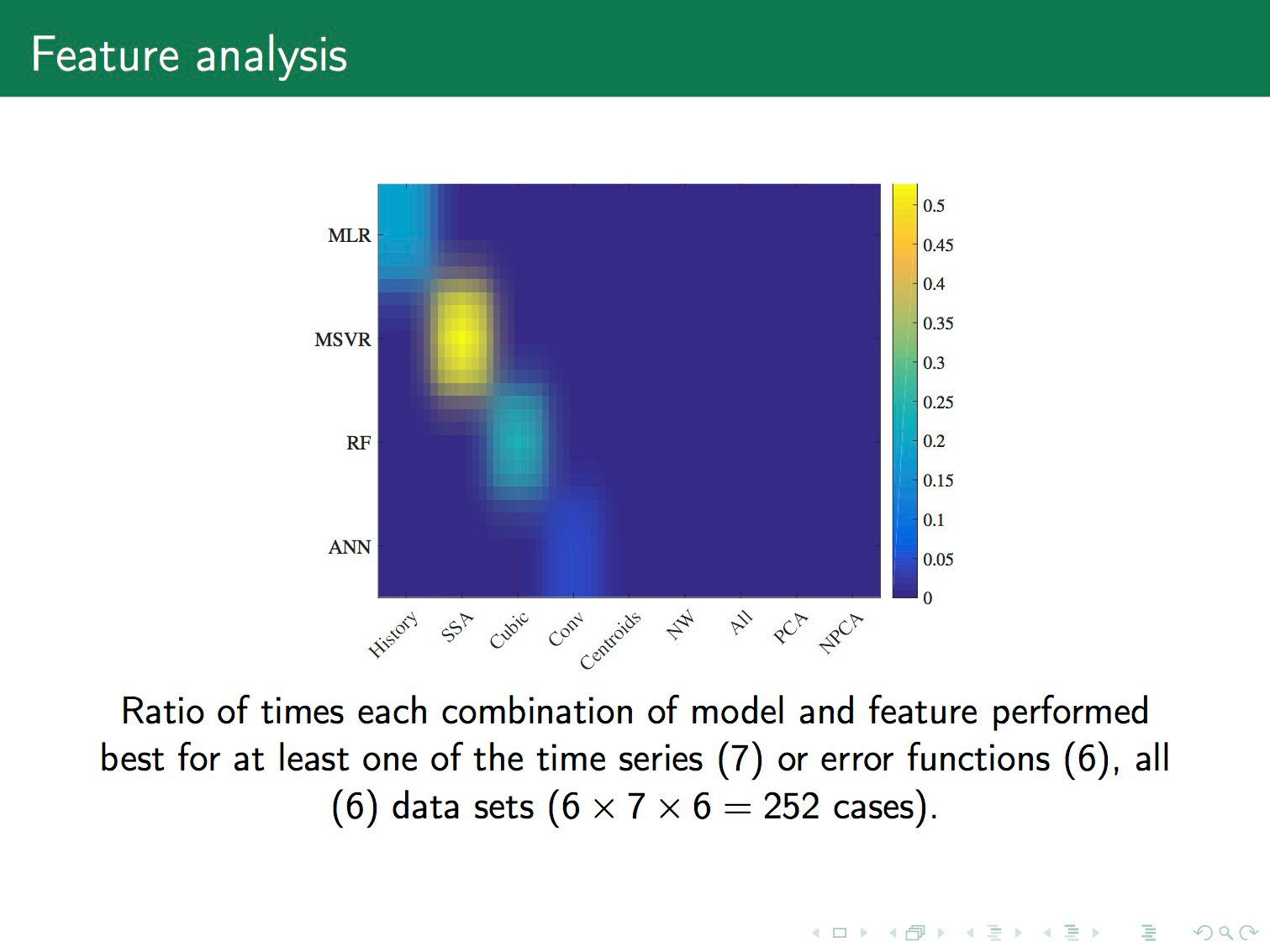
Лучше на неё смотреть следующим образом. Указанные пятна должны быть жесткими. Чем пятна больше, тем лучше. Это число вхождений пары модель–признак в хорошие комбинации, которые дают минимальную ошибку. Мы видим, что у нас хорошие пары — это линейная регрессия и неизмененный временной ряд. Support vector machine и значение ряда после преобразования гусеницы. Дальше random forest и кубическая аппроксимация. Нейронные сети и свёртки.

По временным рядам. Возьмем самые хорошие пары, в данном случае это support vector regression и гусеница. Посмотрим, насколько часто встречаются хорошие пары по разным временным рядам. Энергия, температура, влажность, ветер, солнце. При обучении хорошая пара оказалась только одна — support vector regression на исходных временных рядах. А на тесте у нас хорошие варианты, вы их видите на графике.
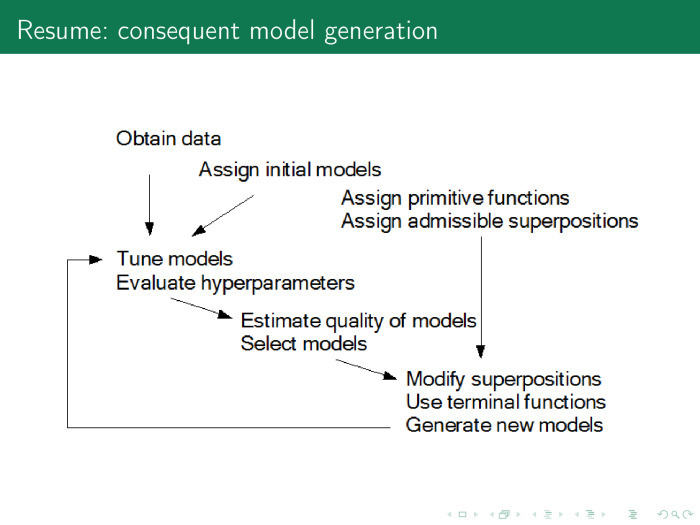
Как вообще устроена процедура порождения моделей? Есть данные, есть порождающие функции, есть какие-то хорошие модели, которые мы использовали раньше. Мы выполняем следующую цепочку: находим параметры модели и гиперпараметры, вычисляем качество модели, выбираем какие-то оптимальные модели, вовлекаем новые порождающие функции и их суперпозиции и продолжаем всё по кругу до тех пор, пока не получим хорошую модель. У меня всё, спасибо.
Под катом — лекция ведущего научного сотрудника РАН, доктора наук и главного редактора журнала «Машинное обучение и анализ данных» Вадима Стрижова, а также большинство слайдов.
Мы поговорим о способах порождения и выбора моделей на примере временных рядов интернета вещей.
Концепция интернета вещей появилась уже более десяти лет назад. От обычного интернета он отличается прежде всего тем, что запрос делает не человек, а устройство или сообщение в сети, которое взаимодействует с другими устройствами без человека.
Пример первый. Никому не хочется каждый месяц лезть в угол с фонариком, смотреть, сколько намотал счетчик электроэнергии, и потом идти ногами платить. Понятно, что современные счетчики мониторят не только почасовое потребление энергии в квартире, но даже знают, сколько из каждой розетки ушло энергии.
Второй вариант. Мониторинг здоровья человека. Примерном временных рядов, которые находятся в этой области, является следующее. Сейчас больным тетраплегией, у которых отказали конечности, ставят прямо на кортекс датчик размером с ладошку. Его не видно изнутри, он полностью закрыт. Он даёт 124 канала с поверхности кортекса с частотой 900 герц. По этим временным рядам мы можем прогнозировать движение конечностей, то, как он хочет двигаться.
Следующий пример — торговля. Сейчас кассиры на выходе из магазина стоят дорого, и очередь на выходе из магазина — это тоже не есть хорошо. Требуется создать такую систему и получить такие сигналы, когда человек с тележкой, проезжая мимо выхода, получает сразу все значения цен купленных им продуктов.
Последний довольно очевидный пример — автоматическое регулирование работы городских служб: светофоров, освещения, датчиков погоды, наводнений и т. д.

Вот первый пример временных рядов, с которыми мы будем работать. У нас есть почасовое потребление электроэнергии, максимальная и минимальная суточная температура, влажность, ветер, длина светового дня.

Второй пример временных рядов, который иерархически находятся над первым, — то же самое, только для каждой точки некоторого региона. В данном случае показан кусочек Европы, и вместе с этими временными рядами, в частности, в каждой точке снимается значение загрязнения воздуха.

Ещё более сложный пример — значения электрического поля. По оси ординат отложены частоты, по оси абсцисс — время. Это тоже временной ряд. Если прошлый временной ряд — декартово произведение времени на пространство на пространство, то здесь мы имемм декартово произведение времени на частоты.

Следующий временной ряд ещё более сложный. По оси абсцисс и ординат пространство, по оси аппликат — время. Таким образом, у нас есть много разных красивых временных рядов, и временной ряд необязательно содержит только время и значения. Он может содержать декартово произведение нескольких осей времен, частот, пространств и т. д.
Рассмотрим самый простой вариант. У нас есть временные ряды потребления электроэнергии небольшого города. Есть цена, объем потребления, длина светового дня, температура и т. д. Эти временные ряды периодичны. Потребление электроэнергии колеблется в течение года, в течение недели и в течение суток.

Возьмем произвольный день. Синий — временные ряды, красный — прогноз. 12 часов ночи, граждане засыпают, просыпается мафия. Временной ряд падает, потребление падает. Вся Москва ночью горит огнями, в общем-то, потому, что она окружена ТЭЦ, энергию девать некуда, и цена на электроэнергию может даже упасть ниже нуля, можно и доплачивать за электроэнергию — лишь бы потребляли.
6 часов, граждане просыпаются, едут на работу, пьют чай, потом работают, потом едут домой — этот цикл повторяется.
Задача — спрогнозировать по часам потребление электроэнергии на следующий день и закупить сразу всю электроэнергию на сутки. Иначе на следующий день придется доплачивать за разницу в потреблении, а это уже дороже.

Каким образом решается такая задача? Давайте на основе предыдущего временного ряда построим такую матрицу. Здесь по строкам расположены дни, примерно 40 дней по 24 часа. И мы легко можем увидеть здесь особые строчки — субботы и воскресенья. Видно, что в Анкаре — так же, как и в Москве, — в субботу люди ведут себя довольно активно, а в воскресенье отдыхают.
Каждый столбец — в данном случае 20 часов какого-то дня недели. Всего здесь пять недель.

Представим эту матрицу в формальном виде. Мы берем временной ряд за хвостик, по дням недели или по неделям сворачиваем, получаем матрицу объект–признак, где объект — день, а признак — час, и решаем стандартную задачу линейной регрессии.
С помощью этого значения мы ищем, например, 12 часов следующего дня. То, что мы прогнозируем, мы считаем y за всю нашу историю. Х — вся история, кроме этих 12 часов. Прогноз — скалярное произведение последней недели, векторы значений и наших весов, которые мы получаем, например, с помощью метода наименьших квадратов.
Что надо сделать, чтобы получить более точный прогноз? Давайте породим различные элементы модели. Мы их называем порождающими функциями или примитивами.

Можно с временным рядом сделать следующее: взять из него корень. Можно его оставить, можно взять временной ряд – корень из временного ряда, временной ряд – логарифм из временного ряда и т. п.
Таким образом, мы добавляем столбцы к матрице объект–признак, увеличиваем число столбцов, а число строк остается прежним.
Более того, для порождения признаков мы можем использовать полином Колмогорова-Габора. Первый член — сами временные ряды. Второй член — все произведения временных рядов. Третий — произведение троек временных рядов. И так далее, пока нам не надоест.
Коэффициент собираем со всего временного ряда — и опять получаем линейную модель. После этого получаем довольно приличный прогноз. И даже возникает подозрение, не переобучились ли мы, не слишком ли хорош прогноз?

Он астолько хорош, что параметры вообще потеряли свой смысл.
Предположим, строка матриц плана — это неделя, 7 дней, 168 часов. Есть данные, например, за три года. В году 52 недели. Тогда базовая матрица за три года — это 156 строк на 168 столбцов.

Если мы используем шесть временных рядов, которые я перечислю, — то есть вместе с потреблением ещё учтём цену, влажность, температуру и так далее, — то столбцов в матрице станет уже более 1000. А если будет ещё четыре порождающих функции, то это 4000 строк и 156 столбцов. То есть матрица сильно вырождена, и нормально решить линейное уравнение не представляется возможным. Что же делать?

Наверное, надо запустить процедуру выбора моделей. Для этого надо посмотреть, какие веса имеют смысл. На каждый час мы строим свою модель, и здесь по оси абсцисс показаны значения параметров модели по часам на следующие сутки. А по оси ординат стоят сами параметры. Мы видим желто-красную диагональ, значение весов побольше там, где есть свой час в модели за предыдущие дни.
Принцип простой. Прогноз на завтра на 12 часов зависит от значений за 12 часов предыдущего дня, позавчерашнего и т. п. Таким образом, мы можем оставить только эти значения, а всё остальное выбросить.

Что именно надо выбрасывать? Представим матрицу х как набор столбцов. Мы приближаем временной ряд y линейной — или необязательно линейной — комбинацией столбцов матрицы х. Нам хотелось бы найти такой столбец ?, который был бы поближе к y. Значительная часть алгоритмов выбора признаков выберет нам столбцы ?1 и ?2, если мы захотим оставить два столбца. Но среди тех, что мы породили, нам нужны ?3 и ?4. Они дают одновременно точную и устойчивую модель. Точную — потому что линейная комбинация?3 и ?4 в точности приближает y, а устойчивую — потому что они ортогональны.
Почему именно два столбца? Надо посмотреть, в каком пространстве мы работаем, сколько объектов в нарисованной выборке. Здесь три объекта. Матрица х содержит 3 строки и 6 столбцов.

Как работают алгоритмы выбора признаков? Как правило, они используют функции ошибки. В линейной регрессии это суммы квадратов регрессионных остатков. И есть два типа алгоритмов выбора признаков. Первый тип — регуляризующие алгоритмы. Они кроме ошибки используют, как было сказано Константином Вячеславовичем в прошлой лекции, ещё и некоторый регуляризатор, штраф на значение параметров и какой-то коэффициент, который отвечает за важность штрафа.
Этот коэффициент может быть представлен в виде такого или такого штрафа. Веса должны быть не больше, чем некоторое значение ?.
В первом случае речь идет не о потере числа столбцов в матрице х, числа признаков, а только об увеличении устойчивости. Во втором случае мы как раз теряем значительное число столбцов.
При этом важно понимать, насколько столбцы коррелируют друг с другом. Как это выяснить?

Рассмотрим пространство параметров нашей модели, вектор w, и вычислим значение ошибки в различных точках w. На рисунке справа показано само пространство, w1 или w2. Два веса отсемплированы, по 100 точек на каждый. Получается 100 пар весов. Каждая точка этого рисунка — значение функции ошибки. Слева, для удобства, то же самое —экспонента от минус значения функции ошибки.
Понятно, что оптимальные значения лежат где-то в точке 0,2–0,25 и это то, что мы ищем. А важность параметров определяется так: давайте из оптимального значения немножко качнем значений параметров. Если мы меняем w, функция ошибки практически не меняется. Зачем нам такой параметр нужен? Наверное, не нужен.
Здесь чуть качнули по оси w2 значение параметров, функция ошибки упала — прекрасно. Эта основа анализа пространства параметров — способ найти мультикоррелирующие признаки.
Откуда же берутся эти признаки? Давайте рассмотрим четыре основных способа порождения признаков. Первый — сами признаки. Откуда они? Мы берем временной ряд и рубим его на кусочки, например, кратные периоду. Или просто случайно, или с перехлестом. Эти порубленные сегменты мы складываем в матрицу Х, матрицу плана.
Второй способ. То же самое. Мы преобразуем временные ряды с помощью каких-то параметрических или непараметрических признаков.
Третий способ очень интересный и перспективный. Мы приближаем кусочки временного ряда какими-то моделями. Будем называть это локальным моделированием. И используем параметры этих моделей как признаки для прогноза.
Четвертое. Всё происходит в каком-то метрическом пространстве. Давайте найдем центроиды, сгущения кластеров в этом пространстве, и рассмотрим расстояния от каждого временного ряда до центроидов этих сгущений.

Плохая новость. Чтобы построить матрицу плана, отношения частот к семплированию временных рядов, если ряды разношкальные, должны быть краткими. При этом матрица плана разрастается. Правда, можно какие-то частички временных рядов выкинуть, как показано здесь. Весь временной ряд «длина светового дня» не нужен, нужна только одна точка в сутки, и матрица плана будет выглядеть так: 24 точки в строке — это потребление электроэнергии, а одна точка и ещё одна — длина светового дня.

Вот временной ряд. То, что мы уже рассмотрели. x ln x, по парам, — сумма, разница, произведение и разные другие комбинации.

Вот непараметрические трансформации. Просто усредненная сумма, стандартное отклонение. Гистограмма квантилей временного ряда.

Следующий вариант. Непараметрическое преобразование, преобразование Хаара. Мы берем среднее арифметическое и ставим его как одну точку вместо двух. Или берем разницу. Таким образом мы порождаем признак и снижаем число точек во временном ряде, соответственно снижаем размерность пространства.

Следующий набор порождающих функций — параметрические функции. С помощью них мы можем приближать временной ряд. Первое — этот приближенный ряд использовать вместо начального. Второе — использовать сами параметры, обозначенные как w.
Константа, парабола, гипербола, логарифмическая сигмоида, произведение, степенные функции, экспоненциальные функции.

Ещё один очень удобный класс — монотонные функции. Здесь знатоки нейронных сетей могут увидеть, например, функции активации, которые в сетях часто используются. Их можно использовать не только на выходе сетей, но и на входе. Это тоже сильно повышает качество прогноза.

Следующий класс порождающих функций — параметрические преобразования временных рядов. Здесь нам интересны сами параметры рядов. Мы берем вышеперечисленные функции и собираем их параметры в вектор b. У нас есть два типа параметров: первый — параметры самих аппроксимирующих функций, функции локальной аппроксимации, а второй вектор — параметры модели, те, которые были рассмотрены раньше, то есть параметры веса линейных комбинаций столбцов матрицы Х. Мы их можем настраивать одновременно, а можем настраивать итерационно и использовать их в том числе как столбцы матрицы плана. Другими словами, матрица плана, Х, итеративно меняется.
Откуда ещё мы можем получить параметры моделей? Буду рассматривать с конца. Сплайны при аппроксимации временного ряда имеют параметры, узлы сплайнов.
Быстрые преобразования Фурье. Мы можем использовать вместо временного ряда его спектр и тоже вставлять его в матрицу объект–признак.
Важный и хорошо работающий прием — использовать параметры метода «Singular structural analysis» или «Гусеница».

Этот метод работает следующим образом. Вначале мы строили матрицу Х — давайте построим новую матрицу по похожей схеме. Сейчас локальная матрица аппроксимации будет называться Н, и она будет построена так: сегмент временного ряда входит в строки матрицы не один за другим, а с перехлестом. Пусть здесь p = 1, а k = 3. Матрица по индексам будет выглядеть как 1,2,3; 2,3,4; 3,4,5 и так далее до конца.
Настраивать последний столбец по предыдущим мы будем тем же самым методом наименьших квадратов, а коэффициенты использовать в качестве наших признаков. В частности, этот прием хорошо работает при определении физической активности. Например, на руке у спортсмена есть часы и спортсмен хочет понять, насколько эффективно он двигается. У пловцов эта задача особенно популярна. Требуется определить не только тип заплыва, но ещё и мощность гребка.
Процессор там слабый, памяти никакой. И вместо того, чтобы решать большую задачу определения класса временного ряда или прогнозировать ряд, мы сразу же при поступлении данных его аппроксимируем похожим образом. Используем не аппроксимированный временной ряд, а параметры аппроксимации.
Работает это вот почему.
Здесь показан не сам временной ряд, а его логированные значения. Эта точка — значение ряда в данный момент времени и на один отсчет позднее. Понятно, что синус будет выглядеть как эллипс. Хорошая новость: размерность этого эллипса в пространстве логированных переменных всегда будет 2. Какой бы длины предысторию мы ни взяли в этом пространстве, размерность пространства всё равно останется фиксированной. А размерность пространства всегда можно определить с помощью сингулярного разложения.

Тогда каждый временной ряд мы можем представить в виде его главных компонент в сингулярном разложении. Соответственно, первой главной компонентой будет какой-то тренд, второй — главная гармоника и так далее по возрастанию гармоник. Веса этих компонент мы используем в качестве признаков в аппроксимирующих моделях.

Вот последний способ порождения признаков. Признаки метрические. Мы уже каким-то образом породили матрицу плана — давайте посмотрим, как её столбцы расположены в каком-то метрическом пространстве, например в евклидовом.
Мы назначаем метрику ? и выполняем кластеризацию строк матрицы объект–признак, Х.
Естественно, число расстояний от всех объектов выборки до всех объектов выборки — это мощность выборки в квадрате. Поэтому мы выбираем центры кластеров, измеряем расстояние от каждой строки до центра и используем полученные расстояния как признаки в матрице объект-признак.
На практике это выглядит следующим образом. Чтобы расстояние было вычислено корректно, мы сначала выравниваем временные ряды. Здесь показано шесть классов рядов для акселерометра: человек идет, идет вверх по ступеням, вниз по ступеням, стоит и лежит. Предлагается сначала выровнять ряды какой-то процедурой и получить, например, такие ряды. Дальше — вычислить средние значения или центроиды для каждого ряда.

А потом вычислить расстояния от каждого временного ряда в матрице Х, объект–признак, до этих центроидов.
Что же получилось в результате порождения признаков разными способами? Давайте рассмотрим те же данные, что и вначале.

Это данные электропотребления в Польше, они почасовые. Кроме того, им сопутствуют разные временные ряды, которые их описывают. Вставим в эту выборку ещё и пропуски. Выбросим часть данных, например 3, 5, 10%. Заполним их, а потом попытаемся спрогнозировать значение всех рядов сразу.

Справа мы получим вот такую матрицу объект–признак. Слева временные ряды, нарубленные на кусочки. Первые 24 временных ряда — сутки. Вместо зигзага следовало бы построить гистограмму.

Какие модели у нас есть? Самая хорошая модель — прогноз на завтра, то же самое, что и сегодня. Будем называть это базовым методом.
Линейная регрессия, которую мы рассмотрели вначале. Метод опорных векторов. Нейронная сеть random forest. Конечно, не хватило четвертого волшебного метода. Есть четыре метода, которые всегда работают хорошо, если задача вообще решается: нейронные сети, опорные вектора, random forest и градиентный бустинг.
Сравним, как работают четыре разных метода при различных способах порождения признаков. Вот опять эти четыре способа. Исторические временные ряды. Приближение временных рядов. И — расстояния от временных рядов до центроидов.

В результате строится такая табличка. Здесь значения — ошибка, фактически разность между фактом и прогнозом в процентах. Столбцы — это разное число пропусков.

Лучше на неё смотреть следующим образом. Указанные пятна должны быть жесткими. Чем пятна больше, тем лучше. Это число вхождений пары модель–признак в хорошие комбинации, которые дают минимальную ошибку. Мы видим, что у нас хорошие пары — это линейная регрессия и неизмененный временной ряд. Support vector machine и значение ряда после преобразования гусеницы. Дальше random forest и кубическая аппроксимация. Нейронные сети и свёртки.

По временным рядам. Возьмем самые хорошие пары, в данном случае это support vector regression и гусеница. Посмотрим, насколько часто встречаются хорошие пары по разным временным рядам. Энергия, температура, влажность, ветер, солнце. При обучении хорошая пара оказалась только одна — support vector regression на исходных временных рядах. А на тесте у нас хорошие варианты, вы их видите на графике.

Как вообще устроена процедура порождения моделей? Есть данные, есть порождающие функции, есть какие-то хорошие модели, которые мы использовали раньше. Мы выполняем следующую цепочку: находим параметры модели и гиперпараметры, вычисляем качество модели, выбираем какие-то оптимальные модели, вовлекаем новые порождающие функции и их суперпозиции и продолжаем всё по кругу до тех пор, пока не получим хорошую модель. У меня всё, спасибо.
Поделиться с друзьями


sh_vit
спасибо!