Я много писал об алгоритме коллапса волновой функции (Wave Function Collapse). Этот алгоритм, разработанный Максимом Гуминым в 2016 году, генерирует тайловые карты и пиксельные текстуры на основании удовлетворения ограничениям с дополнительной рандомизацией [перевод на Хабре]. Но знали ли вы, что большинство основных идей для него взято из статьи, написанной больше десятка лет назад? Сегодня мы рассмотрим диссертацию 2007 года на степень PhD Пола Меррела Model Synthesis и некоторые из разработанных им расширений алгоритма, в частности, Modifying in Blocks.

Model Synthesis

Идея Model Synthesis очень похожа на WFC, по которому я написал целый туториал. Но в этой статье мы опишем идею с нуля.

Model Synthesis начинает с передачи примера тайловой карты, которая используется алгоритмом для того, чтобы учиться, какие тайлы могут располагаться друг рядом с другом при построении модели. Затем для выходного результата инициализируется пустая сетка ячеек. Каждая ячейка имеет список «потенциальных» тайлов, которые могут её заполнить.

Изначально допустим любой тайл. Основной цикл выбирает ячейку и выбирает для неё заданный тайл, помечая все остальные как недопустимые. Затем он распространяет последствия этого выбора при помощи алгоритма AC4, то есть помечает тайл как недопустимый для текущей ячейки, если все его валидные смежные ячейки уже недопустимы. После распространения цикл сбрасывается и мы выбираем другую ячейку, для которой нужно выбрать тайл.

Рано или поздно у каждой ячейки останется только один возможный тайл, после чего генерируется карта. В случае сложных наборов тайлов могут возникать противоречия (ячейки, в которых невозможен ни один из тайлов), и для их решения требуется более сложный подход под названием Modifying in Blocks, описанный ниже.

Эта процедура очень похожа на простой солвер ограничений, за исключением способа выбора ячеек и тайлов. Model Synthesis описывает то, что, по моему мнению, является фундаментальной особенностью подобной генерации: любой солвер на основании ограничений может быть при помощи случайного выбора преобразован в генератор на основе ограничений. Похоже, такой подход впервые был использован именно в этой статье — предыдущие решениях задачи синтеза текстур были по своей природе более статистическими.


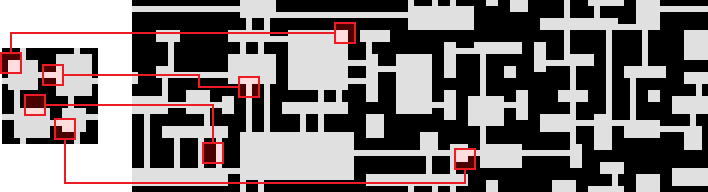
Иллюстрация из статьи, при помощи добавления внешних ограничений демонстрирующая, что Model Synthesis по своей природе является солвером ограничений

Разница между Model Synthesis и Wave Function Collapse

• MS выбирает ячейки на основании линейного сканирования. WFC добавляет эвристику «минимальной энтропии» для выбора сложных в установке тайлов.

• MS в основном делает упор на объёмные тайлы и 3D-сцены, а WFC больше занимается попиксельной генерацией и синтезом текстур (хотя оба алгоритма одинаково способны решать и те, и другие задачи)

Типичный пример MS


Типичный пример WFC

• В WFC добавлена модель Overlapped Model, которая обучается локальному соседству, а не только непосредственным соседям.

Созданная Максимом иллюстрация Overlapped Model

Пол Меррелл написал статью о конкретных различиях между ModelSynthesis и WFC. Также мне нравится заметка @expad.

Почему про Model Synthesis забыли?

По моему опыту, добавленные в WFC особенности приятны, но не уникальны. Мы по-прежнем можем получать очень хорошие результаты при помощи Model Synthesis, а их базовые концепции одинаковы. Так почему же эта идея прозябала десять лет, прежде чем Максим не увидел её потенциал и не создал репозиторий?

В Model Synthesis используются 3D-тайлы, которые довольно сложно проектировать, и код на C++, который сложно заставить работать. В WFC появился большой набор примеров, и все они были простыми изображениями. Благодаря переходу на 2D-изображения использование и поведение проекта мгновенно становится намного понятнее, и этому он обязан анимациям, демонстрирующим множество возможных тайлов, обновляемое в процессе анимации. Когда я пишу туториалы, именно по этой причине я сначала знакомлю с идеями в 2D и добавляю анимации.

Или же причина может быть более скучной. Веб-сайт Model Synthesis был недоступен в течение нескольких лет, а Wave Function Collapse — гораздо более интересное название, напоминающее о квантовой физике.

Modifying in Blocks

Синтез на основе ограничений, будь то Model Synthesis или Wave Function Collapse, страдает от одного сложного аспекта: мы можем прийти к противоречиям — ситуациям, когда решение невозможно и никак нельзя продвинуться дальше. Подобные трудности являются неотъемлемой частью солверов ограничений, так как пространство задачи в целом является NP-полным.

Чтобы проиллюстрировать эту проблему, я воспользовался одним из примеров Пола Меррелла — Escheresque (с его разрешения). Escheresque — это 3D-набор тайлов, намеренно сделанный сложным; многие тайлы имеют довольно далеко распространяющиеся связи друг с другом, а пустое пространство имеет низкий вес, что вынуждает к максимальной заполненности сцены. Поэтому противоречия возникают достаточно часто.


Типичная сцена, сгенерированная на основе сэмпла Escheresque

Для устранения противоречий WFC использует чрезвычайно простой подход. Если противоречие возникает, он просто перезапускает процесс сначала. Если противоречия редки, решение будет найдено после нескольких перезапусков. К сожалению, такой подход не масштабируется — если нужно генерировать результаты всё большего размера, вероятности противоречий растут, пока не станет совершенно невозможно получить успешный результат, сколько бы раз вы ни перезапускали алгоритм.

Вот стандартный WFC с сэмплом Escheresque. Как видите, противоречия достаточно часты и WFC постоянно выполняет перезапуск. Шансы заполнения всего объёма 30x30x10 крайне малы.


Альтернативный подход, который я использую в Tessera, стандартный для многих солверов ограничений — это поиск с возвратом. Вместо того, чтобы при возникновении противоречия начинать с нуля, поиск с возвратом откатывается к последнему хорошему состоянию и записывает дополнительную информацию, чтобы мы не пробовали одно действие дважды. Поиск с возвратом решает проблему противоречий, но заменяет её возможностью захождения алгоритма в тупик.

Захождение в тупик происходит, когда частичное решение неразрешимо, но алгоритм не знает, как вернуться из него и вместо этого многократно исследует вариации этого частичного решения. Для большинства наборов тайлов такие кроличьи норы встречаются реже, чем явные противоречия, поэтому можно получить более впечатляющие результаты, но в конечном итоге такой подход всё равно не масштабируется: при необходимости достаточно объёмного результата он зайдёт в тупик и застрянет.

После включения поиска с возвратом для сэмпла Escheresque результаты становятся лучше, но рано или поздно он находит какую-нибудь слишком сложную область и застревает, пытаясь её исправить.


Поэтому вместо этого Меррелл использовал другой подход под названием Modifying In Blocks (также называемый «модификацией по частям»). Когда алгоритму нужно сгенерировать большую площадь, он решает её не как одну большую задачу, а разбивает её на несколько задач поменьше. Область результата разбивается на несколько пересекающихся блоков. После чего происходит солвинг отдельных блоков. Если достигнуто противоречие, перезапуск требуется только для одного блока, а не всего решения. Таким образом, это компромисс между полными перезапусками и поиском с возвратом. Мы надеемся, что перезапуски устранят противоречия, а блоки достаточно велики, чтобы избежать кроличьих нор, поэтому мы можем генерировать чрезвычайно большие результаты без увеличения общего количества неудач.

Запустив этот алгоритм с сэмплом Escheresque, мы увидим, что он успешно генерирует всю область, однако он потребовал тщательной настройки и обработки ошибок, которая не видна в анимации.

Подробности

Очевидно, что если мы просто будем оценивать каждый блок по отдельности, то результат не будет целостным. Весь смысл ограничений соседних ячеек в том, чтобы тайлы соединялись друг с другом. Но как оказывается, выбор способа оценки блоков очень широк.

Очевидным решением было бы разбиение всего пространства на граничащие друг с другом блоки, чтобы каждая ячейка принадлежала только одному блоку. Затем мы генерируем по одному блоку за раз, начав с одного угла и используя уже сгенерированные соседние блоки в качестве входных ограничений для общих границ текущего блока. Во многих случаях такой подход сработает.


Блоки без пересечений с простым набором тайлов из травы и дорожек

Однако в генерировании WFC мешает то, что солвер ограничений рассматривает в качестве релевантных только тайлы внутри области генерации. Это значит, что для некоторых наборов тайлов он может генерировать результаты, которые невозможно расширить без создания противоречия. Чтобы избежать этого, Пол Меррелл использует немного иную схему.

При генерации каждого блока он ограничивает все границы блока. Некоторые из этих ограничений берутся из ранее сгенерированных блоков, но для других сторон блока, которые пока открыты, он фиксирует границу на гарантированно хорошем наборе тайлов. В сэмпле Escheresque (см. видео выше) используется поверхность из плоского основания, над которым нет ничего, кроме воздуха, а в наборе тайлов с травой и дорожками используется сплошной зелёный фон (см. анимацию ниже).

Зафиксировав все границы, мы гарантируем, что каждый блок более автономен и его проще расширять. Блоки выстроены так, что накладываются друг на друга, поэтому все эти фиксированные границы постепенно перезаписываются, но они сильно повышают вероятность успеха, поскольку мы уже знаем хотя бы одну структуру тайлов, которая подходит. Если возникнет слишком много противоречий/перезапусков, всегда можно просто сдаться и откатиться к гарантированно хорошим тайлам.


Блоки намеренно наложены друг на друга и мы начинаем с «гарантированно хорошего» сплошного зелёного фона. После оценки каждого блока у нас получается полностью непротиворечивый набор тайлов.

Оценка

Я поэкспериментировал с сэмплом Escheresque. Как уже говорилось, это очень сложный для правильной генерации набор тайлов. Я выяснил, что он очень чувствителен к порядку генерации и предпочитает определённые линейные сканы для min-энтропии. Ни WFC с перезапусками, ни мой собственный код поиска с возвратом не имел бы ни малейшего шанса масштабирования до результата объёмом 30x30x10. Алгоритм Modifying by Blocks смог добиться гораздо больших объёмов, однако ему всё равно требуются достаточно щедные настройки перезапуска блоков и обработка ошибок.

Производительность тоже не особо велика, так как из-за наложения блоков приходится делать много избыточной работы. Но алгоритм масштабируется немного лучше — наивный WFC может столкнуться с проблемами больших результатов, поскольку для генерации следующей ячейки ему нужно многократно сканировать для минимальной энтропии, а эту проблему мы избегаем благодаря линейному сканированию.

В целом, этот инструмент показался мне интересным. Большое количество параметров настройи и необходимость предварительного указания гарантированно хорошей схемы тайлов ограничивает обобщённость методики. Тем не менее, я нашёл интересные способы применения Modifying in Blocks, о которых я подробно расскажу в следующей статье.