Привет, Хабр!
Dropout и Batch Normalization очень хороши в оптимизации процесса обучения и борьбе с одной из основных проблем ml — переобучением.
Dropout предполагает случайный кик нейронов из процесса обучения, обеспечивает, чтобы нейронная сеть не стала слишком зависимой от любого одного узла. Сравнить это можно с dropout в спортивных играх. Там это стратегия, которая заставляет каждого игрока команды играть лучше, а не полагаться только на одного звездного товарища.
Batch Normalization в свою очередь улучшает производительность и стабильность нейронных сетей путем нормализации входных данных каждого слоя.
Dropout
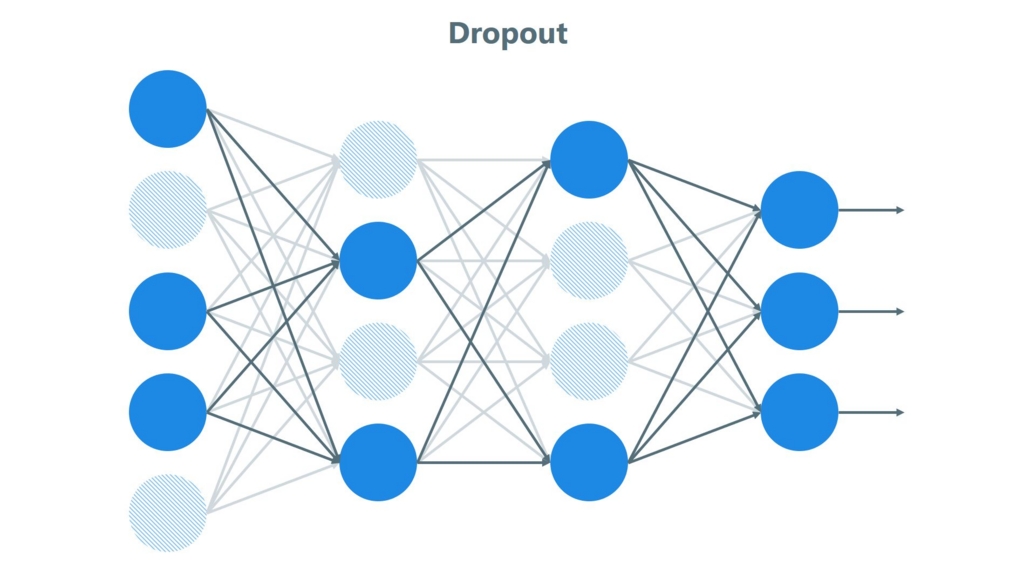
Основная идея Dropout заключается в случайном «выключении» (то есть временном исключении из обучения) определенного процента нейронов в сети на каждом шаге обучения. Это означает, что во время каждого прохода обучения (или каждой эпохи) случайно выбранный набор нейронов игнорируется. Это помогает предотвратить чрезмерную зависимость модели от конкретных путей и узлов в сети, что может привести к переобучению.
Сначала выбирается вероятность p, с которой каждый нейрон будет исключаться. Обычно pнаходится в диапазоне от 0.2 до 0.5.
Для каждого слоя, где применяется Dropout, генерируется случайная маска. Эта маска имеет ту же размерность, что и слой, и каждый её элемент является бинарным (0 или 1), где 1 соответствует активации нейрона, а 0 — его отключению. Эта маска генерируется заново для каждого прохода обучения и для каждого обучающего примера. Активации нейронов умножаются на эту маску, эффективно «выключая» некоторые нейроны.
В процессе обратного распространения ошибки, градиенты рассчитываются только для активных нейронов. Нейроны, которые были временно «выключены», не получают обновлений весов.
Во время тестирования или инференции Dropout отключается. Однако, активации нейронов масштабируются на коэффициент, равный вероятности p, чтобы компенсировать большее количество активных нейронов по сравнению с обучением. Это масштабирование помогает сохранить общую сумму активаций на похожем уровне между обучением и тестированием.
Математически, Dropout можно интерпретировать как ансамблевый метод. Каждый проход обучения использует случайно отобранную «тонкую» сеть, что похоже на обучение множества разных моделей и усреднение их прогнозов.
Подходы к определению оптимальной степени Dropout
1. Выбор степени Dropout в зависимости от типа сети: В разных типах сетей, таких как многослойные перцептроны (MLP), сверточные нейронные сети (CNN) и рекуррентные нейронные сети (RNN), может потребоваться различная степень Dropout.
Многослойные перцептроны (MLP)
Сети с плотными слоями (Dense layers): В таких сетях обычно используются значения Dropout от 0.2 до 0.5. Это помогает предотвратить переобучение, поскольку плотные слои склонны к запоминанию шума в данных. Необходимо провести серию экспериментов для определения оптимальной степени Dropout, учитывая конкретную задачу и сложность данных.
Сверточные нейронные сети (CNN)
— Положение слоев DropВ CNN Dropout часто помещают после сверточных и пулинговых слоев. Это помогает снизить переадаптацию к тренировочным данным, сохраняя при этом пространственные особенности изображений.
— Меньшие значения: Для CNN значения Dropout обычно ниже, чем для MLP, так как сверточные слои менее склонны к переобучению. Общие значения находятся в диапазоне от 0.1 до 0.3.
Рекуррентные нейронные сети (RNN), включая LSTM
— Dropout для входных и рекуррентных соединений: В RNN, включая LSTM, важно различать Dropout для входных данных и рекуррентных соединений.
— Для входных данных Dropout может быть более высоким (до 0.5), чтобы уменьшить зависимость от конкретных входных характеристик.
— Для рекуррентных соединений, рекомендуется более низкий уровень Dropout (например, от 0.1 до 0.2), поскольку слишком высокий уровень Dropout может нарушить передачу информации во времени и сделать обучение нестабильным.
2. Определение подходящей степени Dropout: Общепринятое значение для Dropout в скрытых слоях колеблется между 0.5 и 0.8, при этом более высокие значения чаще используются для входных слоев.
Для входных слоев часто используются более высокие значения Dropout, так как они имеют более прямое воздействие на входные данные. Значения в диапазоне от 0.5 до 0.8 помогают снизить риск переобучения на специфические особенности входных данных, особенно в задачах, связанных с большим количеством признаков или высокой размерностью.
В скрытых слоях обычно рекомендуются значения от 0.5 до 0.7. Это помогает предотвратить чрезмерную адаптацию модели к тренировочным данным, сохраняя при этом достаточное количество активных нейронов для эффективного обучения.
3. Grid Search для оптимизации параметров: Вместо того чтобы угадывать подходящую степень Dropout, можно протестировать различные значения систематически.
4. Использование ограничения веса: Веса сети могут увеличиваться в размерах в ответ на вероятностное удаление активаций слоя. Чтобы противодействовать этому, можно наложить ограничение на веса, чтобы норма всех весов в слое была ниже определенного значения.
5. Использование наименьших наборах данных: Dropout более хорош на задачах, где количество обучающих данных ограничено, и модель склонна к переобучению. На задачах с большим объемом обучающих данных преимущества от использования Dropout могут быть менее заметны.
Пару пример дропаута
В Keras мы можем всего за десять строчек создать простую нейронную сеть с одним скрытым слоем и дропаутом:
from keras.models import Sequential
from keras.layers import Dense, Dropout
model = Sequential([
Dense(64, activation='relu', input_shape=(20,)),
Dropout(0.5), # Применение 50% Dropout
Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])В Pytorch может выглядеть так:
import torch
import torch.nn as nn
import torch.nn.functional as F
class SimpleNN(nn.Module):
def __init__(self):
super(SimpleNN, self).__init__()
self.fc1 = nn.Linear(20, 64)
self.dropout = nn.Dropout(0.5) # 50% Dropout
self.fc2 = nn.Linear(64, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = torch.sigmoid(self.fc2(x))
return x
model = SimpleNN()Создадим модель для классификации изображений, например, используя набор данных MNIST. Модель будет содержать несколько сверточных слоев, слои пулинга и полносвязные слои, между которыми будут располагаться слои Dropout:
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
from tensorflow.keras.models import Sequential
model = Sequential([
# Сверточные и пулинговые слои
Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
MaxPooling2D((2, 2)),
Conv2D(64, (3, 3), activation='relu'),
MaxPooling2D((2, 2)),
Conv2D(64, (3, 3), activation='relu'),
# Плоский слой для преобразования данных из 2D в 1D
Flatten(),
# Полносвязные слои с Dropout
Dense(64, activation='relu'),
Dropout(0.5),
Dense(32, activation='relu'),
Dropout(0.5),
# Выходной слой
Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
Inverted Dropout
Inverted Dropout — это популярная вариация стандартного Dropout. Как и в стандартном Dropout, нейроны в слое сети отключаются случайным образом с вероятностью p (например, 50% нейронов могут быть отключены). Однако, в отличие от стандартного Dropout, не просто устанавливается 0 в выключенных нейронах.
Во время каждой итерации обучения для каждого слоя, где применяется Dropout, генерируется маска Dropout. Маска — это массив, содержащий 0 и 1, размер которого соответствует количеству нейронов в слое. Каждый элемент маски генерируется независимо и имеет вероятность p (гиперпараметр) быть равным 1 и вероятность1-p быть равным 0.
Маска применяется к активациям (выходам нейронов) данного слоя. Это означает, что активации нейронов, соответствующие 0 в маске, устанавливаются в 0, эффективно «выключая» эти нейроны во время текущей итерации обучения.
В отличие от традиционного Dropout, Inverted Dropout масштабирует активные нейроны так, чтобы суммарная активность слоя оставалась постоянной. Это делается путем деления активаций на вероятность сохранения 1-p. Таким образом, средний вклад каждого активного нейрона увеличивается, компенсируя отсутствие выключенных нейронов.
Batch Normalization
Batch Normalization (BN) предназначен для улучшения скорости, производительности и стабильности обучения нейронных сетей.
В основе Batch Normalization лежит решение проблемы «внутреннего ковариационного сдвига» (Internal Covariate Shift). Этот термин описывает явление, при котором распределение входных данных каждого слоя нейронной сети меняется в процессе обучения, из-за чего сети становится сложнее обучать. Это происходит из-за того, что параметры предыдущих слоев изменяются во время обучения, влияя на данные текущего слоя.
Batch Normalization решает эту проблему, нормализуя выход каждого слоя. Нормализация заключается в преобразовании входных данных каждого слоя таким образом, чтобы среднее значение было приближено к нулю, а стандартное отклонение — к единице. Это делает сеть менее чувствительной к масштабу входных данных и улучшает общую стабильность процесса обучения.
К примеру для мини-пакета
 алгоритм будет следующим:
алгоритм будет следующим:где m — размер мини-пакета, BN трансформирует каждый вход xi следующим образом:
1. Вычисление среднего:

2. Вычисление дисперсии:

3. Нормализация:
 , где ϵ — маленькое число для избежания деления на ноль.
, где ϵ — маленькое число для избежания деления на ноль.4. Масштабирование и сдвиг:
 , где γ и β — параметры, которые сеть обучается настраивать.
, где γ и β — параметры, которые сеть обучается настраивать.Интеграция в различные типы нейронных сетей
Интеграция в сверточные нейронные сети (CNN)
В CNN, BN обычно размещается сразу после сверточных слоев (Convolutional Layers) и перед активационной функцией, такой как ReLU. Порядок обычно следующий: Свертка → Batch Normalization → Активация.
В сверточных слоях BN применяется отдельно к каждому каналу выходных данных свертки. Это означает, что для каждого фильтра сверточного слоя вычисляется собственное среднее и дисперсия.
При этом сохраняется пространственная структура выходных данных, т.е. нормализация не влияет на пространственное расположение признаков.
В некоторых случаях BN может служить регуляризатором, уменьшая необходимость в Dropout.
Интеграция в рекуррентные нейронные сети (RNN)
Применение BN в RNN сложнее, чем в CNN, из-за динамической природы последовательностей и зависимости выходов RNN от предыдущих временных шагов.
— BN для входных весов: Применяется к данным на каждом временном шаге независимо. Это аналогично применению BN в сверточных и полносвязных слоях.
— BN для переходных весов: Сложнее, так как требует расчета статистик BN по всем временным шагам. В некоторых реализациях используется усреднение статистик по временным шагам.
Пару примеров
В сверточной сети с TensorFlow:
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, BatchNormalization, MaxPooling2D, Flatten, Dense
model = Sequential([
Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
BatchNormalization(),
MaxPooling2D((2, 2)),
Conv2D(64, (3, 3), activation='relu'),
BatchNormalization(),
MaxPooling2D((2, 2)),
Flatten(),
Dense(64, activation='relu'),
BatchNormalization(),
Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])Для transfer learning:
from torchvision import models
class TransferLearningModel(nn.Module):
def __init__(self, num_classes):
super(TransferLearningModel, self).__init__()
self.resnet = models.resnet50(pretrained=True)
for param in self.resnet.parameters():
param.requires_grad = False
num_features = self.resnet.fc.in_features
self.resnet.fc = nn.Sequential(
nn.Linear(num_features, 256),
nn.BatchNorm1d(256),
nn.ReLU(),
nn.Linear(256, num_classes)
)
def forward(self, x):
return self.resnet(x)
model = TransferLearningModel(num_classes=10)В рекуррентной сети с PyTorch:
class RNNWithBN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
super(RNNWithBN, self).__init__()
self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
self.bn = nn.BatchNorm1d(num_layers)
def forward(self, x):
x, _ = self.rnn(x)
x = self.bn(x)
return x
model = RNNWithBN(input_size=10, hidden_size=20, num_layers=2)Заключение
Dropout и Batch Normalization помогают моделям учиться более эффективно и быть более устойчивыми к переобучению, что, в свою очередь, приводит к улучшению обобщающей способности и производительности на новых данных.
Спасибо за прочтение статьи, с наступающим новым годом!
Комментарии (2)

Akbari
22.12.2023 11:31Очень хорошая статья. Но в некоторых местах с точки зрение математики и программирование надо делать изменение:
Нормализация:

, где ϵ — маленькое число для избежания деления на ноль.
Тут эпсилон не маленькое число а именно маленький положительной число. Это для того чтобы избежать от деление на ноль(в случай что сигма = ноль).
4. Использование ограничения веса: Веса сети могут увеличиваться в размерах в ответ на вероятностное удаление активаций слоя. Чтобы противодействовать этому, можно наложить ограничение на веса, чтобы норма всех весов в слое была ниже определенного значения.
В некоторых ситуациях при удаление активации слоя веса сети могут уменьшиться в размерах. Это вполне возможно если все веса слоя отрицательные. В этом случай не только сверху надо ограничить а ещё надо ограничить и снизу тоже.


da-nie
Где бы обратный проход нормализации найти в понятном пошаговом виде (не как в википедии - это я сколько не читал, так и не понял). Прямой легко реализуется.А вот обратный...