Гипотеза «чувствительности» ставила в тупик многих выдающихся специалистов по информатике, но её новое доказательство оказалось настолько простым, что один исследователь смог свести его к единственному твиту

Опубликованная этим летом работа ставит точку в почти 30-летней истории гипотезы, касающейся структуры фундаментальных строительных блоков компьютерных схем. Эта гипотеза «чувствительности» годами ставила в тупик многих выдающихся специалистов по информатике, но её новое доказательство оказалось настолько простым, что один исследователь смог свести его к единственному твиту.
«Эта гипотеза была одной из самых раздражающих и позорных открытых задач во всей комбинаторике и теоретической информатике», — писал в своём блоге Скот Ааронсон из Техасского университета в Остине. «Список людей, пытавшихся доказать её, и не сумевших сделать это, представляет собой список самых выдающихся людей в дискретной математике и теоретической информатике», — добавил он в емейле.
Эта гипотеза связана с булевыми функциями — правилами преобразования строк входящих битов (нулей и единиц) в единственный бит. Одно такое правило выдаёт 1, когда все входящие биты равны 1, и 0 в другом случае; другое правило выдаёт 0, если в строке содержится чётное количество единиц, и 1 в другом случае. Каждая компьютерная схема является некоей комбинацией булевых функций, что делает их «строительным материалом всего, что делается в информатике», — сказал Рокко Серведио из Колумбийского университета.
С годами в информатике было разработано много способов измерения сложности заданной булевой функции. Каждая мера использует свой аспект того, как информация входящей строки определяет бит на выходе. К примеру, «чувствительность» булевой функции, грубо говоря, обозначает вероятность того, что перемена единственного бита на входе изменит бит на выходе. А «сложность запроса» подсчитывает, сколько нужно запросить входящих битов для того, чтобы уверенно знать, каков будет выходящий.
Каждая мера даёт свою уникальную точку зрения на структуру булевой функции. Однако специалисты по информатике обнаружили, что практически все эти меры укладываются в универсальную платформу, и что по значению одной из них можно примерно судить о значении других. И только одна мера сложности не укладывалась в эту схему: чувствительность.
В 1992 году Ноам Нисан из Еврейского университета в Иерусалиме и Марио Сегеды, сейчас работающий в университете Рутгерса, предположили, что чувствительность всё же укладывается в эту платформу. Но никто не мог этого доказать. «Этот вопрос, я бы сказал, был выдающимся в области изучения булевых функций», — сказал Серведио.
«Люди писали длинные, сложные работы, пытаясь достичь совсем небольшого прогресса», — сказал Райан О’Доннел из университета Карнеги-Меллон.
А теперь Хао Хуан, математик из университета Эмори, доказал гипотезу чувствительности при помощи гениального, но элементарного доказательства на две странички, связанного с комбинаторикой точек на кубах. «Оно прекрасно, как драгоценная жемчужина», — писала Клэр Мэтью, из французского государственного центра научных исследований в интервью по скайпу.
Ааронсон и О’Доннел назвали работу Хуана «книжным» доказательством гипотезы чувствительности, имея в виду понятие «небесной книги» Пала Эрдёша, в которую Бог записывает идеальные доказательства каждой теоремы. «Мне сложно представить, что даже Богу известно более простое доказательство теоремы чувствительности», — писал Ааронсон.
Чувствительная тема
Представьте, сказала Мэтью, что вы заполняете на бланке для получения займа в банке форму с вопросами, ответы на которые могут быть вида «да/нет». Когда вы закончите, банкир оценит результаты и скажет вам, подходите ли вы для получения займа. Этот процесс является булевой функцией: ваши ответы – это входящие биты, а решение банкира – выходящий.
Если в вашей заявке отказано, вы можете задуматься о том, могли ли вы изменить результат, соврав в одном-единственном вопросе – возможно, заявив, что вы зарабатываете больше $50 000 в год, хотя это не так. Если эта ложь изменит результат рассмотрения, информатики назовут такую булеву функцию «чувствительной» к значению определённого бита. Если, допустим, вы могли бы соврать в одном из семи мест, и каждый раз поменять тем самым результат, тогда чувствительность булевой функции оценки вашей заявки на кредит равняется семи.
Специалисты по информатике определяют общую чувствительность булевой функции как наибольшее значение чувствительности на всех возможных вариантах заполнения заявки. В некотором смысле эта мера подсчитывает, сколько вопросов будут действительно важными в большинстве пограничных случаев – в заявках, результат рассмотрения которых легче всего изменить, если немного изменить сами заявки.
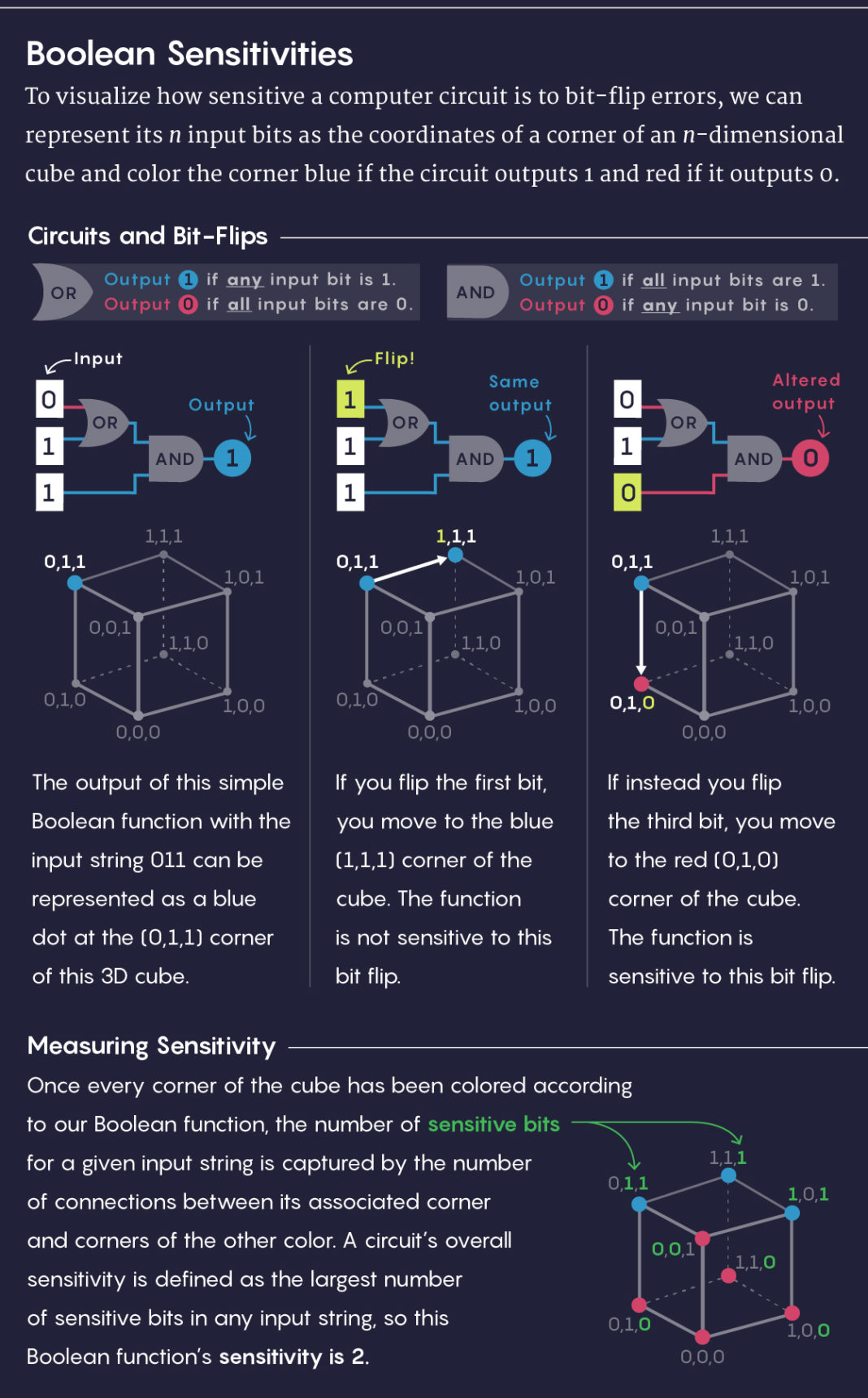
Для визуализации чувствительности контура к ошибкам с обращением битов n входящих битов можно представить в виде координат вершин n-мерного куба. Мы будем окрашивать вершину синим, если контур выдаст 1, и красным – если 0.
В середине слева: выход простой булевой функции со входом 011 можно представить синей точкой на вершине куба (0,1,1).
В центре: Обратив первый бит, мы перейдём в синюю вершину куба (1,1,1). Функция не чувствительна к обращению этого бита.
В середине справа: Обратив третий бит, мы перейдём к красной вершине куба (0,1,0). Функция чувствительна к обращению этого бита.
Раскрасив все вершины куба, мы получим количество чувствительных битов для заданной входящей строки равным количеству связей между соответствующей вершиной и вершинами другого цвета. Чувствительность контура определяется как самое большое количество чувствительных битов в любой входящей строке, поэтому у данной функции чувствительность равна 2.
Чувствительность обычно является одной из самых простых для расчёта мер сложности, однако она вовсе не является простой разъясняющей мерой. К примеру, наш банкир, вместо того, чтобы дать вам бланк на заполнение, мог бы начать с единственного вопроса, а потом использовать ваш ответ, чтобы определить, какой вопрос задать далее. Самое большое количество вопросов, которое может задать банкир перед тем, как прийти к решению, является булевой функцией сложности запроса.
Такая мера появляется в самых разных ситуациях – к примеру, доктор может захотеть отправить пациента на сбор как можно меньшего количества анализов для того, чтобы поставить диагноз, или эксперт по машинному обучению может захотеть создать алгоритм, изучающий как можно меньше свойств объекта перед тем, как тот сможет его правильно классифицировать. «Во многих ситуациях – диагностики или обучения – вам нравится, когда у основного правила низкая сложность запроса», — сказал О’Доннел.
Среди других мер – поиски простейшего способа записать булеву функцию в виде математического выражения, или подсчитать, сколько ответов банкир должен будет показать боссу, чтобы доказать, что заявка была обработана верно. Существует даже вариант сложности запроса из квантовой физики, когда банкир задаёт «суперпозицию» нескольких вопросов одновременно. Разбираясь в том, как эта мера связана с другими мерами сложности, исследователи лучше понимают ограничения квантовых алгоритмов.
Специалисты по информатике доказали существование близкой взаимосвязи всех этих мер, за исключением чувствительности. Конкретнее, они нашли, что они связаны друг с другом полиномиальной зависимостью – к примеру, одна мера может выражаться, как квадрат или куб другой. И только чувствительность упрямо сопротивлялась, не желая встраиваться в эту удобную схему классификации. Многие исследователи подозревали, что она должна к ней подходить, но не могли доказать, что не существует каких-нибудь странных булевых функций, чувствительность которых связана с другими мерами не полиномиальной, а экспоненциальной зависимостью, что в данном случае означало бы, что мера чувствительности кардинально меньше остальных.
«Этот вопрос 30 лет не давал людям спать спокойно», — сказал Ааронсон.
Загоняем решение в угол
Хуан узнал про эту гипотезу в конце 2012 года, за обедом с математиком Майклом Саксом из института передовых исследований, где Хуан был на должности постдока. Его сразу же увлекли простота и элегантность гипотезы. «И с того момента я стал одержим мыслями о ней», — сказал он.
Хуан добавил гипотезу чувствительности в «тайный список» интересовавших его задач, и когда он узнавал о каком-нибудь новом математическом инструменте, он раздумывал, не может ли тот помочь ему. «Каждый раз после публикации очередной работы я возвращался к этой задаче, — сказал он. – Конечно, я выделял время и силы на работу над более реалистичными задачами».

Хао Хуан на недавнем отдыхе в Лиссабоне
Хуан, как и многие в исследовательском сообществе, знал, что гипотезу о чувствительности можно доказать, если математикам удастся доказать другую гипотезу с более простым условием, касающуюся набора точек на кубах различных измерений. Существует естественный способ перехода от строки из нулей и единиц к точке на n-мерном кубе: просто используйте n битов в качестве координат этой точки.
К примеру, четыре двухбитных строки — 00, 01, 10 и 11 – соответствуют четырём углам квадрата на двумерной плоскости: (0,0), (0,1), (1,0) и (1,1). Точно так же восемь трёхбитных строк соответствуют восьми углам трёхмерного куба, и так далее, для более высоких измерений. Булеву функцию можно считать правилом раскраски этих углов кубов двумя разными цветами (допустим, красным для 0 и синим для 1).
В 1992 году Крейг Готсман, сейчас работающий в технологическом институте Нью-Джерси и Нати Линьял из Еврейского университета поняли, что доказательство гипотезы чувствительности можно свести к ответу на простой вопрос о кубах различных измерений: если взять любое множество, состоящее из более чем половины вершин кубов, и раскрасить их в красный цвет, обязательно ли там найдётся красная точка, соединённая со многими другими красными точками (под «соединёнными» точками мы имеем в виду, что две вершины соединены общим ребром, а не расположены по диагонали).
Если в нашем подмножестве содержится ровно половина вершин куба, они могут быть не соединены друг с другом. К примеру, среди восьми углов трёхмерного куба четыре точки,
(0,0,0), (1,1,0), (1,0,1) и (0,1,1), находятся по диагонали друг от друга. Но как только больше половины вершин куба любого измерения окрашиваются в красный цвет, среди них обязательно должны появиться связанные между собой красные точки. Вопрос в том, как распределяются эти связи? Будет ли среди этих вершин хотя бы одна с большим количеством соединений?
В 2013 году Хуан начал думать о том, что лучшим способом понять этот вопрос, возможно, будет использование стандартного метода представления сети при помощи матрицы, отслеживающей, какие из точек связаны между собой, и потом изучающей множество чисел, называющихся собственными значениями матрицы. Пять лет он периодически возвращался к этой идее, но безуспешно. «По крайней мере, благодаря тому, что я о ней думал перед сном, множество ночей мне легче было заснуть», — прокомментировал он запись в блоге Ааронсона.
Затем в 2018 году Хуан подумал об использовании теоремы чередования Коши, математического утверждения 200-летней давности, связывающей собственные значения матрицы с подматрицей, что, возможно, делает её идеальным инструментом для изучения взаимосвязи куба и подмножества его вершин. Хуан решил запросить грант у государственного научного фонда для дальнейшего изучения этой идеи.
Затем в прошлом месяце, сидя в отеле Мадрида и заполняя заявку на грант, он внезапно понял, что может продлить использование этого подхода до самого конца, просто меняя знаки у некоторых чисел из матрицы. Таким способом он смог доказать, что в любом наборе из более чем половины вершин n-мерного куба будет существовать точка, связанная, по меньшей мере, с vn других точек – и из этого результата сразу же вытекает гипотеза чувствительности.
Когда Мэтью получила по почте работу Хуана, первой её реакцией было «ой-ёй-ёй», сказала она. «Когда задача существует 30 лет и все о ней знают, то её доказательство должно быть либо очень длинным и сложным, или очень глубоким». Она открыла файл с работой, ожидая, что ничего не поймёт.
Однако доказательство оказалось достаточно простым для того, чтобы Мэтью и другие исследователи смогли переварить его в один присест. «Думаю, что уже этой осенью его будут рассказывать студентам в рамках одной лекции на каждом курсе магистра по комбинаторике», — написала она в скайпе.
Результат Хуана оказался даже более сильным, чем необходимо для доказательства данной гипотезы, и эта сила должна дать нам новые идеи по поводу мер сложности. «Она добавилась в наш инструментарий, и, возможно, поможет ответить на другие вопросы, связанные с булевыми функциями», — сказал Серведио.
Но главное, что результат Хуана позволяет прекратить все волнения по поводу того, не является ли чувствительность каким-то странным чужаком в мире мер сложности, сказал Серведио. «Думаю, что вечером, узнав об этих результатах, очень многие смогли заснуть спокойно».
Комментарии (53)

arheops
25.09.2019 11:52Обьяснение в виде твита — шикарное.
Это как раз тот момент, когда специалист с профильным университетским дипломом может спокойно признать, что оно выглядит как иностранный язык.

Bookvarenko
25.09.2019 12:12Ну, чтобы понять суть статьи в самом приближённом виде, надо самому попробовать закодить куб и натянуть на его поверхности текстуры скайбокса. Я попробовал. Узнал много нового.

vassabi
25.09.2019 14:08проще говоря — удалось доказать математическую зависимость "меры чуствительности" относительно прочих мер (т.е. "не меньше чем корень" и т.д.) и теперь у математиков будет на одну лекцию больше рассказа для студентов (заодно и мотивация :) "вот видите — как просто, вы тоже можете так, если будете больше думать")

GeMir
25.09.2019 17:27+18гипотеза «чувствительности» ставила в тупик многих выдающихся специалистов по информатике, но её новое доказательство оказалось настолько простым, что один исследователь смог свести его к единственному твиту
Чтобы «статья» была подлиннее, давайте повторим заголовок.
Чтобы «статья» была подлиннее, давайте повторим заголовок.
Fen1kz
25.09.2019 20:21+17Эта статья могла бы быть длиннее, если бы повторяла заголовок — писал в комментариях к этой статье пользователь GeMir с хабрахабра в интернете
В 2019 году GeMir, сейчас находящийся на хабрахабре, предположил, что статья могла бы быть длиннее, если бы повторяла заголовок. «Этот вопрос, я бы сказал, был выдающимся в области написания статей», — сказал GeMir.
«Люди писали длинные, сложные статьи, пытаясь достичь совсем небольшого удлинения», — сказал GeMir с хабрахабра.
Чтобы «статья» была подлиннее, давайте повторим заголовок. — сказал GeMir
Источник- «Эта гипотеза была одной из самых раздражающих и позорных открытых задач во всей комбинаторике и теоретической информатике», — писал в своём блоге Скот Ааронсон из Техасского университета в Остине.
- В 1992 году Ноам Нисан из Еврейского университета в Иерусалиме и Марио Сегеды, сейчас работающий в университете Рутгерса, предположили, что чувствительность всё же укладывается в эту платформу. Но никто не мог этого доказать. «Этот вопрос, я бы сказал, был выдающимся в области изучения булевых функций», — сказал Серведио.
- «Люди писали длинные, сложные работы, пытаясь достичь совсем небольшого прогресса», — сказал Райан О’Доннел из университета Карнеги-Меллон.
- «Этот вопрос 30 лет не давал людям спать спокойно», — сказал Ааронсон.

catharsis
25.09.2019 20:32+1Мне вот что интересно, если не повторяться, то читатели не поймут или за буковки не заплатят?

Barbaresk
25.09.2019 21:59+5А мне вот этот кусок понравился:
Эта гипотеза связана с булевыми функциями — правилами преобразования строк входящих битов (нулей и единиц) в единственный бит. Одно такое правило выдаёт 1, когда все входящие биты равны 1, и 0 в другом случае; другое правило выдаёт 0, если в строке содержится чётное количество единиц, и 1 в другом случае. Каждая компьютерная схема является некоей комбинацией булевых функций, что делает их «строительным материалом всего, что делается в информатике», — сказал Рокко Серведио из Колумбийского университета.
Прям как эталонный студенческий диплом — содержит определения элементарных вещей, пересказанные своими словами, пару ненужных никому примеров и ссылку на бесполезное капитанское утверждение.
Я, даже, не сразу понял, что в этом абзаце написано — пришлось потратить сил, прочитать пару раз, чтобы понять, что никакой ценности абзац не несёт.
Wesha
26.09.2019 07:47Прям как эталонный студенческий диплом.
По-моему, вполне нормально:
Эта гипотеза связана с булевыми функциями — правилами преобразования строк входящих битов (нулей и единиц) в единственный бит.
^ Гипотеза, о которой будут говорить — про хэш-функции (так, MD5 хэширует произвольный файл в набор из 128 бит, а описываемая — в набор, если его так можно назвать, из 1 бита).
Одно такое правило выдаёт 1, когда все входящие биты равны 1, и 0
^ Пример одного из таких алгоритмов
другом случае; другое правило выдаёт 0, если в строке содержится чётное количество единиц, и 1 в другом случае.
^ Пример другого алгоритма того же класса
Каждая компьютерная схема является некоей комбинацией булевых функций, что делает их «строительным материалом всего, что делается в информатике», — сказал Рокко Серведио из Колумбийского университета.
^ А вот это, конечно, хабрааудитории общеизвестно.
P.S. Задумался. Сдаётся мне, функции коррекции ошибок следует искать среди функций с минимальной чувствительностью...

DAleby
26.09.2019 09:32Гипотеза, о которой будут говорить — про хэш-функции
Хэш-функция с двумя значениями? Полезно. Если уж хочется зачем-то дать синоним булевой функции, то это называется «предикат».
Пример одного из таких алгоритмов
Этот «алгоритм» называется AND, конъюнкция
Пример другого алгоритма того же класса
А этот XOR.
То есть, по сути, в том абзаце дается сначала примерное определение булевых функций «на пальцах». Затем приводят два примера: and и xor. А затем следует действительно какое-то капитанское утверждение.
Wesha
26.09.2019 23:04Хэш-функция с двумя значениями? Полезно.
Хэш-функция — это любая функция, (неуникально) отображающая пространство бОльшего размера на пространство меньшего размера. Всё остальное (в том числе и рамзмер пространства) — детали. Случай, когда выходное пространство имеет размер 1 бит — вырожденный, но всё равно легитимный случай.
Этот «алгоритм» называется AND, конъюнкция… А этот XOR.
Несущественные детали. Аффтар всего-навсего приводит примеры. Примеры, как в большинстве случаев, упрощены до невозможности, чтобы понятно было даже самому распоследнему дебилу.
Вы в математику вообще умеете? Там очень многое основывается на предельных случаях (утрируя, "докажем теорему для N участников… рассмотрим случай, когда N=1...") и индукции.

DAleby
27.09.2019 00:05Непонятно, зачем вы пробуете притянуть за уши терминологию, которая не имеет никакого отношения к обсуждаемой теме. Речь конкретно о булевых функциях, это вполне простой и понятный термин.
Хэш-функция — это любая функция, (неуникально) отображающая пространство бОльшего размера на пространство меньшего размер
Я не буду комментировать это определение, только замечу, что булева функция f(b) = b ему не соотвествует.
Вы в математику вообще умеете? Там очень многое основывается на предельных случаях (утрируя, «докажем теорему для N участников… рассмотрим случай, когда N=1...») и индукции.
Ну да, самое удачное место спросить собеседника о том, знает ли он, что такое индукция — это в комментариях к статье о доказательстве математической гипотезы.
Wesha
27.09.2019 00:20Я не буду комментировать это определение
Хеш-функция — функция, осуществляющая преобразование массива входных данных произвольной длины в (выходную) битовую строку установленной длины. В данном случае "установленная длина" = 1 бит.
только замечу, что булева функция f(b) = b ему не соотвествует.
Жду объяснений, как именно не соответствует. Как я уже писал выше, это просто частный случай хеш-функции: из пространства размера X переводит в пространство размера 1. Практическая ценность, конечно, близка к нулю (но выше я уже упоминал, например, коды обнаружения/коррекции ошибок: результат "свёртки" = 0 — ошибки нет, результат 1 = ошибка есть).

VDG
27.09.2019 00:57Хеш-функция — функция, осуществляющая преобразование массива входных данных произвольной длины в (выходную) битовую строку установленной длины.
Можно подать входные данные на набор булевых функций, где каждая функция отвечает за свой выходной бит в выходных данных, и получить таким образом выход любой требуемой разрядности. Или такая «сборка» уже не будет хеш-функцией?
Wesha
27.09.2019 01:21Я не понял, кому Вы это сказали — судя по треду, мне; судя по логике — моему оппоненту. Но я с Вами полностью согласен. (Правда, такие функции могут получиться весьма сложными, но тем не менее принципиально Вы правы. Мы ведь тут не придумываем, как эффективнее функции вычислять, а всего лишь занимаемся интеллектуальным
онанизмомупражнениями.)
VDG
27.09.2019 03:20Мне интересна тема хеш-функций с булевым выходом, поэтому спросил у того, кто видит их связь со статьёй, — у Вас.
Интуитивно предполагаю, что чувствительность у хеш-функций должна быть высокой. То есть, чувствительность можно использовать как оценку «качества» для отбора хеш-функций, порождённых, к примеру, генетическим алгоритмом.
А для перцептивных хешей чувствительность, как мне кажется, должна быть наоборот низкой, чтобы небольшие флуктуации точки в гиперкубе не меняли значение на выходе функции.
Вот хочу спросить, используют ли чувствительность для оценки хеш-функций?
Wesha
27.09.2019 03:37Видите ли, любая функция, осуществляющая вышеописанное отображение, является, по определению, хеш-функцией. А вот является ли она хорошей хеш-функцией — это уже совершенно другой вопрос ;) И моя интуиция с Вашей согласна — (именно для повышения чувствительности в MD5 и прочих алгоритмах применяют неоднократное перемешивание битов). Вот то, что "малое изменение исходного файла вызывает значительное изменение результата" называется "чувствительностью" — это я из этой статьи узнал :)
Вот хочу спросить, используют ли чувствительность для оценки хеш-функций?
Не знаю, но мне кажется, было бы логично так делать!

mayorovp
26.09.2019 09:45Можно было написать академично: "любая булева функция может быть представлена как полином Жегалкина".
Можно написать по-простому: "комбинируя AND и XOR можно составить любое условие".
А можно написать так, как написано в статье — длинно, наукообразно, и запутанно.
А вот это, конечно, хабрааудитории общеизвестно.
Надеюсь, что всё-таки да. Особенно во втором варианте.

Barbaresk
26.09.2019 15:12Если быть совсем точными, то:
«комбинируя AND, XOR, константу 1 можно составить любое условие».
Без константы1 система вроде не полная.
А так да, печальная статья(

rafuck
25.09.2019 23:37Этот аккаунт все время выдает публикации в таком стиле. Я уже даже научился пропускать записи в ленте, не читая заголовок, если вижу характерный аватар. Но бывает (как сейчас, например), что переходишь в статью из «читают сейчас» или «обсуждаемого».

Zalmancheg
26.09.2019 22:01Я не знаю, насколько давно это там началось, но вот буквально на днях дочитал науч-поп книгу "Математика. Утрата определённости" (1980 г.), и там тоже самое — одна и та же мысль по пять раз (раза 3 в пределах нескольких страниц после первого упоминания и потом еще парочку дальше по тексту) и куча воды…

Magister-Ice
25.09.2019 21:32А нельзя ли было кратко и по сути, первые 9 абзацев вообще не несут никакой смысловой нагрузки (их можно было бы смело вынести в конец статьи).

knowy
26.09.2019 03:39+1Легко: видим автора, плашку «Перевод», проходим мимо.
Если совсем нечего делать и нет свежих статей — пробегаем текст глазами в течение 10 секунд и пытаемся найти что-то интересное, а потом проходим мимо.
pehat
26.09.2019 03:53Эм. Самое интересное в статье находится по клику на ссылку «Автор оригинала».

knowy
26.09.2019 04:12Действительно. Вношу поправку:
Если совсем нечего делать — пробегая глазами, мотаем до низа и кликаем на оригинал. Но там тоже сильно не факт, что будет интересно. Ув. SLY_Gиногдапериодически ошибается при переводе каких-то технических деталей, но суть обычно передает верно, и океаны воды в статьях — не его вина.
И интересные статьи он тоже переводит. Чего стоит первая половина цикла «Спросите Итана».

perfect_genius
25.09.2019 21:36Если я правильно понял, дендриты в мозге тоже ведь так работают, как на первой анимированной гифке? В итоге выход — нейрон пускает-таки импульс в аксон к дендритам следующего нейрона.
Т.е. это доказательство может оказаться полезным в понимании работы мозга.
VDG
26.09.2019 01:08Для дендритной (к примеру, базальной) ветки, чтобы она сработала должна активироваться цепочка синапсов. Похоже как на гифке, но она просто приведена как пример некой сложной булевой функции, полученной как комбинация нескольких простых.
Ну и к тому же на дендритную ветку «проецируется» только одна вершина гиперкуба, а в статье оперируют множеством вершин.
perfect_genius
26.09.2019 21:31Кстати, вот эти ребята снизу справа особенно походят:


VDG
27.09.2019 00:18Не, эти не подходят. Это клетки Пуркинье, у них специфическая функция, насколько помню, им нужно заметить вообще любую активность. А я говорил о базальных дендритных ветках пирамидальных нейронов, вон они торчат в стороны из тела нейрона, который слева внизу.

perfect_genius
27.09.2019 21:15Замечают любую активность, быстро доставляют сигнал нейрону и он тоже сразу пускает сигнал в аксон?

Biga
25.09.2019 21:58Мало чего понял, но хотя бы могу уснуть спокойно.

KirillGerasimov
25.09.2019 22:37+7Прошу прощения у математиков, постарался убрать все математические термины из объяснения.
Что такое чувствительность функции на пальцахЕсть функция от нескольких булевых аргументов. Для примера пусть их будет 5. Мы хотим измерить ее чувствительность. Возьмем любой произвольный вход
f(0,1,0,1,1) = 1
каждый аргумент по очереди меняем 0 -> 1, 1 -> 0
f(1,1,0,1,1) = 1 f(0,0,0,1,1) = 0 f(0,1,1,1,1) = 1 f(0,1,0,0,1) = 1 f(0,1,0,1,0) = 0
Смотрим, что функция поменяла свое значение с 1 на 0 для двух вариантов. Значит "чувствительность" этого входа 2.
Для того чтобы узнать чувствительность функции, нам нужно пробежать по каждому возможному входу (в этом случае их 2^5) и выбрать максимальную чувствительность.
Т.е. если мы найдем вход, чувствительность которого будет 3, но не сможем найти вход с чувствительностью 4. То результирующая чувствительность булевой функции будет равна 3.

lagranzh
26.09.2019 00:52+1спасибо, а то у меня глаза сломались после третьего абзаца. Что такое чувствительность, теперь понятно. А в чем была гипотеза?

CryptoPirate
26.09.2019 11:15Если я правильно понял, гипотеза в том что чувствительность такой функции с n аргументами больше или равна sqrt(n) в виде формулы:
Чувстветельность(f_n) >= sqrt(n)
lagranzh
26.09.2019 11:55что-то не то. если функция — константа, то чуствительность 0. Если функция это 'xor', то чуствительность 'n'.

fingolfin
25.09.2019 23:42+6Статья — сплошная вода. Где само доказательство? Как оно работает? Единственное, что здесь было интересного — картинка с кубом — осталось непереведённым.

mayorovp
26.09.2019 09:48Доказательство как раз есть, в твите после третьего абзаца. Мне больше интересно какая именно теорема доказывалась, без этого ничего понять не получается.

Sistemaalex
26.09.2019 08:31+1Ссылка на ученого Hao Huang www.mathcs.emory.edu/~hhuan30
Ссылка на доказательство www.mathcs.emory.edu/~hhuan30/papers/sensitivity_1.pdf

Sistemaalex
26.09.2019 08:39Спасибо Вам за вашу работу. Просто по Вашим переводам очень часто понятно, чем они, на западе заморочены, и с какими проблемами работают и на каком уровне.

skvoo
26.09.2019 12:00Это уже давно было решено, просто забыли всем рассказать

bodqhrohro
26.09.2019 21:05Учёный из Венесуэлы придумал поистине замечательное доказательство, но у него не хватило бумаги, чтобы его записать :->

frkbvfnjh
26.09.2019 12:00А зачем вообще нужно понятие чувствительности, где это можно применить, какого черта вообще придумали эту гипотезу?

DrAlan
26.09.2019 12:43Ну в статье это раскрывается косвенно. Если прикинуть с высоты обывателя (то есть то что можем сделать я и любой другой кто не ленится) очевидно что первое применение это стоит ли проводить оценку входных данных порционно (высокая чувствительность) или необходимы все данные за раз (низкая). Был описан пример нейронных сетей например.

ArcadijVK3
27.09.2019 17:31-1Повторю, это — чушь. в булевой алгебре нет понятия чувствительности, вероятности, и прочее. У булевых функций, может быть много аргументов, но все они или 0, или 1, все!!! это закон. Если какой то то ученый утверждает, что 0, может стать, 1, тут ему нужно заняться другим понятием — передача данных с искажениями информации. и восстановлением ее. И еще, когда в статье, или как у вас пишут посте, банкир оперирует понятиями квантовой механики(суперпозицией, или задать сразу несколько вопросов, ну чушь), попридержи коней, не могут они этого знать, по определению. Банкир, человек, который по определению, не может знать теории квантовой физики. Сам прочти, и не переводи больше, не надо.


Snow_Bars
В чем суть статьи-то? Пространные разговоры вокруг темы?
ofigenn
Матан!
makondo
скорее дискретный анализ…
mayorovp
Где?!
AVI-crak
Способ натянуть менеджера банка на все грани кубика с помощью булевых операций.
Сделать это так, чтобы он ничего не почувствовал.
KirillGerasimov
Насколько я понял суть гипотезы в том, что для n-мерного входа, чувствительность булевой функции по крайней мере корень из n , но повторяющиеся тезисы в статье и бессмысленные в ставки мешают понять это.
Что такое чувствительность
Starche
Если я вас правильно понял, то немного не совсем так. Не от входа корень считается, потому что например функция-константа имеет размер входа n, но чувствительность ноль.
Правильная формулировка такая: чувствительность не меньше корня из deg(f) (степени функции).
А что такое степень надо говорить отдельно.
Любую булеву функцию можно представить в виде полинома. Я не уверен, что прав, но вроде бы имеется в виду Полином Жегалкина. Собственно deg(f), т.е. степень функции — это степень этого полинома, т.е. максимальная степень его слагаемых.
Вообще парень доказал штуку, которая довольно просто формулируется в терминах графов. В n-мерном кубическом графе любой подграф степени 2^(n-1)+1 (т.е. имеющий больше половины вершин исходного графа) имеет вершину степени не меньше чем sqrt(n).
Правда я понятия не имею, как из этой теоремы следует теорема чувствительности, но вроде как это известный переход, на который ссылается автор. Только разобраться надо.
Starche
Нашёл статью 1992-го года, в которой описывается эквивалентность утверждений про кубический граф и про чувствительность функции www.sciencedirect.com/science/article/pii/0097316592900608
Там ещё пара страниц доказательства, которые я пожалуй пока не осилю)