Законы физики не меняются от смены точки зрения. Однако эта идея помогает компьютерам распознавать определённые особенности в искривлённом пространстве высших измерений.

Компьютеры учатся водить автомобили, обыгрывают чемпионов мира в настольные игры, и даже пишут прозу. По большей части революция ИИ зиждется на возможностях одного типа искусственной нейронной сети, схема работы которой вдохновлена связанными друг с другом слоями нейронов в зрительной коре мозга млекопитающих. Так называемые «свёрточные нейронные сети» (СНС) оказались удивительно хорошо приспособленными к поиску закономерностей в двумерных данных – особенно в таких задачах компьютерного зрения, как распознавание рукописных слов или объектов на цифровых изображениях.

Но в применении к наборам данных, не сводимых к геометрии на плоскости – к примеру, к моделям неправильных форм, используемых в трёхмерной компьютерной анимации, к облакам точек, генерируемых робомобилями для разметки окружающего их мира – эта эффективная архитектура машинного обучения (МО) уже не так хорошо работает. В 2016 году появилась новая дисциплина, геометрическое глубокое обучение (ГГО), целью которой стало вывести СНС за пределы плоскости.

Теперь исследователи достигли своей цели, разработав новую теоретическую платформу для построения НС, способных находить закономерности на любых геометрических поверхностях. Эти калибровочно эквивариантные свёрточные нейросети (КЭСНС) [gauge-equivariant convolutional neural networks] были разработаны в Амстердамском университете и лаборатории исследований ИИ Qualcomm при участии таких исследователей, как Тако Коэн, Морис Вейлер, Беркай Кицаноглу и Макс Веллинг. ЭСНС могут находить закономерности не только в двумерных массивах пикселей, но и на сферах и на асимметрично искривлённых объектах. «Эта платформа – определённый ответ на вызов, брошенный проблемой глубокого обучения на искривлённых поверхностях», — сказал Веллинг.

КЭСНС уже серьёзно обогнали своих предшественников в деле обнаружения закономерностей в симуляциях глобального климата, которые естественным образом ведутся на сфере. Алгоритмы также могут оказаться полезными для улучшения зрения дронов и робомобилей, воспринимающих трёхмерные объекты, и для обнаружения закономерностей в данных, собранных с искривлённых поверхностей неправильной формы сердца, мозга или других органов.


Тако Коэн, один из ведущих архитекторов КЭСНС

Найденное исследователями решение проблемы ГО за пределами плоскости имеет глубокую связь с физикой. Описывающие мир физические теории, типа ОТО Альберта Эйнштейна или Стандартной Модели в физике имеют свойство «калибровочной эквивариантности». Это значит, что величины мира и их взаимосвязь не зависит от произвольных систем отсчёта (или «калибровки»); они остаются неизменными вне зависимости от того, движется наблюдатель или покоится, или от расстояния между числами на линейке. Измерения, сделанные разными средствами, должны конвертироваться друг в друга так, чтобы сохранять взаимосвязь между вещами.

К примеру, если мы измерим длину футбольного поля в ярдах, а потом в метрах, то получим разные цифры, однако их отличие будет предсказуемым. Два фотографа, делающих снимки объекта с двух разных точек, получат разные изображения, но их можно связать друг с другом. Калибровочная эквивариантность гарантирует непротиворечивость физических моделей вне зависимости от точки зрения или единиц измерения. КЭСНС принимают те же предположения касательно данных.

«Они хотели привнести в нейросети идею из физики – когда не существует каких-либо выделенных направлений, — сказал Кайл Кранмер, физик из Нью-Йоркского университета, применяющий МО к физике частиц. — И придумали, как это сделать».

Побег с плоскости

Майкл Бронштейн, специалист по информатике из Имперского колледжа Лондона, в 2015 году придумал термин «геометрическое глубинное обучение» для описания впервые делавшихся тогда попыток уйти от плоскости и разработать НС, способные искать закономерности в трёхмерных данных. Вскоре этот термин – и исследования – прижились.

Бронштейн с соратниками знали, что выход за евклидовую плоскость потребует заново придумать одну из базовых вычислительных процедур, делающих НС такими эффективными в распознавании двумерных изображений. Эта процедура, т.н. «свёртка», позволяет слою НС проводить математическую операцию на небольших участках входных данных, а потом передавать полученный результат следующему слою сети.

«Свёртку можно представить себе примерно как сдвигающееся окно», — пояснил Бронштейн. СНС двигает много таких окошек-фильтров по данным, причём каждое из них ищет определённую закономерность. В случае фото кота обученная СНС может использовать фильтры, распознающие в пикселях признаки низкого уровня, такие, как грани. Эти признаки передаются вверх на следующие слои сети, и те проводят дополнительные свёртки, выбирая признаки более высокого уровня – такие, как глаза, хвост или треугольные уши. В итоге обученная распознавать котов СНС использует результаты этих послойно полученных свёрток для того, чтобы отметить, есть на фото кот или нет.


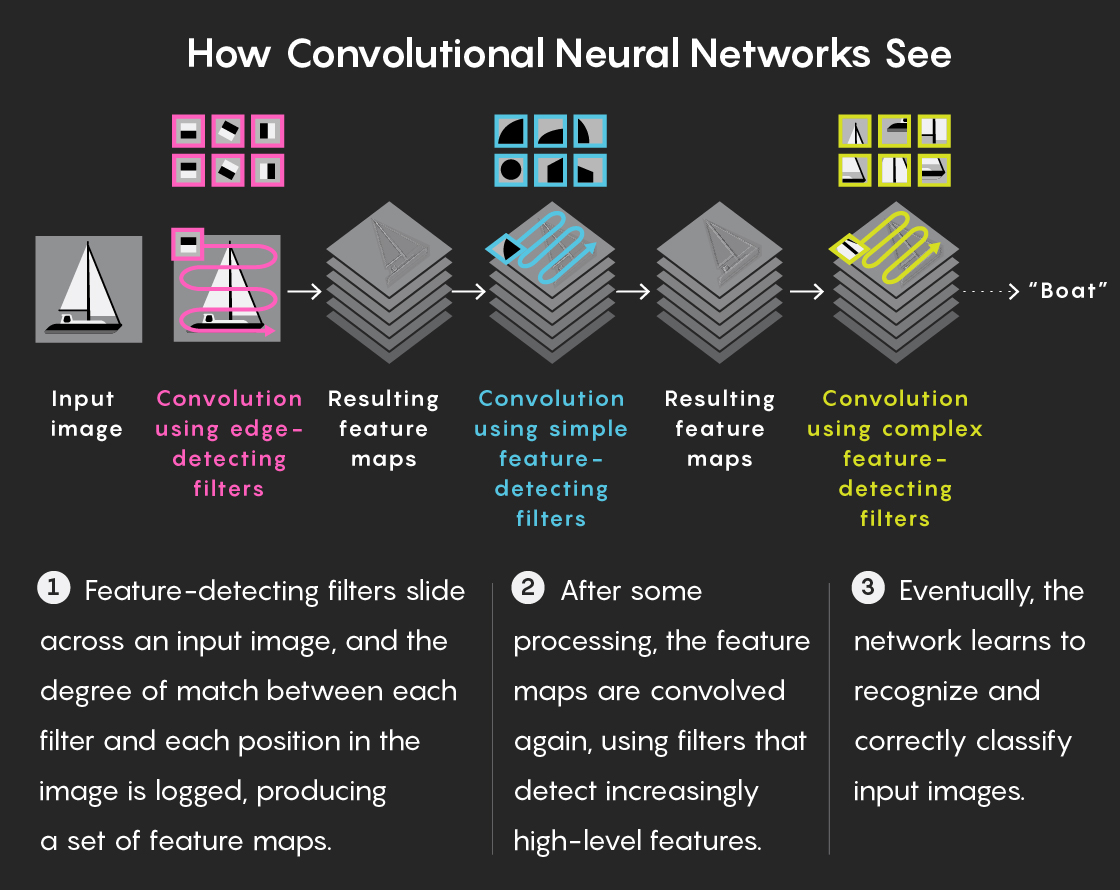
Как видят СНС:

1. Фильтры, распознающие признаки, двигаются по входящему изображению, и степень совпадения с каждым фильтром на каждой позиции записываются, что даёт карту признаков.
2. После обработки карты признаков вновь подвергаются свёртке, уже с использованием фильтров, настроенных на признаки более высокого уровня.
3. В итоге сеть обучается распознавать и правильно классифицировать изображения.

Однако такой подход работает только на плоскости. «Когда плоскость, на которой вам нужно проводить анализ, искривляется, у вас появляются проблемы», — сказал Веллинг.

Проводить свёртку на искривлённой поверхности – в геометрии это называется топологическим многообразием – всё равно, что прижимать квадратный кусочек миллиметровой бумаги к глобусу, пытаясь точно перенести на неё контуры побережья Гренландии. Нельзя прижать к Гренландии бумагу, не смяв её, а значит, ваш рисунок получится искажённым, когда вы его снова разгладите. Можно прислонить бумагу к глобусу в одной точке, и рисовать контуры, глядя на них сквозь бумагу (эта техника известна под названием проекция Меркатора), однако искажения получатся и в этом случае. Можно приложить миллиметровку к плоской карте мира, а не глобусу, но тогда вы просто будете копировать её искажения – к примеру, задумайтесь о том, что весь верхний край карты на самом деле обозначает единственную точку на глобусе, Северный полюс. А если многообразие окажется не аккуратной сферой типа глобуса, но чем-то более сложным и неправильным, вроде трёхмерной формы бутылки, или уложенного белка, то проводить на нём свёртку будет ещё сложнее.

Бронштейн с коллегами обнаружили одно решение проблемы свёртки на неевклидовых многообразиях в 2015 году. Они заменили скользящее на окно на конструкцию, больше напоминающую круглую паутину, нежели кусочек миллиметровки – её можно прислонить к глобусу (или любой искривлённой поверхности), не сминая, не разрывая и не растягивая.

Изменение свойств скользящего фильтра благоприятным образом сказалось на понимании СНС определённых геометрических взаимосвязей. К примеру, сеть могла автоматически понимать, что трёхмерная фигура, изогнутая разными способами – допустим, человек, стоящий прямо, и человек, поднявший одну ногу – это один и тот же объект, а не два совершенно разных. Также это изменение кардинально улучшило показатели обучения НС. Стандартные СНС «использовали миллионы примеров фигур, их требовалось обучать неделями, — сказал Бронштейн. – Мы используем порядка 100 фигур в разных позах и обучаем сеть где-то полчаса».

В то же время, Тако Коэн и его коллеги из Амстердама начали подходить к этой проблеме с противоположной стороны. В 2015 году Коэн, который тогда был аспирантом, не занимался изучением вопроса побега с плоскости. Его интересовала практическая, как он считал, инженерная проблема: эффективность данных, то есть, вопрос о том, как обучать НС при помощи меньшего количества примеров, вместо тех тысяч или миллионов, которые обычно требуются для этого. «Глубокое обучение учится очень медленно», — сказал Коэн. Это не создаёт особых проблем, если вы обучаете СНС распознаванию котов (учитывая неиссякаемый запас фоток котиков в интернете). Но если вы обучаете СНС распознавать что-то более важное, типа раковых опухолей в снимке ткани лёгких, тогда найти достаточное количество обучающих данных – точных с медицинской точки зрения, правильно размеченных, свободных от копирайта – довольно сложно. И чем меньше примеров потребуется для обучения сети, тем лучше.

Коэн знал, что один из способов увеличить эффективность данных – дать НС некое представление об этих данных заранее, например, что раковая опухоль лёгкого не перестаёт быть опухолью, если её изображение повернуть или зеркально отразить. Свёрточная сеть обычно должна обучаться такой информации с нуля, изучая множество примеров одной и той же закономерности, подаваемой в разных видах. В 2016 году Коэн и Веллинг вместе работали над статьёй, описывающей, как закодировать некоторые из этих предположений в НС в виде геометрических симметрий. Такой подход настолько хорошо сработал, что в 2018-м Коэн и Марисия Уинклс обобщили его ещё сильнее, продемонстрировав многообещающие результаты в распознавании рака лёгких на КТ-снимках. Их НС смогла найти визуальные свидетельства наличия болезни при помощи всего десятой доли данных, по которым обучались другие нейросети.

Исследователи из Амстердама продолжали свои обобщения, и в итоге пришли к калибровочной эквивариантности.

Расширяя эквивариантность

У физики и машинного обучения есть нечто общее. Как говорит Коэн, «обе области заняты наблюдениями и построением моделей, предсказывающих результаты последующих наблюдений». Что важно, по его словам, так это то, что обе области строят модели не отдельных вещей (вряд ли полезно иметь одно описание для атома водорода, и второе – для такого же атома, только перевёрнутого), но общих категорий. «И физика, конечно же, достигла в этом больших успехов».

Эквивариантность

Эквивариантность (или «ковариантность», как предпочитают физики) – это предположение, на которое физики полагались в обобщении своих моделей со времён Эйнштейна. «Это просто значит, что если вы правильно описываете какую-то физику, тогда это описание должно быть независимо от того, какие ’линейки’ вы используете, или, в общем случае, какой вы наблюдатель», — пояснила Миранда Чен, физик-теоретик из Амстердамского университета, написавшая с Коэном и другими учёными статью по исследованию связей между физикой и КЭСНС. Как писал сам Эйнштейн в 1916: «Общие законы природы должны выражаться уравнениями, работающими во всех системах координат».


Миранда Чен, физик-теоретик из Амстердамского университета

Свёрточные нейросети стали одним из самых успешных методов в ГО благодаря использования простого примера такого принципа, «эквивариантности переноса». Окно-фильтр, распознающее определённый признак в изображении – допустим, вертикальные грани – скользит (или «переносится») по плоскости из пикселей и записывает все места, где находятся такие вертикальные грани; затем оно создаёт «карту признаков», отмечая эти места, и передаёт её в следующий уровень сети. Создавать карты признаков получается благодаря эквивариантности переноса: нейросеть предполагает, что один и тот же признак может появиться в любом месте двумерной плоскости, и что она может распознать вертикальную грань, находись она в правом верхнем или левом нижнем углу.

«Суть эквивариантных НС – взять эти очевидные симметрии и включить их в архитектуру сети, чтобы это свойство отрабатывало как бы бесплатно», — сказала Вейлер.

К 2018 году Вейлер, Коэн и их научный руководитель Макс Веллинг расширили это «бесплатное действие», чтобы в него входили и другие типы эквивариантности. Их «групп-эквивариантные СНС» могут распознавать повёрнутые или отражённые признаки на плоских картинках без необходимости обучаться на конкретных вариантах этих признаков; сферические СНС могут создавать карты признаков на основе данных, расположенных на поверхности сферы, не искажая их при превращении в плоские проекции.

Такой подход всё ещё был недостаточно универсальным для того, чтобы работать с данными на бугристой структуре неправильной формы – то есть, практически на любом объекте реального мира, от картошки до белков, от человеческого тела до кривизны пространства-времени. У подобных многообразий нет «глобальной» симметрии, по поводу которой НС могла бы высказать эквивариантные предположения: любой их участок отличается от всех остальных.


Свёртка на искривлённых поверхностях, на которых не работают стандартные СНС. Фильтр с определением края, скользящий по такой поверхности, в зависимости от пути может принимать разную ориентацию, и выдавать разные карты признаков.

Проблема в том, что скольжение плоского фильтра по поверхности может менять его ориентацию, в зависимости от конкретного пути. Представьте себе фильтр, настроенный на распознавание простого узора: тёмного пятна слева и светлого пятна справа. Поводите его по плоской поверхности во все четыре стороны, и он всегда будет ориентирован одинаково. Но ситуация меняется даже на поверхности сферы. Если провести фильтр на 180 градусов по экватору сферы, его ориентация сохранится – тёмное пятно слева, светлое – справа. Однако если провести его в ту же точку через северный полюс сферы, фильтр окажется перевёрнутым. Он не найдёт тот же самый узор в данных, не выдаст ту же карту признаков. Подвигайте фильтр по более сложному многообразию, и в итоге он сможет указывать в какую угодно сторону.

Суть, как объяснил Веллинг, состоит в том, чтобы забыть об отслеживании изменений ориентации фильтра при движении по разным путям. Вместо этого можно выбрать только одну ориентацию (или калибровку) фильтра, а потом определить непротиворечивый способ преобразовывать в неё любую другую ориентацию.

Проблема в том, что хотя в изначальной ориентации можно использовать любую калибровку, преобразование в другие варианты должно сохранять первоначальную закономерность – так же, как преобразование скорости света из метров в секунду в мили в час должно сохранять лежащую в основе физическую величину. С калибровочно эквивариантным подходом, говорит Веллинг, «сами цифры меняются, но меняются совершенно предсказуемо».

Соэн, Вейлер и Веллинг закодировали калибровочно эквивариантность – тот самый «бесплатный обед» – в свою СНС в 2019-м. Для этого они наложили математические ограничения на то, что НС может «видеть» в данных при применении свёрток; через слои сети проходили только калибровочно эквивариантные закономерности. «По сути, ей можно дать любую поверхность» – от евклидовых плоскостей до произвольно изогнутых объектов, включая такие экзотические многообразия, как бутылка Клейна или четырёхмерное пространство-время – «и она справится с ГО на этой поверхности», — сказал Велинг.

Рабочая теория

Теория КЭСНС настолько обобщена, что автоматически включает предположения из предыдущих геометрических подходов к ГО – к примеру, вращательной эквивариантности или перемещению фильтров по сферам. В неё укладывается даже более ранний метод Майкла Бронштейна, позволявший НС распознавать одну трёхмерную фигуру, изогнутую разными способами. «Калибровочная эквивариантность – очень широкая платформа. В неё в качестве частного случая входит то, что мы делали в 2015-м», — сказал Бронштейн.

КЭСНС теоретически сработает на любой искривлённой поверхности любой размерности, но Коэн и его соавторы проверили её на данных глобального климата, структура которых сферична. Они использовали свою платформу для создания СНС, распознающей экстремальные погодные закономерности, типа тропических циклонов, на основе данных о симуляции климата. В 2017 году правительство и учёные использовали стандартную СНС для определения наличия в данных циклонов с точностью в 74%; в прошлом году КЭСНС распознала циклоны с точностью в 97,9% (она также обогнала менее обобщённый подход к ГО, разработанный в 2018 году специально для сфер – результат у той системы был 94%).

Майюр Мудигонда, климатолог из Национальной лаборатории Лоуренса Беркли, использующий в работе ГО, сказал, что будет продолжать следить за развитием КЭСНС. «Этот аспект человеческого интеллекта, — правильное распознавание признаков вне зависимости от их ориентации в пространстве, — мы и хотим перенести в климатическое сообщество», — сказал он. Компания-производитель чипов Qualcomm, нанявшая недавно Коэна и Веллинга, и купившая основанный ими стартап, планирует применить теорию КЭСНС к разработке улучшенных алгоритмов компьютерного зрения, к примеру, дрона, способного видеть на все 360 градусов сразу (такой вид на мир в стиле «рыбий глаз» естественным образом отображается на сферу, как и данные по глобальному климату).

Тем временем КЭСНС набирают популярность у физиков – к примеру, Кранмер планирует заставить их работать с данными симуляций взаимодействия субатомных частиц. «Мы анализируем данные, связанные с сильным ядерным взаимодействием, пытаясь понять, что происходит внутри протона», — сказал Кранмер. Он сказал, что данные четырёхмерные, «поэтому у нас есть идеальный вариант применения НС имеющих калибровочную эквивариантность».

Ризи Кондор, бывший физик, изучающий теперь КЭСНС, сказал, что потенциальные научные применения таких сетей гораздо важнее, чем их использование в области ИИ. «Если вы занимаетесь распознаванием кошек на YouTube, и обнаруживаете, что плохо распознаёте перевёрнутых вверх ногами кошек, это не очень хорошо, но, возможно, не смертельно», — сказал он. Однако физикам крайне важно, чтобы сеть не распознала поле или траекторию частицы неправильно из-за того, как они были ориентированы. «Это не вопрос удобства, — сказал Кондор, — очень важно с уважением отнестись к имеющимся симметриям».

Однако хотя вдохновением для создания КЭСНС послужила математика, пришедшая из физики, и физикам они могут пригодиться, Коэн отметил, что эти НС не смогут открывать новую физику самостоятельно. «У нас теперь получается создавать сети, способные обрабатывать весьма экзотические данные, однако структуру этих данных нужно знать заранее», — сказал он. Иначе говоря, физики могут использовать КЭСНС потому, что Эйнштейн уже доказал, что пространство-время можно представить в виде четырёхмерного искривлённого многообразия. НС Коэна не смогла бы «найти» эту структуру самостоятельно. «Мы не занимаемся поиском информации о симметриях», — сказал он, хотя он надеется, что в будущем это станет возможным.

Коэн не может нарадоваться существующим между разным областями связям, о которых он раньше лишь предполагал, а теперь продемонстрировал с математической строгостью. «У меня всегда было такое чувство, что машинное обучение и физика занимаются чем-то очень похожим, — сказал он. – Это одно из тех чудес, которым я поражаюсь: мы начали с инженерной проблемы, и в процессе улучшения систем раскрывали всё больше и больше связей».