Популярные функции для создания реалистичных анимаций.

Мы продолжаем цикл статей про математику и смежные дисциплины в компьютерной графике по курсу Александра Паничева, ведущего разработчика логики в UNIGINE. В этот раз поговорим о функциях плавности, которые используются в анимации (и не только).

Простейший пример

Представим ситуацию, что у нас есть машинка и ее нужно анимировать, чтобы она ездила от одного края экрана до другого и обратно.

 Дизайнер: «Надо бы анимировать эту машинку!»   

А теперь представим абстрактного программиста-джуна, который ничего не понимает и решает просто использовать функцию lerp (линейную интерполяцию). Получается нереалистично (1-я анимация ниже), и это замечает Дизайнер, который говорит программисту, что машинка должна в начале разгоняться, а в конце замедляться (2-я анимация ниже):

То есть нужно нелинейное движение (как это обычно и происходит в жизни). При этом, в следующий раз Дизайнер вообще может сказать, что она должна начать ускоряться с 5-й секунды или ехать не более 3 секунд… Можно, конечно, использовать какие-нибудь функции из физики:

С ускорением машины все просто, но как применить эти функции, чтобы машина замедлялась ближе к концу и не проехала дальше нужного?

Опытный программист сразу вспомнит про кривые. Например, про так называемую кривую Безье:

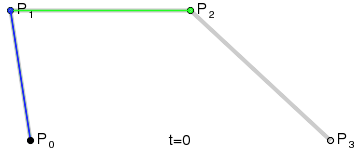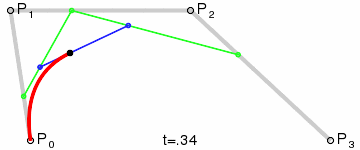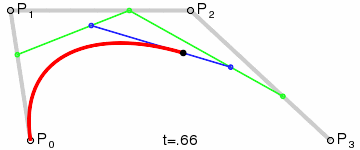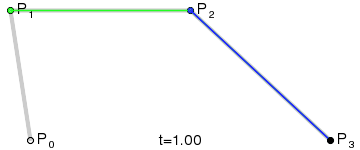
В интерактивных приложениях мы часто сталкиваемся с двумя видами кривых Безье: квадратичной и кубической.

1D Quadratic Bezier (квадратичная кривая Безье)

float bezier_quad(float p0, float p1, float p2, float t)
{
	float it = 1.0f - t;
	return p0 * (it * it) +
		p1 * (2.0f * it * t) +
		p2 * (t * t);
}

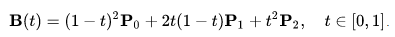
Если воспринимать параметр t за нормализованное время (от 0 до 1), p0 — начальная позиция автомобиля, p2 — конечное, а возвращаемое значение — за текущую позицию автомобиля для текущего времени t, то становится понятно, что, управляя параметром p1 (так называемой контрольной точкой или касательной) мы можем двигать автомобиль либо линейно (p1 между p0 и p2), либо с ускорением (p1 ближе к p0), либо с торможением (p1 ближе к p2).

А как сделать плавное ускорение в начале и плавное торможение в конце?

1D Cubic Bezier (кубическая кривая Безье)

float bezier_cubic(float p0, float p1, float p2, float p3, float t)
{
	float tt = t * t;
	float it = 1.0f - t;
	float itt = it * it;
	return p0 * (itt * it) +
		p1 * (3.0f * itt * t) +
		p2 * (3.0f * it * tt) +
		p3 * (tt * t);
}

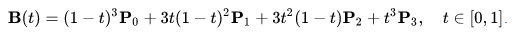
Здесь у нас уже есть целых две контрольных точки! Первое для первой половины анимации и второе для второй половины.

Можно вызвать bezier_cubic(0, 0, 1, 1, t) и увидеть, что анимация у нас стала той, какую мы хотели видеть.

Ну... Почти. С одномерной кубической Безье невозможно контролировать степень искажения, нельзя сделать ускорение и/или торможение еще более сильным.

Что делать? Можно сделать поверх текущей кривой вторую, которая будет искажать t (таким образом и работают кривые в катсцен-редакторах)... Но посмотрите на сложность функции: здесь используется 12 умножений, 3 сложения, 1 вычитание и 5 аргументов на входе. Нельзя ли как-то... попроще? И чтобы контроля было больше. Чтобы можно было сильнее изгибать кривую.

Конечно можно! Ведь для этого и существуют «функции плавности»!

Функции плавности (Easing Functions) Роберта Пеннера

Такого рода анимации, как описанные выше на примере с машинкой, называют Duration-based. У нас есть начало, есть конец и есть продолжительность.

Линейное движение — это использование функции lerp(), она же линейная интерполяция. Она есть в любых игровых движках.

Нелинейное движение — это использование easing-функций (или функций плавности). Они уже встречаются в движках заметно реже. Например, в движке Unity есть сторонний плагин iTween — он уже много лет в топе по скачиваниям.

Помимо разработчиков игровых движков, функциями плавности пользуются веб-дизайнеры и аниматоры.

Функции плавности придумал Роберт Пеннер — математик, физик и Flash-разработчик. Его раздражало, что во Flash сглаженная интерполяция работала либо на ускорение (Ease от -100 до 0, In), либо на торможение (Ease от 0 до 100, Out). Прямо, как с квадратичной кривой Безье. Из-за этого для создания того примера с разгоняющейся в начале и замедляющейся в конце машинкой приходилось использовать дополнительные ключевые кадры.

Всего Роберт изобрел 30 функций:

Кажется, что много, но их можно разделить на 3 категории: In (ускоряющие), Out (затухающие) и InOut (ускорение с затуханием в конце):

Рассмотрим самую первую функцию easeInQuad. Выглядит она так:

float easeInQuad(float t)
{
	return t * t;
}

t — это нормализованное время от 0 до 1 (прямо, как в lerp). Выходящее значение — полученная кривая, также в пределах от 0 до 1 (но есть и исключения, например easeOutElastic).

Как можно понять, Quad тут написано не просто так: аргумент t мы возводим в квадрат. Последующие три функции Cubic, Quart, Quint делают, соответственно, похожую вещь.

Если линейная интерполяция в данном случае — это return t, то остальные варианты — это различные степени t: 3-я, 4-ая, 5-ая. Это и дает изгиб линии — чем выше степень, тем сильнее:

Следующие — Sine, Expo и Circ — это синус/косинус, возведение в степень и движение по окружности соответственно.

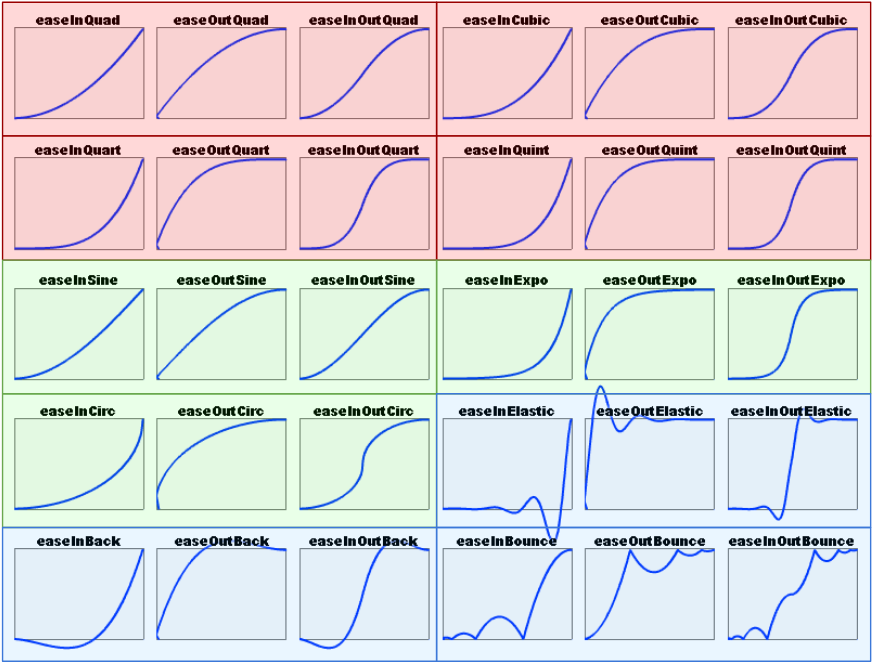
Последняя группа — самые необычные и часто используемые: Elastic (пружина), InBack / OutBack (уход за границу значений от 0 до 1), Bounce (скачки мяча и т.п.).

Функции плавности — это необязательно только положение или смещение. Это также может быть масштаб, поворот, изменение цвета и даже искажение времени — все, что имеет движение можно помножить на эти функции плавности.

EaseInQuad, EaseOutQuad, EaseInOutQuad

На примере анимации движения, вращения и масштабирования easeInQuad() выглядит так:

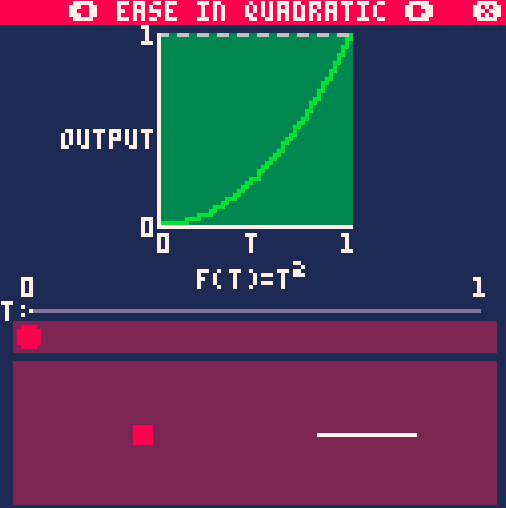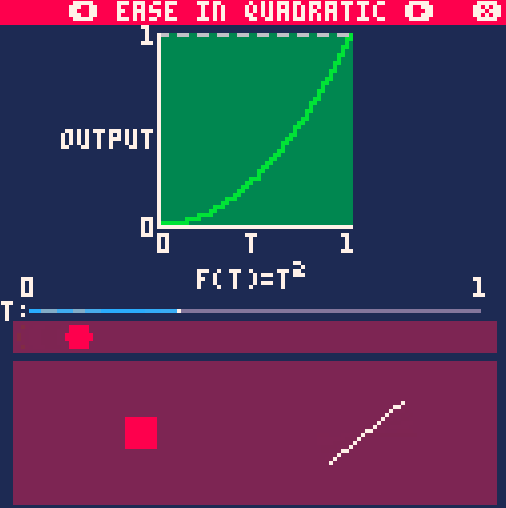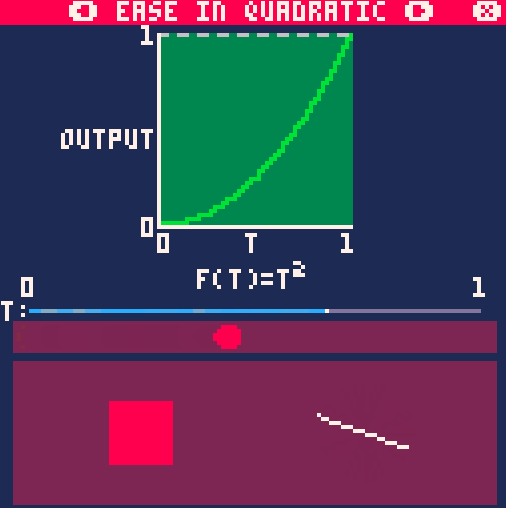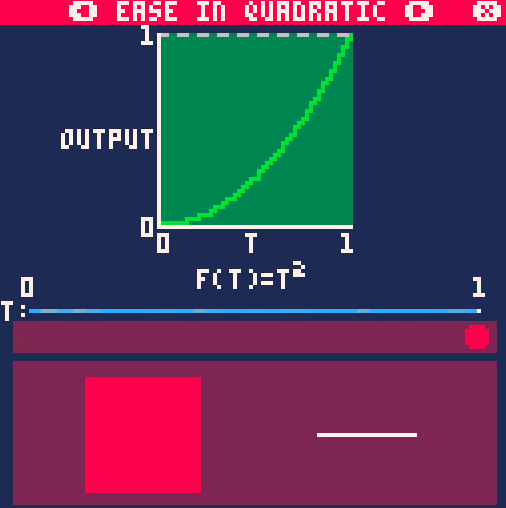
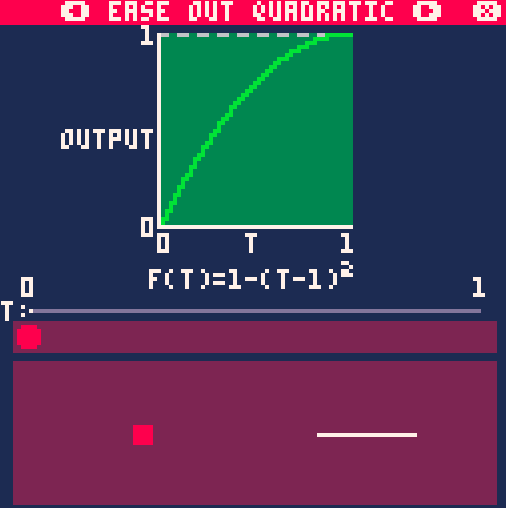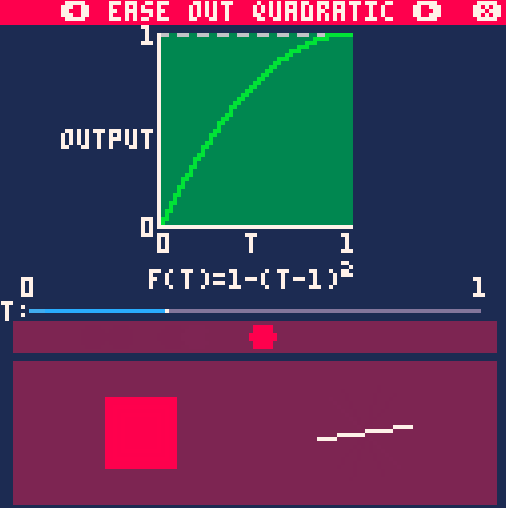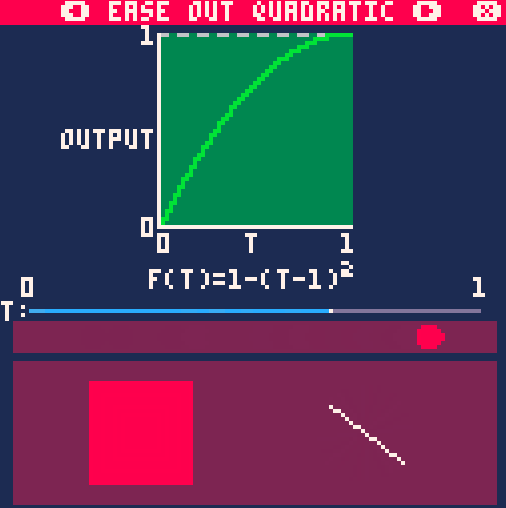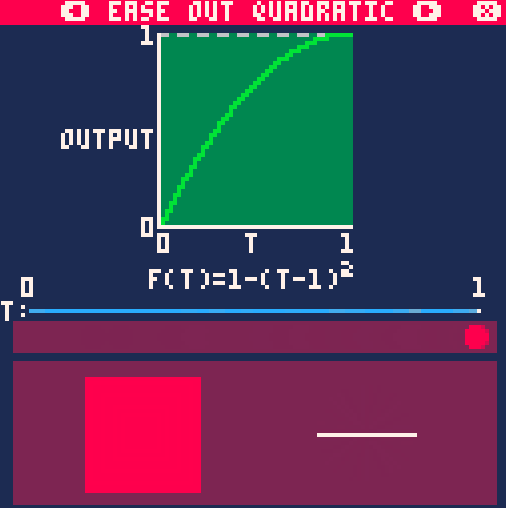
Out-вариант данной функции выглядит так:

float easeOutQuad(float x)
{
	float z = 1 - x;
	return 1 - z * z;
}

Результат:

А это уже совмещение двух предыдущих графиков:

float easeInOutQuad(float x)
{
	if (x < 0.5f)
			return 2.0f * x * x;
	else
	{
			float z = 1 - x;
      return 1 - 2.0f * z * z;
	}
}

Результат:

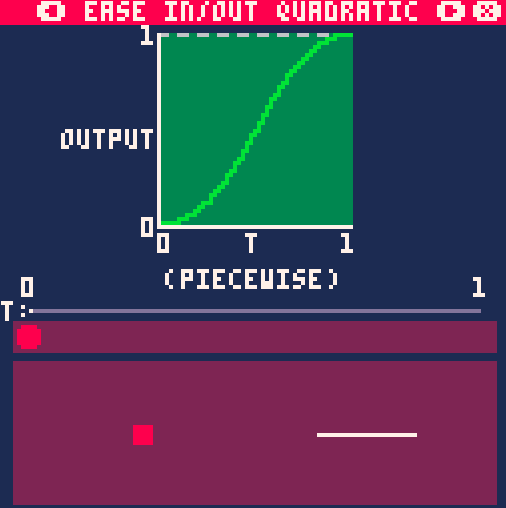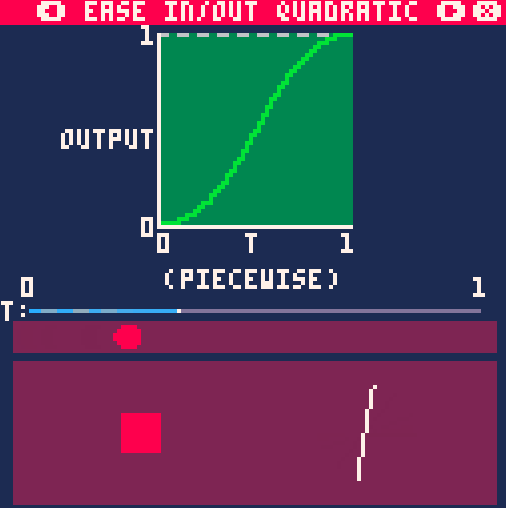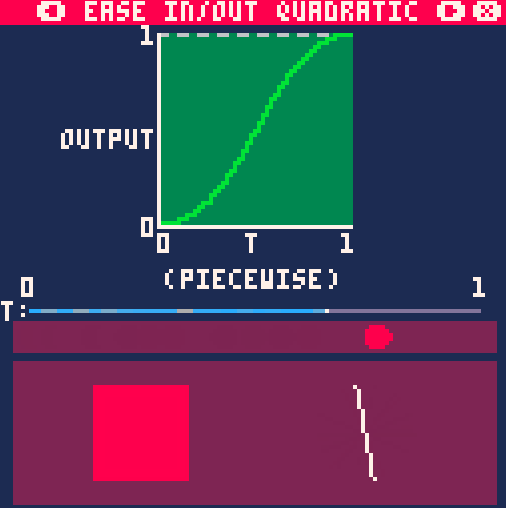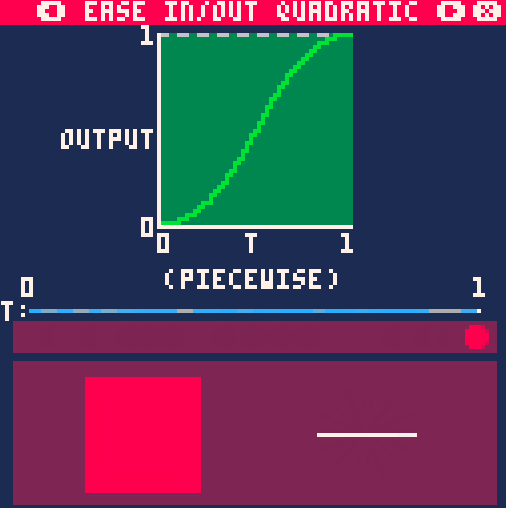
EaseInQuad, EaseInCubic, EaseInQuart, EaseInQuint

//Функция EaseInQuad
float easeInQuad(float x)
{
	return x * x;
}

//Функция EaseInCubic
float easeInCubic(float x)
{
	return x * x * x;
}

//Функция EaseInQuart
float easeInQuart(float x)
{
	return x * x * x * x;
}

//Функция EaseInQuint
float easeInQuint(float x)
{
	return x * x * x * x * x;
}

Как можно увидеть ниже, квадратичная функция (во 2-й степени) — самая плавная, но и самая медленная. А функция в 5-й степени — самая быстрая, но и наименее плавная:

EaseInSine, EaseInExpo, EaseInCirc

//Функция EaseInQuint
float easeInSine(float x)
{
	return 1 - cos((x * PI) / 2);
}

//Функция EaseInExpo
float easeInExpo(float x)
{
	if (x == 0)
		return 0;
	return pow(2, 10 * x - 10);
}

//Функция EaseInCirc
float easeInCirc(float x)
{
	return 1 - sqrt(1 - x * x);
}

А вот как выглядят результаты функций с косинусом, возведением в степень и движением по окружности:

EaseOutBack, EaseOutElastic, EaseOutBounce

float easeOutBack(float x)
{
	const float c1 = 1.70158f;
	const float c3 = c1 + 1;
	const float z = x - 1;
	return 1 + c3 * z*z*z + c1 * z*z;
}

Результат:

float easeOutElastic(float x)
{
	if (x == 0 || x == 1)
			return x;

		const float c4 = (2 * Math.PI) / 3;
		return
			pow(2, -10 * x) *
			sin((x * 10 - 0.75f) * c4) + 1;
}

Результат:

float easeOutBounce(float x)
{
	const float n1 = 7.5625f;
	const float d1 = 2.75f;
	if (x < 1 / d1)
		return n1 * x * x;
	else if (x < 2 / d1)
		return n1 * (x -= 1.5f / d1) * x + 0.75f;
	else if (x < 2.5f / d1)
		return n1 * (x -= 2.25f / d1) * x + 0.9375f;
	else
		return n1 * (x -= 2.625f / d1) * x + 0.984375f;
}

Результат:

Remapping Function

Функции плавности Роберта Пеннера подразумевают, что входной аргумент нормализован (имеет значение от 0 до 1). Выходное значение так же в этих же пределах (почти всегда). Поэтому их часто используют вместе с функцией изменения диапазона:

float remap(float value, float low1, float high1, float low2, float high2)
{
	return low2 + (value - low1) * (high2 - low2) / (high1 - low1);
}

Указываем диапазон, например, от 5 до 10. Если взять число ровно посередине — 7,5, то после изменения диапазона на от 1 до 3 число тоже будет ровно посередине — 2.

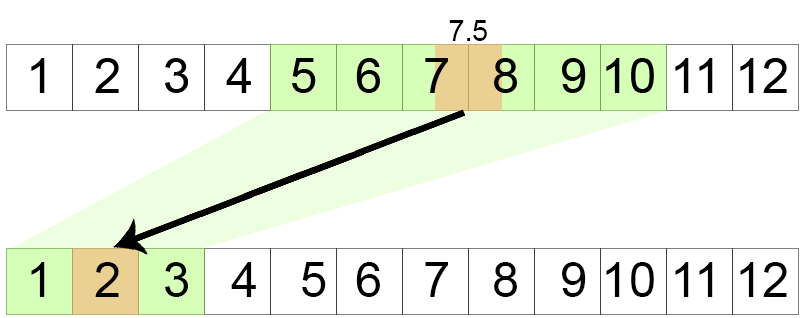
Как работать вместе с easing functions?

Допустим, нам нужна анимация от 5-ой до 7-ой секунды. В этот период надо распахнуть дверь с 0 до 90 градусов:

time_n = saturate(remap(time, 5, 7, 0, 1));
door_angle = remap(easeOutBack(time_n), 0, 1, 0, 90);

Примеры реализации

Функции плавности часто используются в различных интерфейсах, вроде сайтов или мобильных приложений.

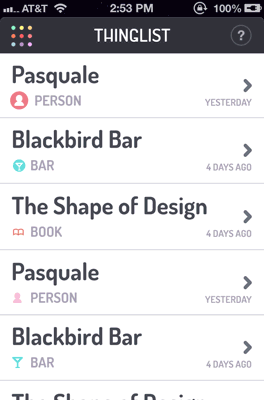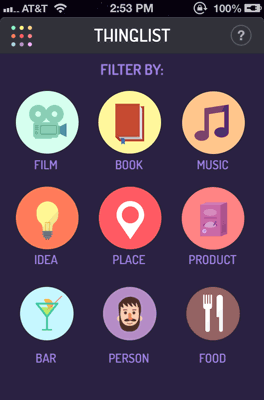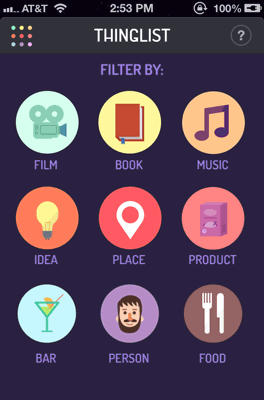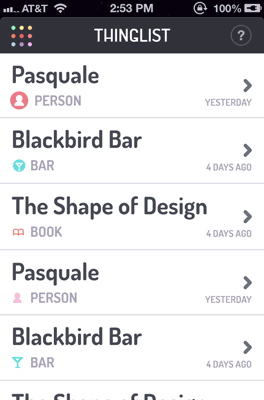
Еще пара Easing Functions

Изначально Роберт Пеннер придумал 30 функций, но позднее разработчикам стало очевидным, что не помешало бы еще что-то. Например, в некоторых ситуациях требуется замедление анимации посередине, а максимальная скорость на краях — так появилась OutIn (вместо привычной InOut):

float easeOutInQuart(float x)
{
	if (x < 0.5f)
	{
		x -= 0.5f
		return 0.5f - 8 * x*x*x*x;
	}
	else
	{
		x -= 0.5f;
		return 0.5f + 8 * x*x*x*x;
	}
}

В результате получаем анимацию, похожую на эффект замедления времени (как в «Матрице»):

А что, если у анимации нет конца?

Такое часто бывает, когда учитывается пользовательский ввод: в интерфейсах приложений или в играх. Например, у нас есть объект, который плавно и постоянно должен двигаться до курсора мыши:

Или скроллинг:

Плавный драг-н-дроп:

Плавная слежка за объектом камерой:

В таких случаях применяются анимации, основанные на физике (physics-based).

А где же взять физику?

Сделать свою!

На самом деле это не так страшно как кажется, потому что кода придется написать ненамного больше, чем было в этом уроке. И как раз в следующем уроке мы и поговорим про создание контролируемых нелинейных анимаций через формулы из физики!