Продолжаем тему модельно-ориентированного проектирования. Ранее мы рассмотрели пример создания «цифрового двойника» для отдельного авиационного теплообменника. В этой статье рассматривается уже авиационная система кондиционирования воздуха и методы создания ее «цифрового двойника», в виде структурной динамической модели.

Для реального модельно-ориентированного проектирования, мы должны иметь модель объекта, на котором мы проверяем работу системы управления максимально приближенно к реальной. Основной вопрос, на который мы пытаемся ответить, каким образом обеспечить соответствие модели и реальному техническому объекту.
Далее под катом:
Рассматриваются проблемы обеспечения точности расчета и скорости вычислений при создании достоверной математической модели реальной технической системы методами структурного моделирования для цифровых двойников. Описывается опыт создания достоверной модели стенда системы кондиционирования воздуха (СКВ). Даются примеры методик достижения необходимой точности модели для разных типов агрегатов системы.
1. Постановка задачи
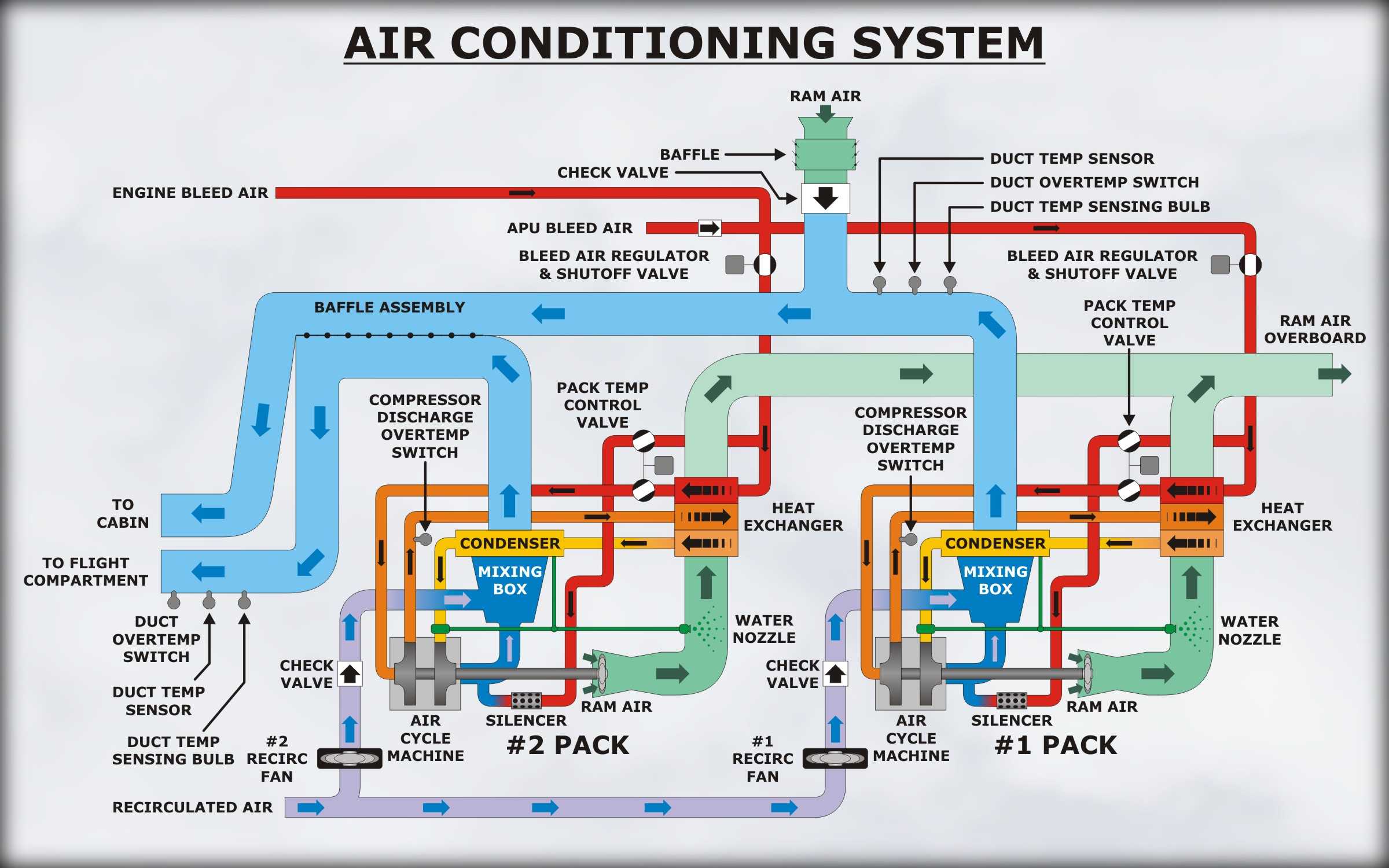
Система кондиционирования воздуха (СКВ) в авиации является важной системой, обеспечивающий температурный режим внутри летательного аппарата. Она содержит как набор теплообменного оборудования, так и систему управления, выполненную с использованием программируемых контроллеров, и состоящую из локальных систем управления агрегатами и общей системы управления, которая должна обеспечивать связь с общей системой управления самолетом.
Работа системы кондиционирования воздуха ЛА обеспечивается забором воздуха из окружающего пространства и его температурной подготовкой. В условиях эксплуатации системы температура воздуха может меняться от +40 °С до – 50 °С (градусов Цельсия). Для обеспечения таких диапазонов температур воздуха при испытаниях системы на земле необходимо дорогостоящее оборудование подготовки воздуха, обеспечивающее охлаждение и снижение давления воздуха для имитации высотного полета.
Создание математической модели стенда испытаний, обеспечивающей достоверный расчет процессов в системе, позволяет значительно улучшить процессы проектирования и повысить качество проектируемых систем с одновременным снижением общей стоимости проектирования испытаний и отладки на аппаратуре.
Наличие достоверной модели позволяет оптимизировать программное обеспечение в аппаратуре управления без проведения дорогостоящего испытания оборудования. А так же позволяет проводить полунатурные испытания аппаратуры управления, когда реальная система управления подключена к математической модели объекта. В качестве программного средства моделирования используется «Среда динамического моделирования технических систем SimInTech».
1.1 Общая последовательность решения задачи
Модельно ориентированное проектирование позволяет использовать модели на всем жизненном цикле проекта и изделия. Если рассмотреть общий жизненный цикл разработки систем с использованием модельно-ориентированного проектирования, то описываемая, в статье методика относятся к стадии изготовления и испытания отдельных агрегатов и создания систем. Стадии 4 – 5 на рис.1
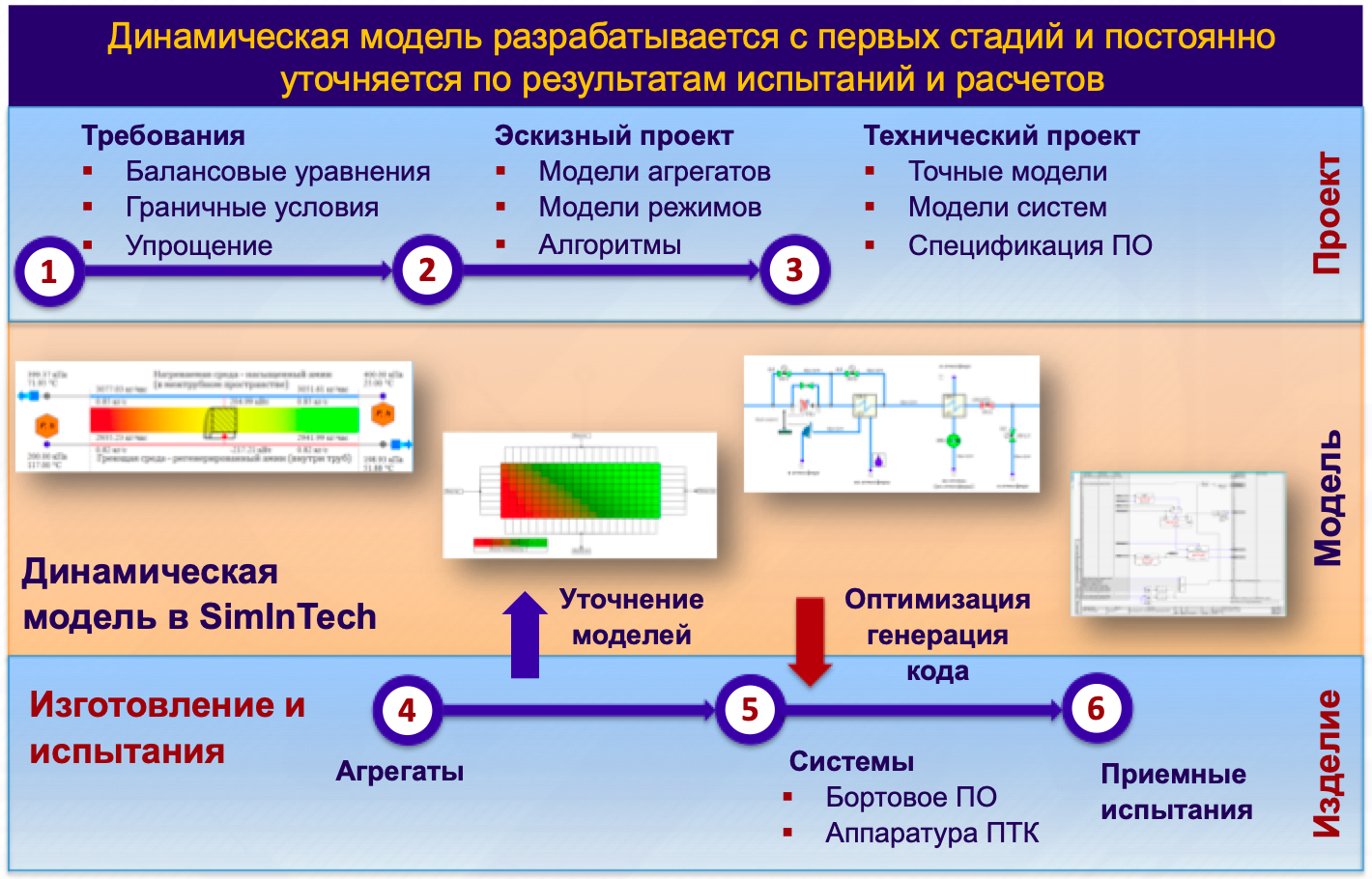 Рисунок 1. Жизненный цикл модели в модельно ориентированном проектирование.
Рисунок 1. Жизненный цикл модели в модельно ориентированном проектирование.
Последовательность создания достоверной модели в SimInTech на стадии между изготовление агрегатов и комплексированием систем общем случае состоит из 3-х основных шагов:
Шаг 1. Разработать алгебро-дифференциальные системы уравнений, описывающие динамическое поведение моделируемой системы.
В среде SimInTech можно задавать уравнения в явном виде (структурные схемы SimInTech и специализированный язык программирования), а также существует большое количество готовых специализированных библиотек для создания моделей, в которых уже предварительно введены основные уравнения физических процессов. В последнем случае пользователь должен только собрать модель в графическом виде и настроить параметры модели.
Шаг 2. Выделить в полученной системе набор эмпирических коэффициентов и характеристик объекта моделирования, которые можно получить из испытаний.
На данном шаге необходимо выявить в модели те свойства, которые не могут быть рассчитаны с достаточной точностью напрямую, но могут быть получены по результатам натурного эксперимента.
Шаг 3. Провести испытания объекта и настроить модель по результатам натурных экспериментов, так чтобы она соответствовала реальности, с нужной степенью детализации. На этом этапе происходит обработка экспериментов и в модель SimInTech вводятся свойства, полученные по результатам этой обработки.
В результате выполнения 3-го шага необходимо добиться, чтобы в виртуальной модели процессы протекали так же как и в реальном объекте. Если это удается, то большую часть экспериментов можно проводить с математической моделью, используя реальный эксперимент только для подтверждения полученных результатов.
1.2 Проблемы достоверности моделей
При создании математических моделей на основе системы дифференциальных уравнений для течения теплоносителя и тепломассообмена необходимо использовать вычисления критериальных зависимостей, которые в общем случае являются зависимыми от геометрии теплообменного оборудования и не могут быть получены из справочников.
В любой реальной системе всегда существуют отклонения и неточности, связанные с допусками при изготовлении агрегата, а также погрешности изготовления, связанные со сборкой компонентов. Для создания цифрового двойника модель должна учитывать эти характеристики реального оборудования.

2. Пример практической реализации процесса
Система кондиционирования воздуха (СКВ) в самолете связана с системой автоматического поддержания давления. Давление в самолете должно быть всегда больше внешнего давления, при этом скорость изменения давления должна находится в безосных пределах. Поэтому система управления притоком и оттоком воздуха является важной для безопасности и для ее разработки на земле ставят дорогостоящие системы испытаний.
Метод структурного моделирования предусматривает разделение модели на подсистемы в соответствии с реальным аппаратным составом моделируемой системы. Система кондиционирования воздуха состоит из нескольких основных типов агрегатов, а именно:
- Теплообменные аппараты;
- Роторные машины (вентиляторы, турбо-холодильная машина);
- Арматура (заслонки, задвижки);
- Контроллеры управления.

2.1 Модель теплообменника
Подробно рассмотрена в этой статье Модельно ориентированное проектирование. Создание достоверной модели, на примере авиационного теплообменника
2.1 Роторные машины
С точки зрения уравнений динамики потока теплоносителя, роторные машины представляют собой дополнительные источники или потребители энергии для уравнения сохранения импульса и уравнений сохранения энергии в рассчитываемом объеме.
Процессы, происходящие в вентиляторах и компрессорах, представляются в виде интерполяционных характеристик объектов, что позволяет использовать методы численного решения дифференциальных алгебраических уравнений, таких же как и для остальных элементов модели. [4]
Структурная схема модели турбохолодильной машины представлена на рисунке 2
.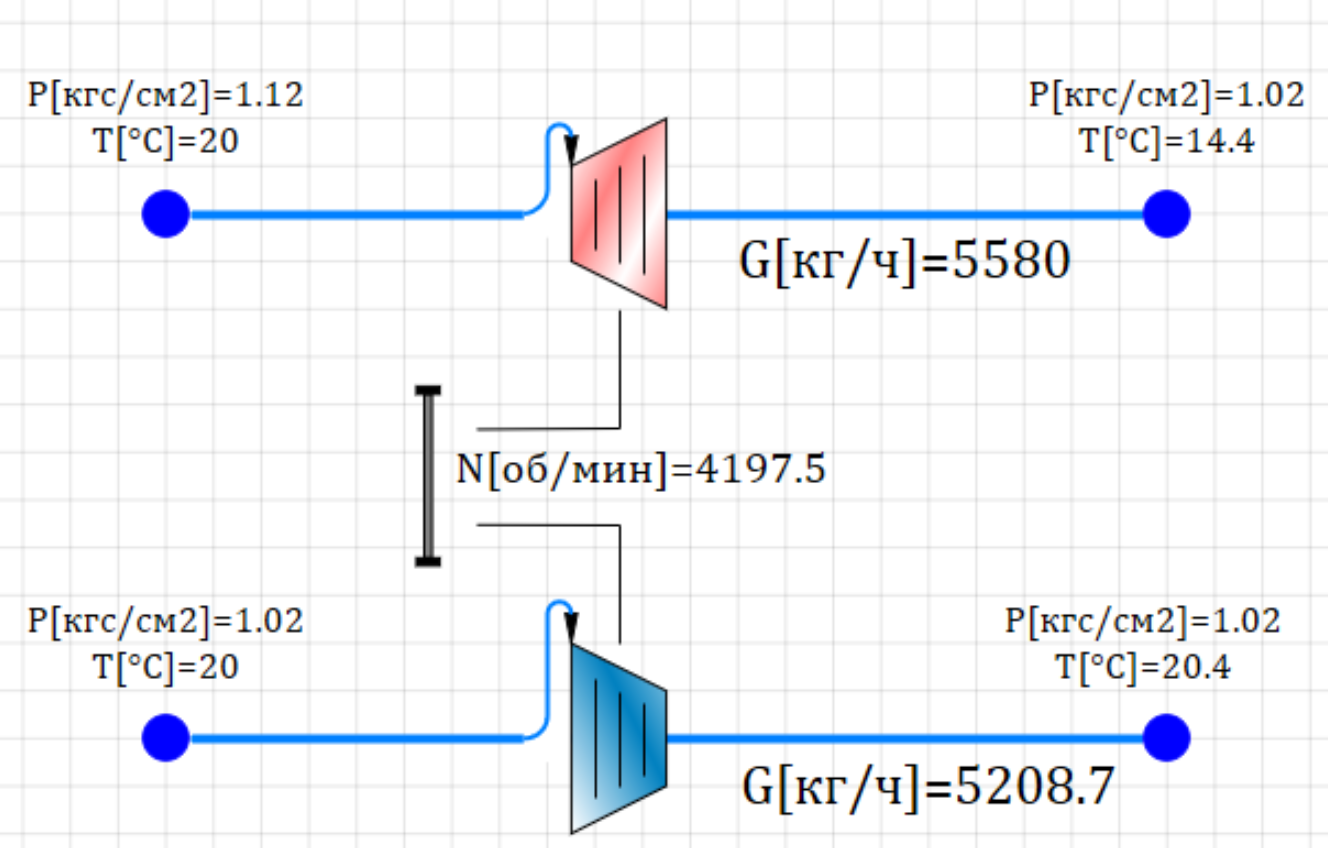 Рисунок 2. Струкутрная схема турбохолодильной машины.
Рисунок 2. Струкутрная схема турбохолодильной машины.
2.2.1 Исходные данные для модели роторных машин
Характеристики для ступеней турбины и компрессора (вентилятора) задаются в табличном виде по сколотым точкам и хранятся в отдельном файле.
Характеристика для ступени турбины задается в виде двух двумерных таблиц:
- зависимость приведенного расхода через турбину от приведенных степени расширения и частоты вращения;
- зависимость КПД от приведенных расхода через турбину и частоты вращения, либо от степени расширения и приведенного расхода через турбину.
Характеристика для ступени компрессора (вентилятора) задается в виде трех двумерных таблиц:
- зависимость степени сжатия от приведенных расхода через компрессор и частоты вращения;
- зависимость КПД от приведенных расхода через компрессор и частоты вращения, либо от степени сжатия и приведенного расхода через компрессор;
- зависимость мощности или момента на валу от приведенных расхода через компрессор и частоты вращения.
Пример характеристики турбины приведен на рисунке 3:
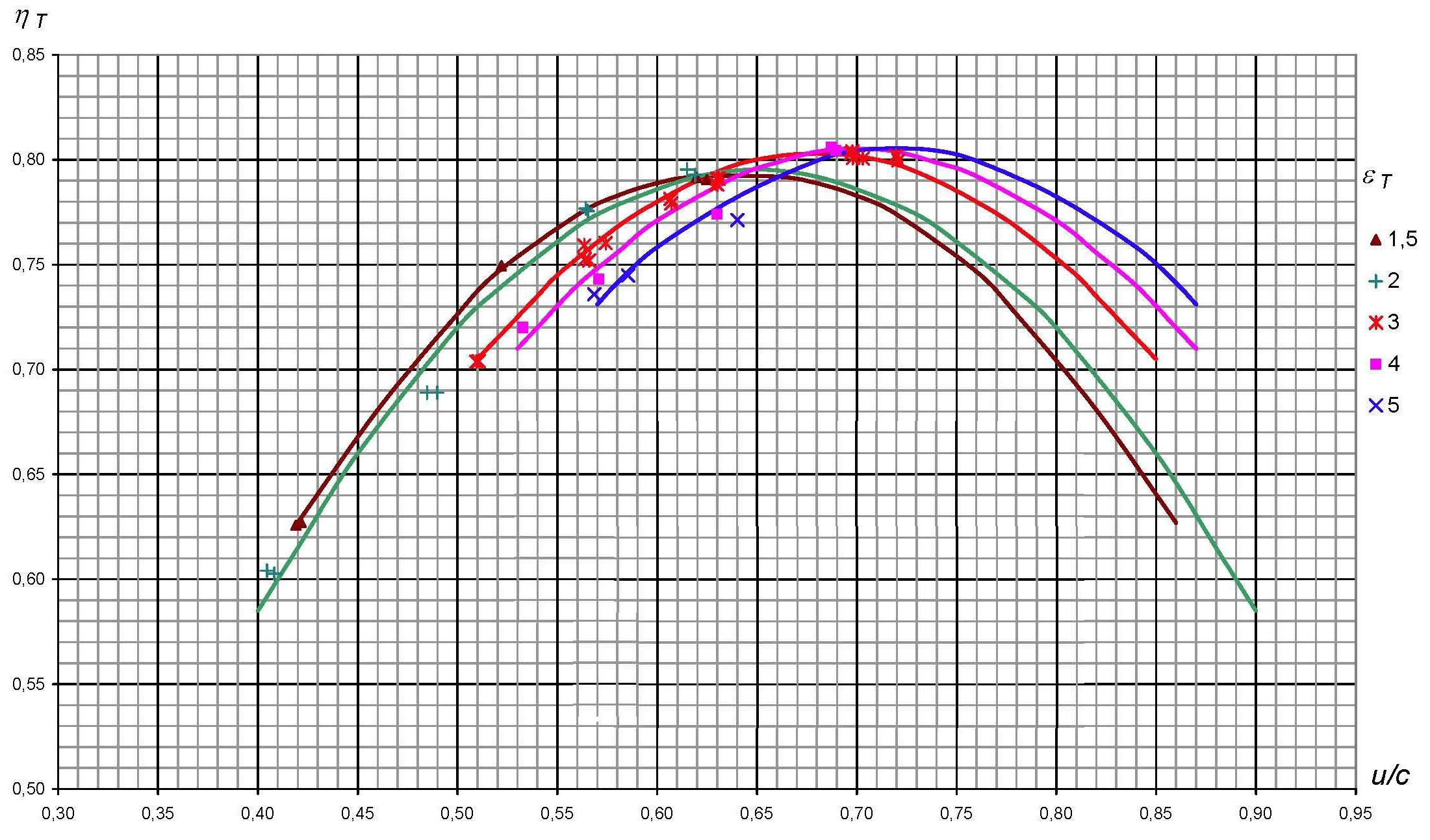
Рисунок 3. Зависимость КПД турбины от приведенных частоты вращения и степени расширения.
2.2.2 Коррекция исходных данных по результатам эксперимента
Как показывает практика, реальные характеристики роторных машин отличаются от заявленных производителем, и данное отличие может существенно влиять на результаты моделирования всей системы в целом. С целью уточнения результатов моделирования в SimInTech разработана методика корректировки характеристик моделей роторных машин. Данная корректировка осуществляет приведение к результатам эксперимента следующих параметров:
- расход,
- частота вращения ротора,
- степень расширения на турбине,
- степень сжатия на компрессоре.
При корректировке соблюдаются следующие правила:
- Низменность форы кривой.
- Диапазон изменения приведенного расхода остается исходным и неизменным для каждой кривой.
- В пределах зоны кривой соответствующий наибольшей частоте вращения ротора, должна иметь наибольшие значение производная приведенной степени сжатия по приведенному расходу.
Сценарий корректировки:
- В качестве исходных данных для корректировки принимаются файл с исходными характеристиками и файл с приведенными параметрами, соответствующими экспериментальным точкам.
- На первом этапе исходная сетка характеристик по обеим координатам дробится: на один шаг сетки добавляется десять новых точек. Промежуточные значения вычисляются бикубической интерполяцией. Это делается для более точного определения корректируемой кривой по первому аргументу (приведенной частоте вращения) и корректируемой точки по второму аргументу (приведенному расходу). Для каждой полученной кривой определяются характерные точки, то есть точки, соответствующие границам зон.
- Определяется зона кривой, куда попала экспериментальная точка.
- В зависимости от определенной ранее зоны происходит сначала корректировка кривой в пределах данной зоны, а затем в пределах остальных зон при условии равенства производных слева и справа на границах зон.
- Данная процедура повторяется для всех экспериментальных точек. Затем скорректированные кривые сравниваются между собой на предмет значения производной в первой зоне. При необходимости происходит повторная корректировка кривых с целью соответствия максимального значения производной функции по второму аргументу (приведенному расходу) в пределах первой зоны максимальной приведенной частоте вращения.
- После окончания работы с кривыми, на которые попали экспериментальные точки, происходит корректировка прочих кривых на основании их начального положения относительно друг друга.
- После корректировки всех кривых характеристики таблицы возвращаются в исходный размер по числу точек по первому аргументу. Затем кривые, которые по какой–либо причине не вписываются в общую тенденцию, убираются из таблицы.
- На завершающем этапе формируются три текстовых файла, в которые записываются соответственно массив значений первого аргумента, массив значений второго аргумента, массив значений функции.
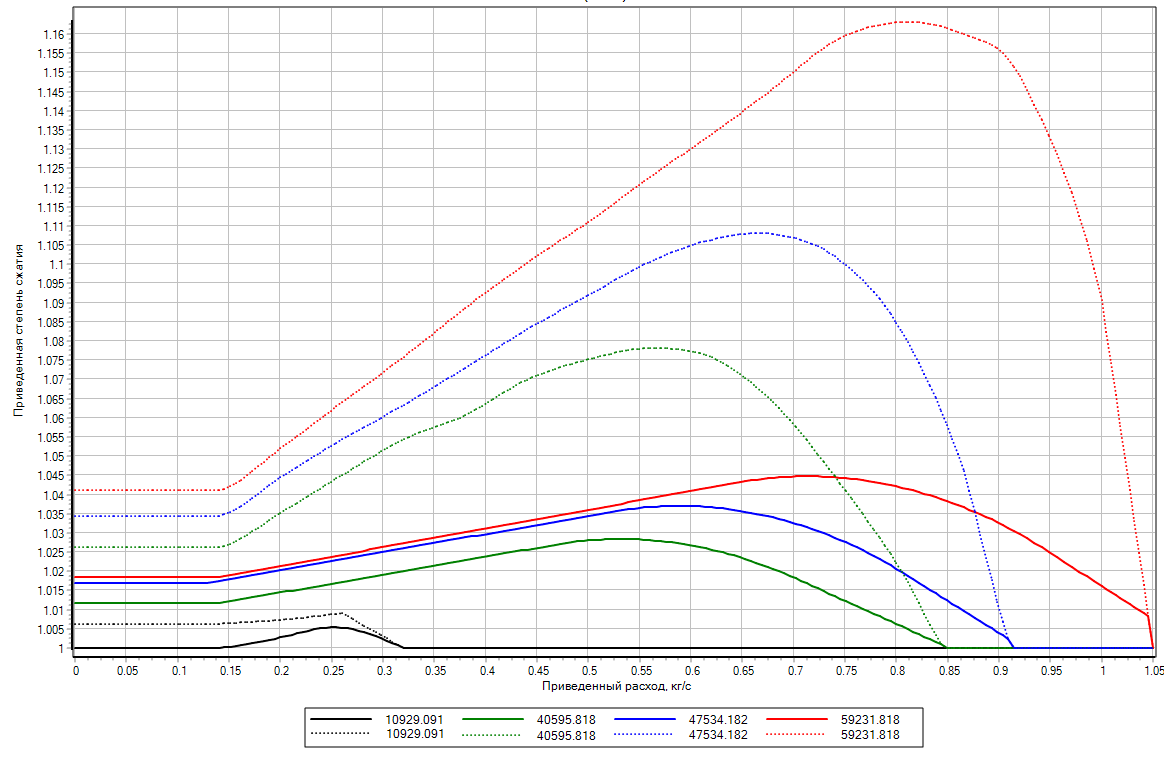 Рисунок 4. Пример напорной характеристики компрессора до и после корректировки.
Рисунок 4. Пример напорной характеристики компрессора до и после корректировки.
После корректировки по нескольким точкам осуществляется проверка результатов моделирования на других точках, не используемых в качестве исходных данных при корректировке характеристик.
 Рисунок 5. Модель для проверки корректировки характеристик турбохолодильной машинки.
Рисунок 5. Модель для проверки корректировки характеристик турбохолодильной машинки.
В таблице 1 приведено сравнение рассчитанных характеристик модели и данных экспериментов до корректировки и после корректировки.
Таблица 4. Сравнение модели турбохолодильника до и после корректировки характеристик.
| Погрешность по отношению к эксперименту, % | ||||||
| Номер эксперимента | Расход через АТ3 по продувочной линии | Частота вращения ротора | Степень расширения на турбине | |||
| Номер эксперимента | До | После | До | После | До | После |
| 1 | 20.2 | 0.5 | 100.0 | 0.9 | 100.0 | 10.2 |
| 2 | 188.5 | 0.2 | 31.1 | 0.4 | 35.1 | 4.1 |
| 3 | 52.8 | 1.3 | 18.9 | 0.7 | 17.3 | 4.4 |
| 4 | 51.8 | 0.8 | 20.0 | 0.3 | 27.8 | 8.7 |
2.3 Запорная и регулирующая арматура
Любая запорная и регулирующая арматура в системе СКВ являются исполнительными механизмами, с помощью которых осуществляется регулирующее воздействие на потоки теплоносителя в системе. Математическая модель арматуры должна обеспечить передачу управляющих воздействий максимально близко к реальному воздействию. Задача осложняется тем, что зачастую в арматуре присутствует набор неопределённостей, связанных с конструктивными особенностями и точностями изготовления.
Математическая модель должна обеспечивать моделирование механических, электрических и программных частей электропривода, при этом обеспечивая достаточную скорость моделирования. [5]
2.3.1 Исходные данные для арматуры
Исходными данными для моделирования арматуры являются:
• расходно-напорная характеристика клапана или заслонки (рис. 6)
• параметры электрического привода (табл. 2)

Рисунок 6. Пример характеристик зависимости расхода от положения.
Таблица 2. Пример характеристики шагового двигателя
| Полный ход штока | 13 мм |
| Шаговый угол | 7.5 град |
| Частота вращения ротора | 100 … 400 Гц |
| Максимальная скорость | 300 шаг/сек |
| Количество шагов | 2625 |
| Полное время хода штока | 8.5 с |
2.3.2 Модель арматуры
Для учета динамики арматуры используется универсальная модель «Блок Управления клапаном» (БУК) в SimInTech.
БУК позволяет реализовать следующие функции:
? управлять электродвигателем клапана из крайних и промежуточных положений;
? останавливать клапан в промежуточном положении;
? открывать/закрывать РК под действием автоматических команд регулятора, дистанционного управления, устройств защит и блокировок;
? выполнять приоритет команд от технологических защит (ТЗ) перед всеми остальными командами;
? запрещать выполнять команды дистанционного открытия/закрытия;
? запрещать выполнять команды открытия/закрытия;
? моделировать набор отказов арматуры.
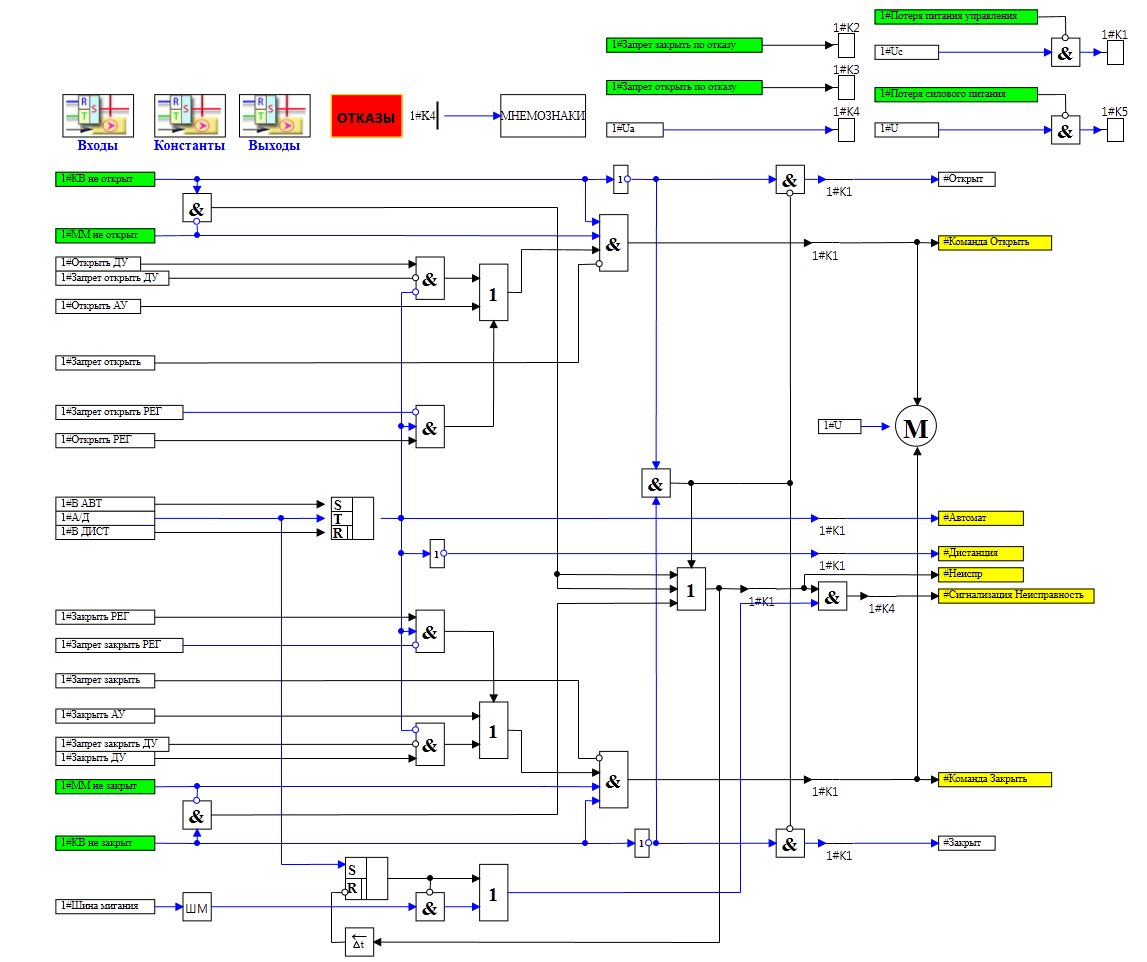
Рисунок 7. Cтрукутурная схема блока управления клапаном.
Блок управления клапаном формирует команду управления, которая передается в исполнительный механизм, в котором происходит вычисление положение штока клапана. При необходимости данный блок формирует отказы, такие как заклинивание, самоход, потеря питания.
В исполнительном механизме происходит моделирование работы шагового двигателя на основании полученных команд, происходит вычисление положения штока клапана с учетом параметров электродвигателя. (см. рис. 8)
Блок управления клапаном формирует команду управления, которая передается в исполнительный механизм, в котором происходит вычисление положение штока клапана. При необходимости данный блок формирует отказы, такие как заклинивание, самоход, потеря питания.
В исполнительном механизме происходит моделирование работы шагового двигателя на основании полученных команд, происходит вычисление положения штока клапана с учетом параметров электродвигателя. (см. рис. 8)

Рисунок 8. Модель исполнительного механизма клапана.
В результате работы модели исполнительного механизма формируется положение штока. В гидравлической модели положение штока пересчитывается в коэффициент относительного сопротивления, который может быть задан по результатам поливки или результатам эксперимента. Данный коэффициент учитывает кривую характеристику, пример которой представлен на рисунке 6.
2.3.4 Настройка модели арматуры
Модель БУК обеспечивает настройку работы модели как с точки зрения гидравлических характеристик клапана, так и работы электропривода. Характеристика конкретного клапана сохраняется в текстовый файл с таблицей, которая может быть легко отредактирована по данным испытаний (рис. 9).
Работа двигателя и механической части системы характеризуется временем открытия–закрытия клапана, а так же наличием люфта и (или) датчиками конечных положений, показания которых используются в системе управления. Настройка данных параметров осуществляется с помощью базы данных сигналов, где эти параметры задаются пользователем и легко могут быть изменены при получении уточненных данных по эксперименту для любого клапана. (рис. 10).
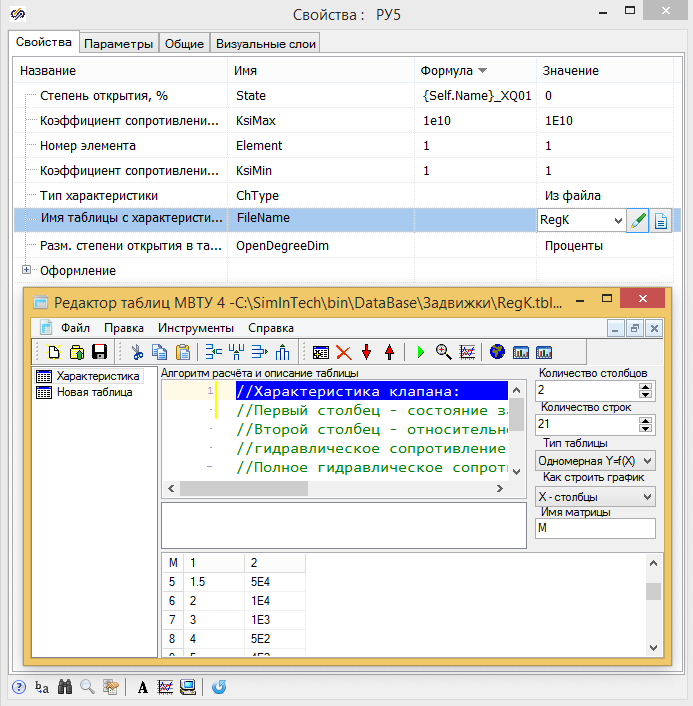
Рисунок 9. Настройка характеристики клапана.
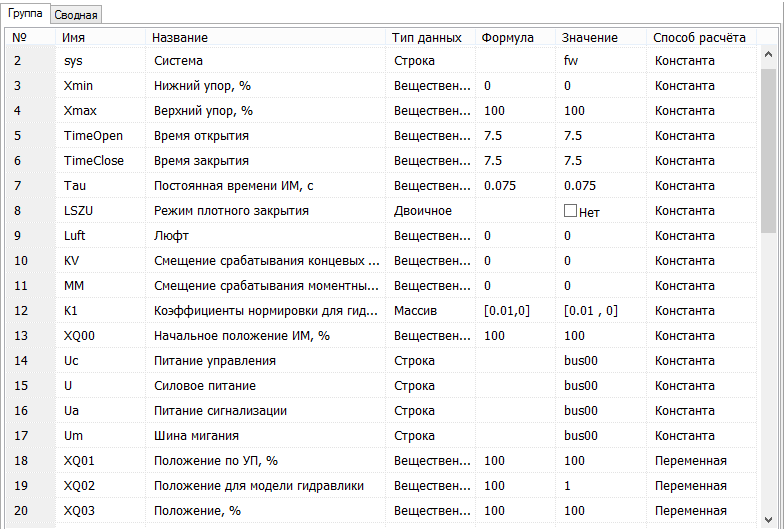
Рисунок 10. Настройка блока БУК.
3. Цифровой двойник виртуального стенда.
После создания и настройки отдельных моделей агрегатов в SimInTech собирается структурная модель всего стенда испытаний.
Общая модель стенда приведена на рисунке 11.
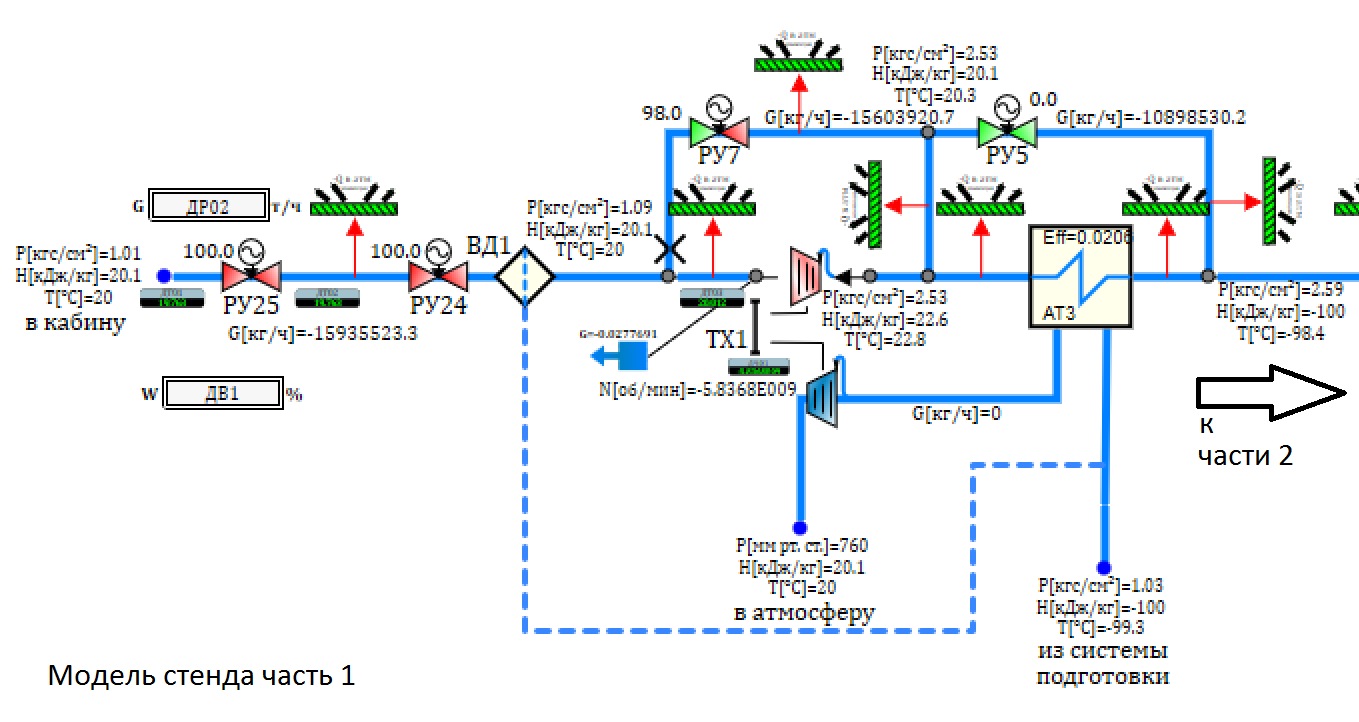

Рисунок 11. Динамическая модель стенда СКВ.
Модель в среде SimInTech сохраняет возможность настройки всех компонентов, входящих в стенд. При изменениях в оборудовании, уточнении его характеристик, или замены компонентов стенда SimInTech позволяет настроить модель по данным реального оборудования для поддержания актуального состояния модели.
Мы получаем цифровой двойник, обеспечивающий расчет процессов со скоростью выше реального времени.
Динамическая модель позволяет проводить моделирование процессов, в том числе для тех режимов, для которых невозможно проводить испытания на стенде, например, моделировать работу с отказами оборудования.
Так же цифровой двойник в среде SimInTech обеспечивает получение дополнительного массива данных по параметрам процессов, физическое измерение которых ограничено конструктивными особенностями реального оборудования стенда. Например, трудность установки датчиков, ограничение габаритов установки, взаимное влияние конструктивных элементов на показание датчиков.
В таблице 3 приведено сравнение интегрального показателя – температуры в кабине для реального стенда и его математической модели в SimInTech для 5 режимов разных режимов работы стенда.
Таблица 3. Сравнение модели и реального стенда
| режим | стенд, °C | модель, °C |
| 1 | 28.0 | 28.9 |
| 2 | 6.3 | 9.7 |
| 3 | 13.7 | 12.6 |
| 4 | 15.4 | 14.1 |
| 5 | 17.3 | 18.5 |
Выводы.
- Структурное моделирование может быть использовано для создания цифровых двойников при моделировании процессов теплообмена в СКВ.
- Предложенная методика обеспечивает настройку цифрового двойника СКВ по результатам испытаний.
- Цифровой двойник в SimInTech позволяет значительно сократить общую стоимость испытаний при одновременном повышении качества проверки проектируемых систем СКВ.
Список литературы.
- Б.А. Карташов, Е.А. Шабаев, О.С. Козлов, А.М. Щекатауров «Среда динамического моделирования технических систем SimInTech» Практикум по моделированию систем автоматического регулирования.
- Сайт Termalinfo.ru Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах. (http://thermalinfo.ru/eto-interesno/kriterialnye-uravneniya-teploobmena-raschet-teplootdachi-v-trubah-i-kanalah).
- М.И. Ведерникова В.С. Таланкин Расчет пластинчатых теплообменников. Методические указания. Уральский государственный лесотехнический университет. Кафедра химической технологии древесины.
(http://elar.usfeu.ru/bitstream/123456789/56/5/Vedernikova_M.I%2C_Talankin_V.S.pdf) - Скворцов Л.М. «Численное решение обыкновенных дифференциальных и диффернециально-алгербраических уравнений»
- Ю.Н. Калачев «SimInTech»: моделирование в электроприводе инструкция по пониманию»


freezlite
> Для реального модельно-ориентированного проектирования, мы должны иметь модель объекта
Я немного сбит с толку, судя по топику речь идет о самолетах, но судя по картинке справа речь о манекенщицах.
petuhoff Автор
О моделях!