Скачать пост в виде документа Mathematica, который содержит весь использованный код, можно здесь.

Одним из самых важных навыков в работе с системой Mathematica, является задание функций, которые имели бы самый разный вид, и зависели бы от разного количества переменных (от буквально ни одной переменной до бесконечного их количества), при этом некоторые переменные могли бы иметь значения, которые используются по умолчанию, если не вводятся их конкретные значения, другие имели бы вид опций, как у многих встроенных в Mathematica функций, или имели бы строгие ограничения на свой тип…

В данном посте будет показано как программировать в Mathematica на русском языке, а для этого я покажу как создать функции, имена которых задаются кириллицей, соответствующие оригинальным встроенным функциям. При этом вы познакомитесь с тем, как собственно задавать самые разные типы и виды функций.

Мне хотелось бы отметить, что в версии 10.1 языка Wolfram Language (Mathematica) начался процесс русификации интерфейса, документации и предсказательного интерфейса. Для ряда языков, например, китайского, процесс полной локализации уже практически завершен. При этом, более того, даже сервис Wolfram|Alpha скоро сможет работать на китайском.

Создание стандартных функций нескольких переменных

Отсроченное задание функции

Задать стандартную функцию можно с помощью конструкции вида:



В данной конструкции участвуют три крайне важных функции Mathematica, первая — это отсроченное присваивание SetDelayed (в короткой форме имеет вид :=), вторая — шаблонное выражение Blank[] (в короткой форме имеет вид _), третья — шаблон с присвоенным ему именем Pattern[name, object] (в короткой форме имеет вид name:object, или, если шаблонный объект представляет собой просто _, то name_).

Рассмотрим подробнее зачем они нужны и как работают.

• Отсроченное присваивание := употребляется в виде:

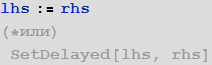
оно присваивает выражение rhs (сокращение от “right hand side” — справа) в качестве отсроченного значения объекта (символа) lhs (сокращение от “left hand side” — слева), при этом выражение rhs остается в невычисленном виде. Как только в коде встречается объект lhs, он заменяется на выражение rhs, которое после этого вычисляется.

• Шаблонное выражение _ употребляется в виде:

или



оно олицетворяет собой любое выражение, написанное на языке Wolfram Language. При этом, шаблон _h задает любое выражение, головная часть которого совпадает с h.

• Шаблон с присвоенным ему именем name_ употребляется в виде:

или



он служит для “передачи” объекта внутри используемых функциональных конструкций (правил замен, задании функций и т. п.)

Что ж, суммируя сказанное выше, можно сказать, что стандартное задание функции одной переменной имеет вид:



которое в полной форме (в той, которой его на самом деле “видит” и использует Mathematica) выглядит так:



Задание функции в виде отсроченного присваивания, которое в общем случае имеет вид:

f[pattern]:=lhs

работает следующим образом:

• как только Mathematica встречает при вычислении кода функцию с именем f, она проводит сопоставление ее вычисленного аргумента expr (если она встретила выражение f[expr]) с шаблоном pattern. В том случае, если выражение-аргумент expr удовлетворяют шаблону pattern, то конструкция f[expr] заменяется на выражение lhs, в котором все символы с именем, соответствующем имени шаблонного выражения pattern заменяются на выражение expr, после чего полученная конструкция вычисляется и замещает исходное выражение f[expr].

Понятно, что если используется задание функции вида f[v_]:=lhs[v], то, как было сказано выше, любое выражение expr удовлетворит шаблону v_.

Приведу пример. Зададим функцию, которая вычисляет :



Попробуем вычислить ее значение от разных аргументов:









Как видно из рассмотренных выше примеров, действительно любой объект (число, символ, картинка) удовлетворяют шаблону x_ и Mathematica легко работает со всеми выражениями, что демонстрирует необычайную гибкость ее языка.

Задание функции многих переменных полностью аналогично. Скажем, зададим функцию 3 переменных:

Создание функции, которая “помнит” свои вычисленные ранее значения

Если изменить отсроченное задание функции следующим образом:



то однажды вычислив значение в некоторой “точке” (значение при некотором значении аргумента, аргументом может быть не обязательно число и необязательно точка в привычном ее понимании...), функция f будет помнить (правда только в рамках данной сессии Mathematica) это значение (здесь была использована функция Set (в короткой форме имеет вид =), которая позволяет присвоить некоторому символу некоторое значение).

Такое задание функции способно сэкономить массу времени, если вычисление правой части отсроченного присваивания функции занимает много времени, но при этом требует больше памяти.

Пример (время вычисления некоторой команды можно узнать с помощью функции Timing):











Из примера видно, что однажды вычислив значение функции в точке, при таком задании функции, в следующий раз оно не займет никакого времени.

• Внимание! Такое присваивание может сыграть с вами злую шутку. Так как значение функции в данной точке хранится в памяти, оно становится нечувствительным к изменению собственно правой части lhs[v] функции:

Абсолютное задание функции

В том случае, если использовать вместо функции SetDelayed (:=) функцию Set (=) в задании функции:



то выражение справа lhs[v] будет вычислено сразу, после чего в него будут подставляться значения аргументов функции при встрече в дальнейшем выражения вида f[expr] в коде. Такая форма задания функции способна сэкономить время в том случае, если вычисление выражения lhs[v] трудоемко и по сути не зависит от конкретного значения аргумента v.

Сравним отсроченное и абсолютное задания функций.

Вычисление выражения lhs[v] не зависит от значения v напрямую:















Вычисление выражения lhs[v] зависит от значения v напрямую:















Из двух примеров выше можно сделать два важных вывода:

• Внимание! Абсолютное задание можно использовать только в том случае, если вычисление конструкции lhs[v] не зависит напрямую от переменной v. Если это не так, то ответ может быть не верен.

• В случае применения абсолютного задания функций, вы получаете возможность заметно ускорить свои вычисления в ситуации, когда вычисление правой части задания функции не зависит напрямую от аргумента.

Задание функции, некоторые аргументы которой имеют значения по умолчанию

В некоторых ситуациях удобно использовать функции, некоторые переменные которых имели бы значения по умолчанию. Задать такого рода переменную для функции можно с помощью функции Optional, которая употребляется следующим образом:



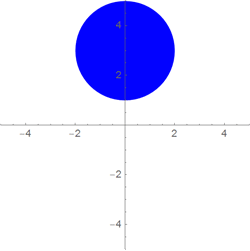
Зададим функцию, которая строит круг или окружность, при этом по умолчанию центр этого круга (окружности) находится в точке (0, 0), он (она) имеет радиус равный 1, а также имеет красный цвет:























Очевидным неудобством работы с такими функциями является то, что если вы хотите использовать много аргументов со значениями по умолчанию, то использовать эти значения у вас получится только в том случае, если они стоят справа от тех аргументов, которым вы придаете какое-то значение. Если же вы меняете какое-то значение по умолчанию на конкретное, то вам придется в обязательном порядке явно указывать и все значения, что стоят левее от него. Таким образом, данное задание очень чувствительно к порядку следования аргументов, а значит переменные со значениями по умолчанию должны располагаться в порядке убыли частоты их использования, если же частота примерно одинакова, то целесообразность задания таких функций резко падает.

Задание функции с опциями

Для того, чтобы избавиться от проблемы, связанной с использованием переменных, которые имеют значения по умолчанию, которая рассматривалась выше, служат функции, которые имеют так называемые опции. Большинство встроенных функции Mathematica имеют те или иные опции.

Для того, чтобы задать опции для некоторой функции, служат встроенные функции OptionsPattern и OptionValue, смысл работы с которыми ясен из следующего примера: реализуем ту же функцию, что и ранее (строящую круг или окружность, с центром по умолчанию в точке (0, 0), радиуса 1, красного цвета), только все значения по умолчанию теперь задаются опциями:

Задание функции с наложенными на аргументы условиями

Для того, чтобы наложить на какой-то аргумент функции ограничение, служит функция Condition (имеющая короткую форму /;).

Скажем, создадим функцию, которая вычислялась бы, только если ее аргумент больше 2:







Или функцию, которая вычислялась бы, если ее аргумент является списком, состоящим не более чем из 4 элементов:







В примере выше также использовался шаблон с указанием головной части выражения List (x_List), который задает любой список.

Такого рода шаблоны могут быть самыми разными:







Также вы можете пользоваться всевозможными тестовыми функциями, которые проверяют, обладает ли выражение, определенным свойством. Это делается с помощью функции PatternTest (имеющая короткую форму ?), стандартный синтаксис которой выглядит следующим образом:



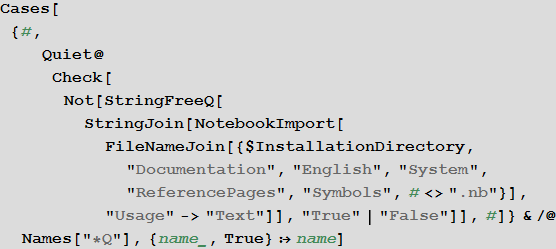
Все тесты (как видно из кода ниже, их 128) в системе Mathematica это функции, которые оканчиваются, как правило, на заглавную букву Q:






128

Скажем, вот так просто можно создать функцию, которая будет работать только с простыми числами:

Альтернативные шаблоны

В некоторых случаях функция должна работать с выражением, если оно удовлетворяет одному из заданных шаблонов. Реализовать подобную конструкцию можно с помощью функции Alternatives (имеющая короткую форму |).

Ниже представлена функция, аргумент которой может быть либо списком, либо целым числом, большим 4:

Множественное задание функций (перегрузка функций)

В Mathematica у вас есть возможность задать определения функции, которые будут применяться в разных ситуациях. Сделать это можно с помощью применения шаблонов с головными частями выражений, а также с использованием ограничений, наложенных на переменные.

В примере ниже создана функция, которая по разному обрабатывает входные данные в зависимости от их типа:

Пример: композиция из описанных ранее способов задания функций и ее аргументов

Программирование в Mathematica на русском языке

Теперь, когда мы знаем о том, как задаются функции, можно поставить перед собой такую задачу: сделать так, чтобы можно было программировать в Mathematica на русском языке с соблюдением основных парадигм: встроенные функции капитализированы и их названия в точности соответствуют действию, которое они осуществляют.

Для этого, нужно сделать русские аналоги встроенных функций.

Начнем с функции Plot, на русском языке ей будет соответствовать функция График. Синтаксис функции Plot имеет вид:



Ее русский аналог будет полностью аналогичен.

Начнем с того, что узнаем список всех опций функции Plot и их значения по умолчанию, это можно сделать с помощью функции Options:





Теперь создадим этот список на русском языке (здесь опущены некоторые опции, которые, по опыту, употребляются крайне редко при построении графика):



Теперь зададим связь русских названий с встроенными аналогами:



Теперь мы можем задать русский аналог функции Plot:



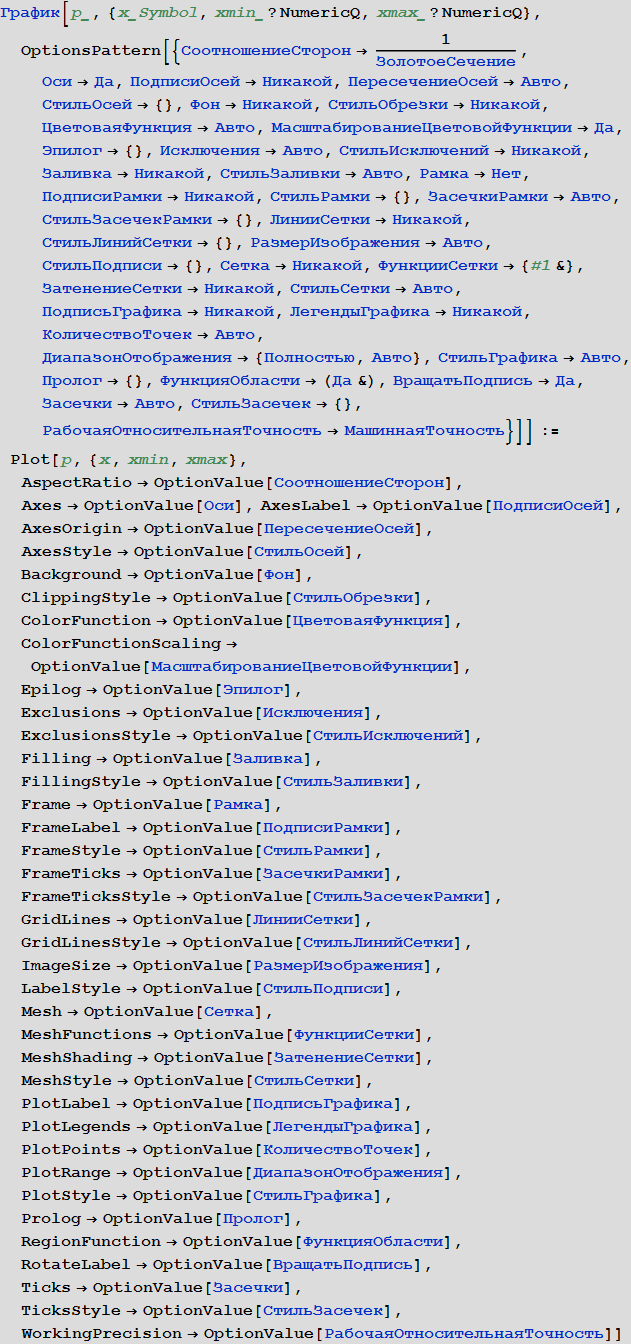
Также нам потребуются некоторые стандартные обозначения толщины и цвета линий:



Аналогично зададим функцию Решить — русский аналог функции Solve, АбсолютныйРазмерТочки — AbsolutePointSize, Точка — Point, Линия — Line:



Попробуем создать некоторый график:









Таким образом, в Mathematica возможно создать пакет, который позволит программировать на обычном русском языке, подобно тому, как это делалось в СССР, скажем на языке АЛМИР-65.

Если у кого-то из вас появится желание развить данную идею, то вполне возможно сделать так, чтобы Mathematica работала на русском языке.